基于全矢1D-CNN的轴承故障诊断研究

谢远东，雷文平，韩 捷

（郑州大学，河南郑州 450001）

0 引言

在旋转机械领域甚至是机械领域，轴承一直被称为机械领域最亮的明珠，广泛应用与机械的各个领域。故轴承故障诊断的研究的成果也直接影响着整个机械领域甚至整个工业化进程的走向。近些年，深度学习和轴承领域的研究也层出不穷，Olivier等人使用卷积神经网络（Convolutional Neural Network，CNN）对于轴承故障的特征进行了提取[1]，李艳峰等人使用Deep Belief Networks 对滚动轴承故障进行研究[2]。使用全矢谱理论对于数据进行特征融合，而后使用1D-CNN 对于轴承故障的特征进行自适应的提取，最后使用Softmax 方法对于故障类别进行判别。该方法在训练的速度、对于故障类别识别的准确率以及模型的泛化性上都表现出很强的竞争性，具有一定的市场前景。

1 卷积神经网络

典型的卷积神经网络的结构分别是输入层、卷积层、池化层或下采样层，以及全连接层，再到最后的输出层。如果只是将卷积神经网络当做特征提取器使用的话，不需要最后的分类层。但如果是做分类任务使用，最后还需要加入分类层。

1.1 卷积层

卷积层的主要操作是对于输入层输入的信号数据进行卷积操作，此卷积非信号处理中的卷积，这里的卷积主要是卷积核也就是多维向量和输入的矩阵的点乘操作然后对于每个点乘的值进行平均得到卷积出的值。具体操作如图1 所示。

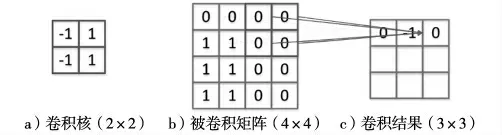
图1 卷积操作

上图是卷积操作，但是对于多通道，例如图像的三通道的数据，需要在3 个通道上同时进行卷积操作。对于故障信号这种单通道数据，只需要进行单层卷积操作即可。假定输入层是第f-1 层，其输入特征图是Xf（heightin×widthin），特征对应的卷积核是K（f）（heightkernel×widthkernel），这样输出维度为：

给每一个输出都加上一个偏置单元（bias term）b（f），卷积层的输出为Z（f）：

其中，χ（i，j）为有效值卷积（Valid Convolution）而非全卷积（Full Convolution）为f 层的激活函数，将在下面具体介绍。

反向传播（Back Propagation）作为参数迭代更新的重要步骤，需要计算残差：

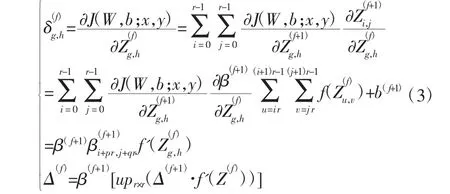
其中，upr×r（X）表示X 在水平和垂直方向复制r 次，目的是将的大小扩大和的相同。并对残差进行求导：

其中，使用χ（u，v）对于上式中的u，v 做了限定，这里的结果为valid 型卷积：

1.2 下采样层

从上一步的卷积后，得到的从输入的数据集中提取到的特征向量，这些特征向量可以指导分类器对于目标进行分类，但在真实的应用场景下，卷积层提取的特征向量维度太大，提取的特征也比较模糊，这是导致模型过拟合一个因素。对于这种情况，可以采用聚合统计，对一定区域中的值进行平均的操作达到降维的目的，把这一个操作叫做池化操作（pool），可以将其分为平均池化（average pooling）和最大值池化（max pooling）（图2）。平均池化的原理就是对一定区域中的值求平均，而最大池化就是对一定区域中的值取最大值操作。根据特征提取时造成损失函数的值很大主要是由于：①池化的范围有限邻域导致最终求得的方差比较大，这种误差对于平均池化可以减少这一类误差；②卷积层参数误差造成估计均值的偏移，最大池化对于这一类误差可以减少，因为对于纹理的削弱能力变差。

以平均池化为例，使用的卷积核每个单元的权重都是β（f），每一项卷积操作后仍然加上一个偏置单元，子采样层的输出为：下采样层同样需要计算残差，如式（3）所示，但是卷积操作为为全卷积操作。

图2 池化操作对比

1.3 全连接层

5 全连接层目前在卷积神经网络同时也是不可或缺的一步，因为全连接层将分布式特征表征映射到样本标记空间，可以大大削弱特征位置对分类的影响因子。因为对于序列信息将会在循环神经网络中提取，所以这时候的信号的位置信息我们将会尽可能的减少提取到上下文关系特征。全连接层对于模型的影响参数为该层的层数、神经元单元个数、激活函数的类型即Sigmoid 或Relu 或tanh 等激活函数。

其中激活函数的作用是增加模型的非线性表达能力。全连接的长度和宽度，理论上神经元个数的增加，模型的复杂度提升；全连接层数加深，模型非线性表达能力提高。理论都能提高模型的学习能力，但是学习能力太好的话，会造成过拟合，并且计算时间会大大增加，造成效率的降低。

2 全矢谱理论

对于双通道采集轴承数据，普遍的做法是将2个传感器放置在互相垂直的位置。但是在实际使用证明，“V”更适合双通道数据（图3）。V 形状的位置设定可以消除传感器重力因素的影响避免提取到噪声特征[4]。

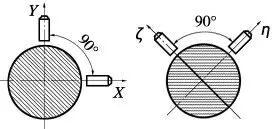
图3 垂直和V 形布置

双通道数据｛xn｝和｛yn｝（n=0，1，2，···N-1），傅里叶变换｛Xk｝和｛Yk｝（k=0，1，2，···N-1），令复序列｛zk｝=｛xk｝+i｛yk｝，其中。通过傅里叶变换得到｛zk｝，并结合正反进动得到以下公式：

其中，Rai为0 主振矢，Rbi为副振矢，αi为主振矢和x 轴的夹角，φi为初相位角。

3 全矢1D-CNN 模型及实验验证

全矢1D-CNN 模型如图4 所示，为一个计算图走向，可以很明显地看出在，左边使用的是循环神经网络中的LSTM（长短记忆网络）模型，在模型的右边使用的是经典的6 层卷积神经网络。其中，前4 层layer1-conv1、layer2-conv2、layer3-conv3、layer-conv4 为网络结构中的卷积操作，后2 层layer5-fc1、layer6-fc2 为全连接层。同时模型伴随着一些超参数以及数据的走向。使用BatchNormalization 对于数据分布不平衡的现象进行中和。这里使用exponential decay 对于学习率逐渐的缩减，和整合拟合过程匹配，避免在接近全局最优解的时候由于学习率过大 而始终无法拟合到极值点。在卷积操作的最后，使用DropOut 技术对于特征向量进行降维，去除掉不重要的特征，不但可以减少计算量，而且可以增加最终模型的泛化性，避免出现过拟合的现象。其中激活函数使用的是Relu（修正线性单元），ReLu 可以使得模型更加的稀疏，稀疏性的同时可以提高模型的训练速度，减少训练时间。

为了进一步验证全矢CRNN（卷积循环神经网络）对于轴承故障判别的优势，使用Center for Intelligent Maintenance at Sinatra University 的滚动轴承全生命周期故障数据[5]。选择2#轴承的全部2156 组数据为正常数据。3#轴承最终出现了内圈故障，对于3#轴承的前1800 组数据标定为正常数据，在1800 到2156 组数据标定为内圈故障。4#轴承最终出现了滚动体故障，对于4#轴承的前1600 组数据标定为正常的轴承数据，在1600 到2156 组数据中标定为滚动体故障。由于每一组数据的维度都是20 480，在经过全矢谱融合后得到的主振矢的维度为10 240，考虑到LSTM 节点数太多会导致计算量急剧增加，并且可能会导致梯度在传递过程中出现消失的现象，确定输入节点数为1024，得到试验样本集。最终数据集的长度为64 680×1024，虽然其中的每个故障类型的数量不一致，但是符合现实情况。

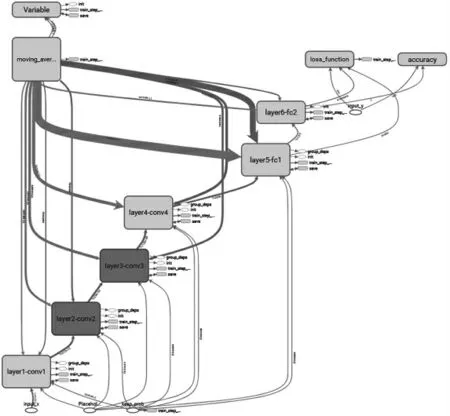
图4 全矢1D-CNN 模型

图5 全矢1D-CNN 模型准确率

为了使实验结果更加严谨，每次从64 680 组样本中随机抽取划分训练集和测试集，一共完成了20 次重复试验。这里取的是在400 epoch 中各模型的最高的测试集上的准确率，消除偶然性的影响。验证集上验证的结果如表1 所示。

表1 试验结果比较（平均准确率±标准差）

由表1 和图5 可知，对于全矢CRNN 来说，在20 次试验中，对于轴承故障的识别率一直稳定在99%左右。而对于单通道的CRNN，例如X 通道CRNN 和Y 通道CRNN 的识别率不但较低，而且会出现抖动的情况，证明其提取的特征的随机性比较大，同时说明该模型的泛化性比较差，即数据集不完备，会确实数据的原始特征，同时也证明了全矢谱对于同源数据的数据完备性的提取可以起很大作用。