智能交通灯控制系统优化*

范姝彤，李思思

（四川师范大学数学科学学院，成都610066）

1 引 言

城市交通控制信号网的基本单位是单叉路口。路口信号灯配时不合理是导致交通不便的主要原因之一。优化路口信号灯的配时可以减少路口拥堵、避免空放，从而提高道路的通行能力。现阶段仅考虑机动车因素的单叉路口红绿灯协调配时方案较多[1-4]。然而，交通的参与形式并非只有机动车一种，仅考虑机动车因素的单叉路口红绿灯配时方案已不能满足人们提升出行效率的要求，尤其在一些行人流量较大的路口，信号灯未考虑行人因素时，会发生诸多违规行为，阻碍机动车通行，大大降低机动车的通行能力。基于此，综合考虑机动车及行人的通行能力和等待时间，建立一个单叉路口实时信号灯配时优化模型。以成都市内静安路川师段交叉口的数据采集为实例，验证所构建模型与算法的有效性。

2 单叉路口车人相位说明

根据机动车及行人在单交叉路口的所有交通流动状态，定义四个相位如表1 所示。其中机动车涉及四个相位，不考虑右转车辆；行人涉及两个相位，与机动车的相位一、三相同。因此把行人的两个相位归于机动车的相位一、三，提及相位一、三时，默认为机动车与人的共同相位。剩余的交通流互相不影响整体的交通情况。

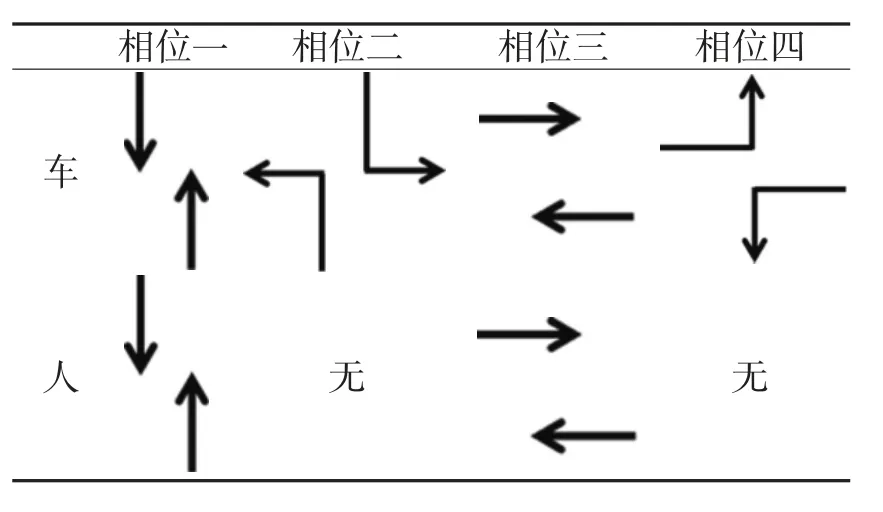
表1 车辆与行人相位说明

3 单叉路口红绿灯实时配时算法

与单叉路口红绿灯实时配时算法有关的主要概念解释如下：

机动车等待时间：一辆机动车从到达单叉路口停下至再次启动的时间；

完全通行时间：在机动车和行人数量一定的情况下，全部机动车和行人通过单叉路口的累积时间；

通车量：在通车时间一定的情况下，通过单叉路口红绿灯的机动车的总数量。

通人量：在通人时间一定的情况下，通过单叉路口红绿灯行人的总数量。

通车率：通车量与通车时间之比；

通人率：通人量与通人时间之比。

算法主要采用一级模糊控制及二级实时控制。首先，根据初始通车率判断选择初始通车相位，接着进入一级模糊控制，计算出此相位的预估模糊通行时间；然后进入二级实时控制，以3s 为一个周期，精确计算出通车率与通人率，进而比较得出下一个通行相位。考虑到机动车及行人的通行安全，在每次变换信号灯前，都设有3s 绿灯闪烁时间和3s 黄灯时间。在3s 黄灯时间内，任何机动车和行人不得进入单叉路口。基于对司机与行人的心理调研，综合设置机动车等待时间最大为120s，若相位等待时间达到120s，则此后优先考虑此相位。

改进的单叉路口红绿灯实时配时算法流程图如图1。在此，选用静安路川师段作为具体讨论的单叉路口实例。考虑行人因素对红绿灯配时的影响，在优化过程中，具体做了如下工作：首先，针对川师南门的实际交通情况，采用抽样调查的方法，统计了一天当中四个时间段，包括8 点、12 点、17 点和24 点的车流量和人流量，用于量化行人对红绿灯配时的影响。接着计算通人率所占总通行率的比例：得到行人因素所占的动态权重系数。权重系数随人流量实时改变，人流量越大，权重系数越大。然后加权计算出未来10s 的总通行量。为计算行人最小安全通行时间，随之抽样调查了静安路川师段老年、青年、少年在行人中所占的比例，加权计算出行人平均速度为1.39m/s，进而计算出最短行人通行时间为15.11s。考虑到3s 黄灯时间，将转换相位后的第一次检测时间增至12s，若检测后不更换相位，则检测时间仍为3s，以保证行人可以安全通过此路口。

图1 改进的单叉路口红绿灯实时配时算法流程图

首先选择初始通车相位。轮流给予机动车的4个相位20s 通车时间，采取视频监控的统计方式，可得出每个相位的初始通车率。从中选择初始通车率最大的相位作为初始通车相位。若存在通车率相同的相位，则任选其一。

接着进入一级模糊配时。通过长时间的视频监测可得到路口各相位的最大通车率及最大通人率通车率最大的相位即为初始通车相位。

表2 初始模糊配时等级

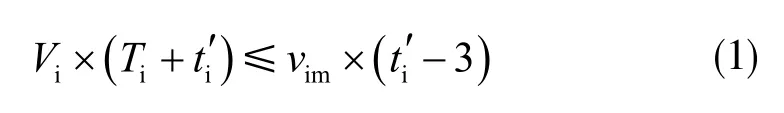
直至到达某个等级终止，此时间即为该相位的初始模糊配时（最长绿灯时间）。其中：Vi表示该相位上一周期通车率；数字3 表示车辆平均启动时间，单位为s。

然后进入二级实时控制。以3s 为周期统计当前相位的通车数及通人数，更新该相位这三秒内的平均通车率和平均通人率，步骤如下[6-8]：

1)计算行人因素所占的动态权重系数，即通人率所占总通行率的比例pi。

2)预测未来10s 各相位的模拟通行率。假设继续给予该相位10s 的绿灯时间，则可计算该相位未来10s 内的通行率为：

进而以同样方法计算其他相位未来10s 通行率Fj。

3)比较Fi和Fj，首先考虑是否有等待时间已经超过120s 的相位，若有，则将该相位作为下一通车相位。

若当前相位的通行率最大，则保持原相位。继续监测下一个3s 周期内的通行率，直至一级模糊配时结束，并把绿灯闪烁之前最后一个周期内的通行率作为该相位的实时通行率。

若存在其他相位的通行率高于当前相位通行率，则将当前绿灯设置为3s 闪烁，再设置3s 黄灯（安全时间），并将模糊通行率最大的相位作为下一通车相位。

若存在通行率相同的相位，则选择等待时间最长的相位作为下一通车相位。

采用完全通行时间作为评价指标，目的是可以更容易与原始的固时情况进行比较。因此，采用控制变量的方法，在机动车和行人数量固定的情况下，以两种配时模型分别得出改进模型和固时情况的完全通行时间。完全通行时间越小，表单通行能力越强，越利于交通通行。

4 模拟结果

固时红绿灯配时方案由图2 所示。可知，对于传统的固定顺序轮转相位红绿灯配时模型，其输入的模拟数据，在一个周期即第一、二、三、四相位轮转一次后可使模拟车辆全部通过，共用时180s。

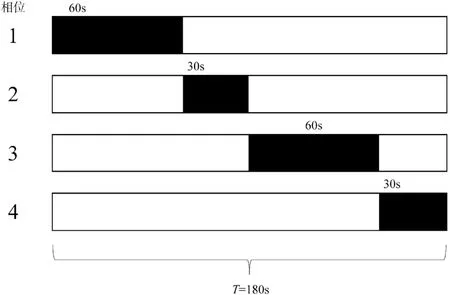
图2 固时红绿灯配时方案示意图

改进实时红绿灯配时方案由图3 所示。对于改进的非固定相位轮转非固时红绿灯配时模型，输入同样的数据，观察其效果变化。

首先给予第一相位15s 通车时间，接着转入第三相位并给予该相位18s 绿灯通行时间，然后转入第二相位并给予该相位24s 绿灯同行时间，依次按图3 所示顺序及时间给予四个相位绿灯通行时间，直至给予第三相位18s 绿灯通行时间可使输入的模拟通车数据全部通过，共用时111s。

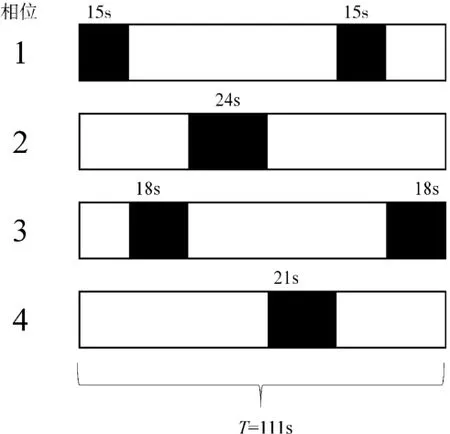
图3 改进实时红绿灯配时方案示意图

接着用上组测试数据在Vissim 软件中进行模拟，改进前后模型的可视化模拟结果分别如图4 和图5 所示。经比较可见，改进模型下，交通拥堵情况有了明显的改善，表明该模型可改善传统固定配时单叉路口的通行能力，有效缓解固时模型的空放问题，提高了通行率。

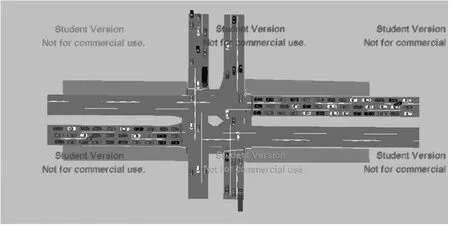
图4 固时模型模拟效果图

图5 改进实时模型模拟效果图

5 结束语

改进后的智能单叉路口红绿灯实时配时算法模型，在对路口交通情况提出合理假设的前提下，充分考虑了路口机动车与行人的通行能力与实际等待时间。故优化后的系统对路口复杂多变的交通情况有很强的适应性，能有效平衡车辆与行人之间的通行需求，更好地满足路口交通信号灯控制的实时性要求。在此基础上，还可提出双叉路口的模型。由于算法仅以单叉路口的实时数据作为依据，各相邻路口之间相互独立，对于双叉路口的情况，可根据实时监测到的通行数据来智能地调控红绿灯配时。此改进算法及模型只是将通人率占总通行率的比例作为行人因素的权重，是否存在更为优化的方案，还需更多的试验及数据来验证。