双向反射分布函数模型的对比分析研究

刘 燕，张 健，吕 瑛

（西北工业大学明德学院信息工程学院，西安710124）

1 引 言

随着航天技术的飞速发展，各国发射入轨的航天器及运载器数量不断增加，而废弃的航天器却绝大多数滞留在轨道上，令近地空间变得越来越拥挤，空间环境问题越来越突出。更令人担忧的是，空间目标与空间碎片数量逐渐增多，相互之间撞击的概率越来越大。在人类航天史上，几次空间碰撞事件的发生都是极小概率、重大问题的体现。2009 年2 月11日。美国“铱-33”移动通信卫星与俄罗斯已废弃的“宇宙-2251”军用通信卫星在西伯利亚北部上空约190km 处当空相撞，巨大的动能使得两颗卫星瞬时化作两团碎片云。这是人类发展航天事业以来，历史上首次发生的两颗整星相撞事件。撞击事件的发生加深了人们对空间安全预警探测问题的关注，引起各国的高度重视[1-2]。获取空间目标信息已变得尤为重要，其中，光学信息获取是最为重要的探测方式。

空间目标光学信息可以由地基或天基的各类光电传感器通过遥感获取。信息的获取主要包括可见光信息、红外信息、光谱信息和偏振信息等。为了分析获取的光度信息，近几年研究人员展开了光度模型的研究，其中基于双向反射分布函数（BRDF）的视星等曲线研究成为热点。在此分析三种常用的BRDF 模型，指出三种模型各自的特点及适用条件，为后续研究空间目标的视星等曲线建立基础。

2 双向反射分布函数

为了表征物体表面光散射的空间分布，1977 年Nicodemus 给出BRDF 的严格定义：经过目标表面反射沿着(θr,r)方向出射的辐亮度dLr(θr,r,Δ)与沿着(θi,i)方向入射到目标表面的辐照度dEi(θi,i)之比。辐亮度定义为：沿着辐射方向单位面积、单位立体角的辐射通量，单位W/(sr·m2)；辐照度定义为：单位面积的辐射通量，单位W/m2。图1 给出了定义BRDF 坐标的几何角度关系，其中θ,分别表示天顶角和方位角，下标i 和r 分别表示入射和探测方向分量。

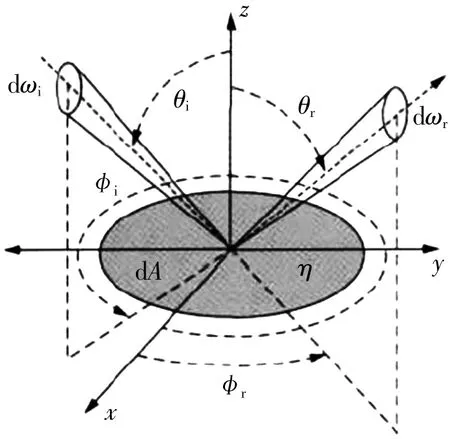
图1 BRDF 几何关系图

BRDF 的一般定义如下式表示：

它是一个微分量，不能直接测；取值范围为零到无限大，单位sr-1。BRDF 表示不同入射角条件下物体表面在任意观测角的反射特性，能够全面反映各种因素对反射辐射的影响。

BRDF 可表示光的一个基本特性，能够全面描述目标的反射光谱在半球空间的分布情况，量化描述不同的入射方向和探测方向的面散射特性和体散射特性的差异。目标表面的面散射特性与表面粗糙度紧密相关，越光滑，镜面反射分量越强，漫反射分量相对较弱。体散射光是由于目标材质不均匀或由不同材质混合而成时，透射光波中一部分经过多次散射、穿过目标表面重新回到大气中而产生的。对于理想的漫反射表面，其标量BRDF 函数与探测几何位置、光源几何位置无关，即BRDF 值不具有方向性，可以利用朗伯表面的BRDF 值ρ/π 代替，其中ρ为反射率，定义为反射辐射通量与入射辐射通量之比。但是自然界中大部分目标表面都不是朗伯表面。因此，出现了很多不同种类的BRDF 模型来描述目标表面的散射特性。

2.1 Torrance-Sparrow 模型

基于镜面反射的微面元理论提出的Torrance-Sparrow 模型目前已经成功应用于遥感探测，用高斯分布作为微面元的概率分布函数[3-4]。微面元理论可简述为：如果目标表面粗糙度大于或等于入射辐射波长，则其可被看成是由一组微面元组成；微面元的法线分布满足某种概率分布，每个微面元的反射特性可近似看成是镜面反射。Torrance-Sparrow 模型的公式如下一组公式所示：

其中，σ 表示物体表面的粗糙程度，其值越小表示物体表面越光滑；下标i 表示入射方向，r 表示观测方向；式(3)中β 为入射方向与zμ间的夹角，=ri为方位角的差；图2 为BRDF 与物体表面法线z 及微面元法线zμ之间的相对位置关系，式(4)中θ 为z与zμ间的夹角，即图2 中的θN；式(5)中PD(σ,θ)为微面元方位（法向）概率分布函数；式(6)中G(θi,θr,)为遮蔽因子。

图2 物体表面法线及微面元法线相对位置关系

2.2 各项异性Phong 模型

各向异性Phong 模型由两部分组成，分别是镜面反射和漫反射[5],如下面公式所示：

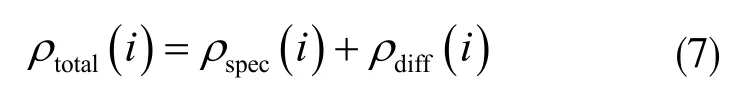
其中，i 表示每个面元。

镜面反射BRDF 可表示为：

式中Rspec为目标材料镜面反射率，上标B 表示目标本体坐标系表示面元指向太阳的单位矢量表示面元指向观测站的单位矢量表示面元指向太阳矢量与指向观测站矢量的平分单位矢量表示面元法线单位向量在面元内且相互垂直，与三者符合笛卡儿坐标系右手定律。

式(8)中，D 为材料镜面反射分布特性，有：

菲涅尔反射为：

式中Rdiff为目标材料漫反射率，漫反射BRDF 即为：

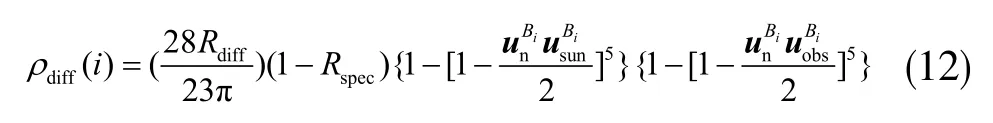
2.3 Davis 模型

Davis 模型如下式所示[6-7]：

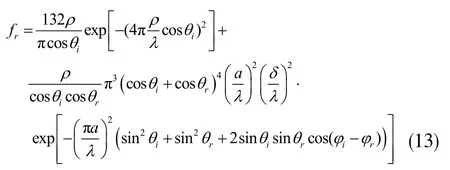
式中ρ 为反射率，λ 为波长，σ 为表面粗糙度均方根；a 为表面自相关长度，入射角为(θi,i)，面元上的出射角则为

3 仿真分析

图3 所示为在观测角θr=30°、方位角=180°时，粗糙度σ 分别取0.1、0.2、0.3 时，Torrance-Sparrow BRDF 模型的值随入射角θi的变化规律，可以看出随着粗糙度的增大，表面的镜面反射分量减小，漫反射特性更加明显。

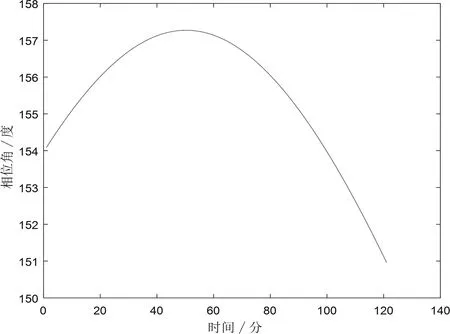
图3 不同粗糙度下BRDF 与入射角的关系

图4 为由各项异性Phong 模型仿真得到的相位角变化曲线图。相位角是指观测矢量和光源入射矢量之间的夹角，它的变化是目标位置变化的结果。各项异性Phong 模型是基于单位矢量表示的，可以通过获取目标、光源和观测点的坐标位置得出相应的单位向量，然后与目标的材料参数，几何尺寸参数以及姿态参数作用以得出目标的光度值。

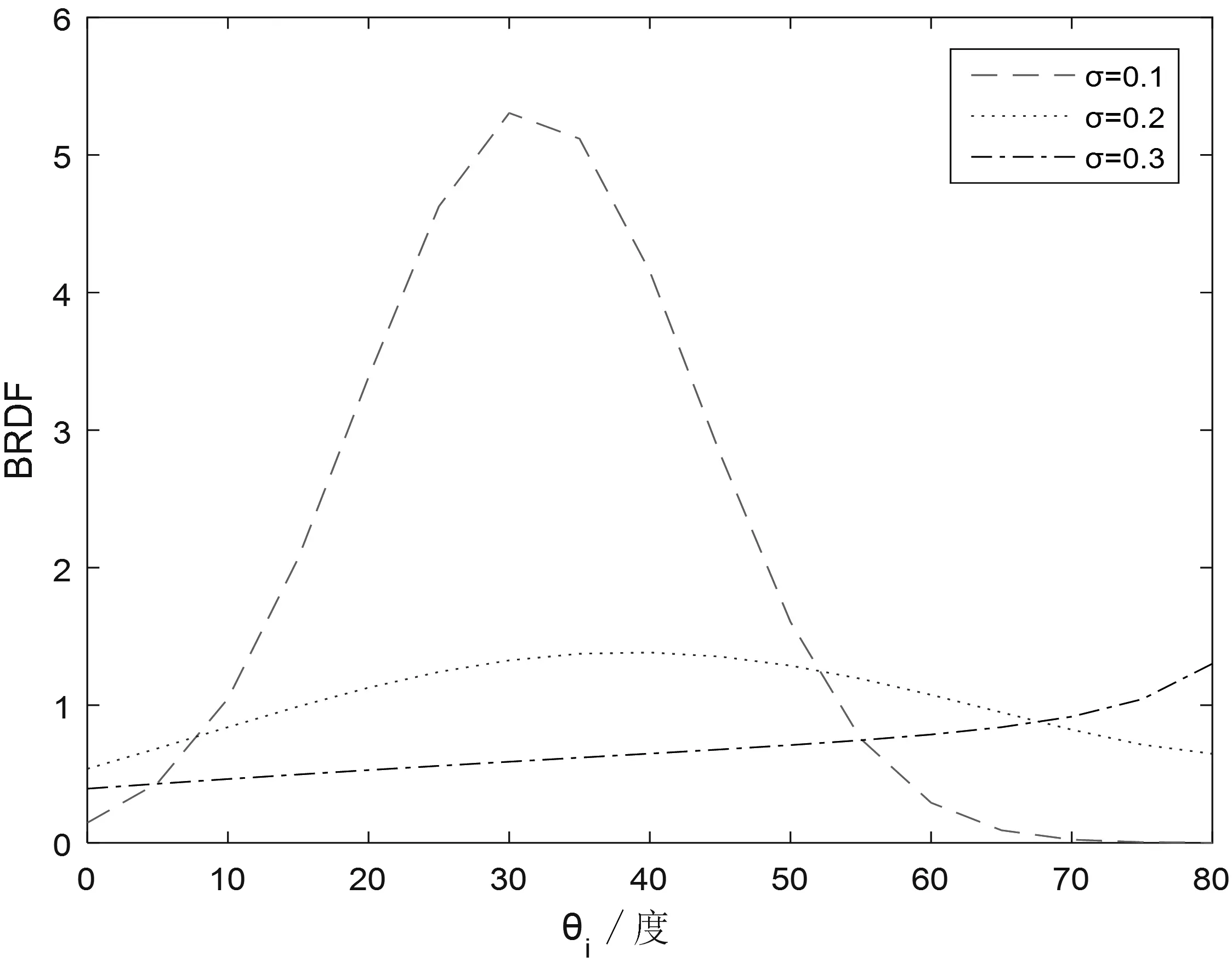
图4 Phong 模型仿真相位角变化曲线

图5 为由Davis 模型仿真得到的BRDF 在可见光波段的光谱曲线图。可以看出BRDF 值随着波长的增加在减小。Davis 模型中有波长参数，可用来分析目标的光谱特性。

综上可见，基于空间目标的光度曲线特点可以反演目标的位置、姿态和大小等特性。空间目标光度特性建模研究成为近几年的研究热点[8-10]。

图5 Davis 模型仿真BRDF 随波长变化曲线

4 结束语

通过分析光度建模中常用的三种BRDF 模型，从仿真分析中得出基于各项异性Phong 模型的相位角随时间变化关系、基于Torrance-Sparrow 模型的BRDF 随入射角变化关系和基于Davis 模型的BRDF 随波长变化关系。三种模型中使用了不同的材料参数，可以根据具体的目标空间位置及目标材料特点选择不同的BRDF 模型。