155 mm固定翼双旋弹二维弹道修正引信的翼面转速特性及修正能力研究
2019-09-11史凯张倩刘马宝
史凯, 张倩, 刘马宝
(1.西安交通大学 航天学院, 陕西 西安 710049;2.陕西华燕航空仪表有限公司, 陕西 汉中 723102;3.金航数码科技有限责任公司, 北京 100028)
0 引言
二维弹道修正引信(CCF)弹道修正技术是一种低成本弹道控制技术,无需新研制弹药,仅将引信更换为弹道修正组件,即可满足大批量库存无控弹药智能化、灵巧化改造的迫切需求,同时还能够减小附带毁伤,使其具有城市作战和对友军火力支持的能力。二维CCF在世界范围内都有广泛研究,各个国家的方案不同,在头部减旋方面基本可以分为整体减旋和翼面减旋两大类,在气动执行机构方面可以分为可动舵片修正CCF和固定翼修正精确制导组件(PGK)。

本文在155 mm口径榴弹平台上对固定翼二维CCF两部分转速特性进行分析,在155 mm榴弹平台上建立双旋运动外弹道模型[11],通过计算流体力学(CFD)软件数值模拟获取翼面部分气动力参数[12]。根据弹丸滚转动力学方程,分别从影响弹丸转速的转动惯量、摩擦力矩、滚转阻尼力矩以及翼面导转力矩几方面对固定翼二维CCF转速、落点、横向偏差、攻角等弹道特性进行分析、对比。结果表明:本文在155 mm榴弹平台所建立的修正翼面模型可以满足二维CCF系统修正能力以及翼面平衡转速要求;仿真分析的双旋弹丸转速规律可代表此类双旋弹丸转速特性。
1 动力学模型
1.1 坐标系介绍
双旋稳定弹分为头部和弹体部分,为了分析双旋稳定弹的转速,首先介绍以下几个坐标系。
1)弹体坐标系。弹体坐标系Oxbybzb以地面坐标系Oxgygzg为基础,先绕Oyg轴转ψ角(偏航角),再绕Ozg轴转动θ角(俯仰角),最后绕Oxg轴转动γ角度(滚转角)。事实上,弹体坐标系Oxbybzb与弹体固连,一般其坐标原点O位于弹体质心位置,其纵轴Oxb与弹轴重合,Oyb轴和Ozb轴指向弹丸径向且相互垂直。
2)准弹体坐标系。由于弹丸绕自转轴高速旋转,如果像一般飞行力学方法将旋转运动投影到弹体坐标系解算,就必须将积分步长取到与弹体高速自转频率相匹配,这样步长就会很小,从而导致计算速度太慢。由于弹丸是轴对称的,可以利用这一特点将弹丸角运动的投影坐标系选为绕Oxg轴转动γ角度的坐标系,称此坐标系为准弹体坐标系Oxbqybqzbq,此坐标系Oxbq轴与弹轴重合,它随弹体做俯仰和偏航运动,但不做滚转运动。
图1中:空速坐标系的x轴与空速同方向,且它绕y轴转βw角(侧滑角),及绕z轴转αw(攻角)后得到准弹体坐标系;βw、αw也是相应于某一攻角αA的两个分量,称αA为全攻角。
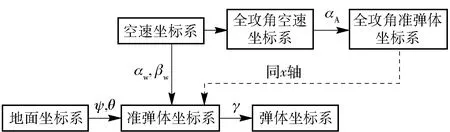
图1 坐标系介绍Fig.1 Coordinate system
值得说明的是,为了模型的建立更加简便和直观,本文弹丸空气动力矩M在全攻角准弹体系内定义,空气阻尼力矩M′在准弹体坐标系定义,弹丸空气动力F在全攻角空速坐标系定义。同时为了描述双旋稳定弹的相对两部分转动,需要重新引入一个坐标系,即头部翼面坐标系。与弹体坐标系相比,头部翼面坐标系的俯仰轴和偏航轴与弹体重合,头部翼面坐标系和弹体坐标系之间仅存在一个滚转角误差Δγ,Δγ=γba-γbf,其中γba和γbf分别为弹体滚转角和头部滚转角。
1.2 绕心运动模型
在准弹体坐标系讨论弹丸绕心运动最方便,而弹体坐标系(头部和弹体)和准弹体坐标系之间仅相差一个滚转角,两个坐标系之间的转换关系如(1)式所示。
(1)
在研究转动时可近似地视地面坐标系为惯性系。设准弹体坐标系相对惯性系的转动角速度为ωq,ωq=[ωqxωqyωqz]T,头部翼面部分质量和弹体质量分别为mbf、mba,在此做一个简化,假设弹体和头部的中心轴与双旋稳定弹的中心轴平行,头部相对于整弹的转动惯量矢量为
(2)
式中:Jbfx、Jbfy、Jbfz分别为头部翼面部分相对x轴、y轴、z轴的转动惯量;rbf为头部翼面部分质心距弹体质心距离。由于弹丸是轴对称,对于准弹体坐标系恒有Jy≡Jz以及所有惯性积为0,Jy、Jz分别为整弹(头部翼面部分和弹体部分)相对y轴、z轴的转动惯量。对弹体而言,转动惯量矢量与头部表达形式一样,仅参数下标ba、bf不同。
根据外弹道力学特性,可以得出弹丸动量矩相对准弹体坐标系的导数:
(3)
式中:H为弹丸相对惯性系的动量矩在准弹体坐标系的投影,为
(4)
则(3)式可以展开为
(5)
式中:Mbfx、Mbfy、Mbfz分别为头部翼面部分所受相对x轴、y轴、z轴的外力矩之和;Mv为弹体对头部产生的阻尼力矩,主要包括轴承摩擦力矩和电磁力矩以及头部自身的滚转阻尼力矩,其中电磁力矩可以人为控制。弹体部分绕心运动模型与上述分析过程一样,可以推导出弹丸头部和弹体部分的转速微分方程为
(6)
式中:ωbfx为头部翼面部分相对x轴的转动角速度;ωbax为弹体相对x轴的转动角速度;Mbay、Mbaz分别为弹体部分所受相对y轴、z轴的合力矩。同时可以得出弹丸转动角度微分方程:
(7)
以上推导出的弹体头部和弹体的转速微分方程、转角微分方程,为双旋稳定弹转速特性分析提供了理论基础。
1.3 作用在弹丸上的力矩
作用在弹丸上的力矩主要由翻转力矩Mz、马格努斯力矩My、滚转阻尼力矩Maxz、俯仰阻尼力矩Mzz. 空气动力矩M在全攻角准弹体系内定义最为方便,此时翻转力矩Mz沿Oz轴,马格努斯力矩My沿Oy轴,其表达式为
(8)
式中:S为弹体的横截面积;d为弹体直径;p为弹体转速;my、mz分别为马格努斯力矩系数导数和翻转力矩系数导数。空气阻尼力矩M′可以直接在准弹体坐标系定义为
(9)
式中:maxz、mzz分别为弹体的滚转阻尼力矩系数和俯仰阻尼力矩系数。由于修正翼面的引入导致弹丸会额外受到翼面所带来的力矩影响,差动翼面引入将会增加导转力矩、滚转阻尼力矩以及轴承摩擦力矩和电磁力矩,其中电磁力矩可以人为控制。在修正机构坐标系中翼面气动力对弹丸力矩MF的影响表达式为
(10)
式中:Mf、Me分别为摩擦力矩和电磁力矩;δy、δz分别为修正翼面相对y轴、z轴的斜置角;xc为翼面压心与弹丸质心沿轴向的距离;CNδ为翼面升力系数。
1.4 作用在引信旋转体上的力矩
作用在引信头部翼面部分旋转力矩:
(11)
式中:l为弹体长度;mfx为翼面导转力矩系数导数;mfxz为滚转阻尼力矩系数导数;摩擦力矩Mf为
(12)
cfx为翼面部分阻力系数,df为引信轴承直径,μf为动摩擦系数;电磁力矩Me此处认为是一常数。则引信头部滚转动力学方程展开式为
(13)
2 翼面部分气动力参数获取
2.1 计算模型及网格划分
155 mm固定翼双旋弹二维CCF弹体外形如图2所示,其中水平的一对翼面是修正翼面,升力方向向上为正;竖直的一对翼面差动安装提供导转力矩为导转翼面。

图2 弹体外形及翼面部分外形Fig.2 Projectile body structure and canard shape
对弹体模型进行三维建模,并对其进行空间非结构网格划分。计算网格由point wise生成,底层边界层网格高度为0.1 mm,最大数量20层,网格量约为590万网格单元,弹体距远场边界大约20倍弹长距离。弹体附近网格示意如图3所示,头部与弹身尾部网格细节如图4所示。本次计算采用软件CFD求解可压缩Navier-Stokes方程,为提高效率采用定常计算,湍流模型为SST模型。
图3 弹体纵切面网格Fig.3 Longitude section of projectile grid
图4 头部翼面部分网格分布Fig.4 Mesh distribution of head canard
2.2 翼面部分气动力参数获取
为了获取翼面的气动特性,分别对来流马赫数Ma分别为0.5、0.8、1.0、1.2、2.0、3.0 6种状态进行数值仿真,得到了翼面导转力矩系数和极阻尼力矩系数;修正翼的气动特性通过对来流Ma数分别为0.5、0.8、1.0、1.2、2.0、3.0 6种状态进行数值仿真,得到了弹丸在0°攻角、8°升力翼面作用下的升力系数。
数值计算结果如表1所示。
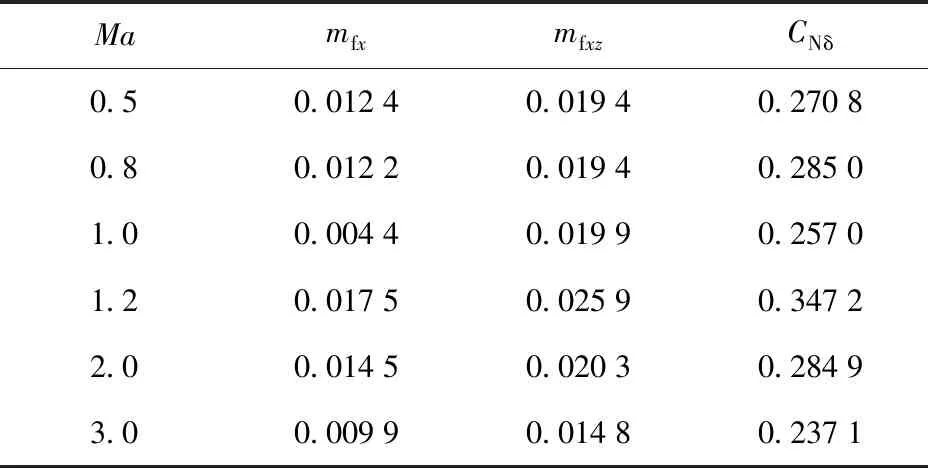
表1 翼面气动力参数
3 双旋弹丸转速仿真分析
通过第1节和第2节的介绍,建立了固定翼二维弹道修正双旋运动模型,获取了翼面部分气动力参数,而弹体部分的气动力参数是通过外场飞行试验雷达数据修正后得到的,本文弹道模型是在155 mm榴弹6自由度(DOF)模型基础下建立的,故可以真实反映实际弹道。图5所示为建立的7-DOF弹道模型与外场试验雷达数据对比,通过对比可以清晰看出仿真弹道模型与实际弹丸弹道基本吻合。
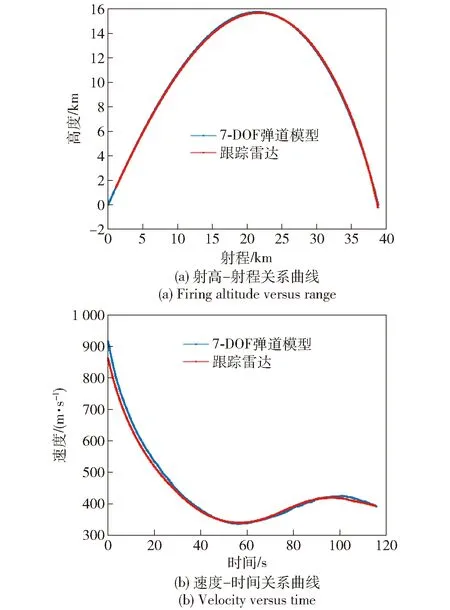
图5 7-DOF弹道模型与跟踪雷达数据对比Fig.5 7-DOF ballistic model compared with radar data
为了更清晰地分析双旋弹转速,根据1.4节滚转通道动力学方程,研究固定翼二维CCF转速特性,假设导转力矩和电磁力矩为0,由(13)式可以看出:引信所受的力矩为滚转阻尼力矩和轴承摩擦力矩;弹丸所受的力矩为滚转阻尼力矩和轴承摩擦力矩。其中翼面的滚转阻尼力矩Mfxz与翼面转速方向相反,弹丸滚转阻尼力矩Maxz与弹丸转速方向相反,轴承摩擦力矩方向始终是阻碍相对运动的。同时可以看出影响头部翼面转速主要影响因素有头部转动惯量Jbfx、滚转阻尼力矩系数导数mfxz、轴承动摩擦系数μf.下面通过仿真对两部分转速进行分析。
3.1 转动惯量对转速影响
为了研究转动惯量对弹丸转速影响,选取仿真平台为155 mm榴弹作为仿真平台,射角52°,初速930 m/s,弹道飞行时间约100 s,出炮口弹丸和翼面部分转速约为300 r/s,此弹道环境与外场炮射试验条件吻合。
为了更好地研究转动惯量对两部分转速的影响,将导转力矩设为0. 即翼面部分仅受滚转阻尼力矩和摩擦力矩作用。仿真情况:导转翼面为0°,修正翼面8°.
从图6中可以看出:当弹体极转动惯量JA与翼面极转动惯量JF比值JA/JF≤1.0时,翼面部分转速比弹丸转速要快;当JA/JF>1.0时随着比值的增加,弹丸转速要比翼面转速快,但是随着比值逐渐增大,翼面部分转速不会一直减小而是最终会逐渐趋于稳定,这与实际弹道飞行环境吻合。
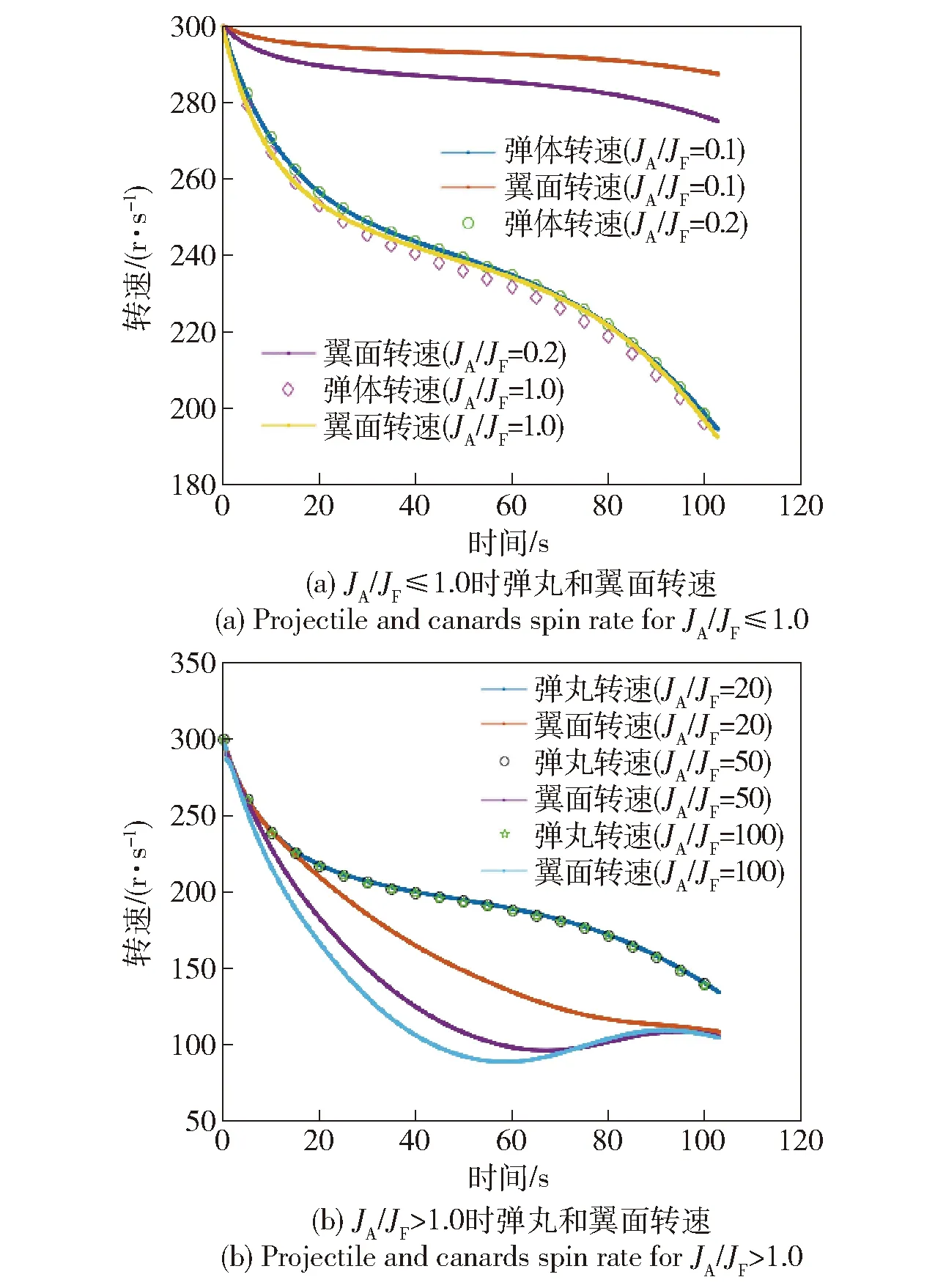
图6 不同JA/JF比值下弹体转速和翼面转速对比Fig.6 Comparison of projectile and canards spin rates for different JA/JF
3.2 转动惯量对弹丸落点影响
从图7中可以看出:当JA/JF≤1.0时弹丸落点横向偏差在JA/JF=0.7时最大;当JA/JF>1.0时弹丸横向偏差随着JA/JF的比值增加逐渐减小,减小的速度是先快、后慢;当JA/JF>100之后横向偏差几乎不变且趋于稳定。

图7 不同JA/JF比值下弹丸落点统计Fig.7 Statistics of impact point at different JA/JF
3.3 转动惯量对弹丸攻角的影响
通过图8中可以看出,随着JA/JF的逐渐增大,全弹道弹丸的攻角最大值逐渐降低,但是降低的幅度不大,全弹道弹丸的飞行稳定性可以保证,全弹道攻角最大值变化趋势可以作为后续头部设计的参考依据。
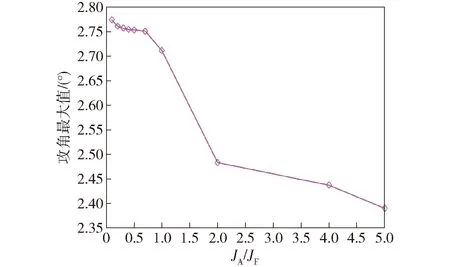
图8 不同JA/JF比值下弹丸攻角统计Fig.8 Statistics of angle of attack for JA/JF
3.4 摩擦力矩对转速影响及滚转阻尼力矩变化
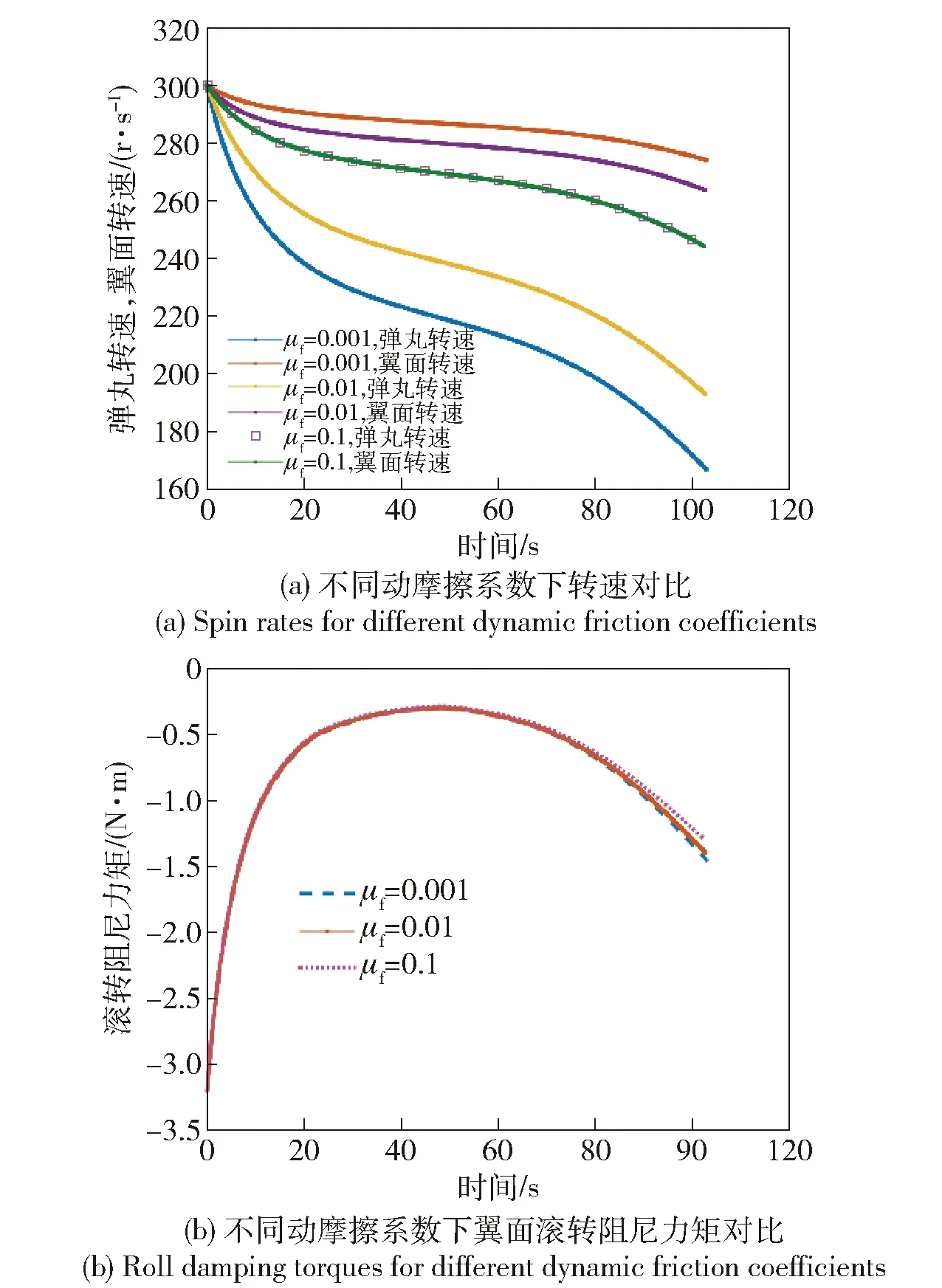
图9 转速对比及翼面滚转阻尼力矩变化(JA/JF=0.3)Fig.9 Variation of spin rate and roll damping torque (JA/JF=0.3)
根据摩擦力矩公式,动摩擦系数选取两个典型例子进行分析:1)JA/JF=0.3即翼面转速快、弹丸转速慢,弹丸及翼面部分转速和翼面滚转阻尼力矩如图9所示。由图9可以看出:随着动摩擦系数的增大,弹丸转速和头部转速差值逐渐减小;当动摩擦系数为0.1时,弹丸转速和翼面转速基本相同,全弹道头部翼面部分的滚转阻尼力矩先减小、后逐渐增大趋于稳定,其中负号代表方向;摩擦力矩在JA/JF=0.3情况下对滚转阻尼力矩影响较小。
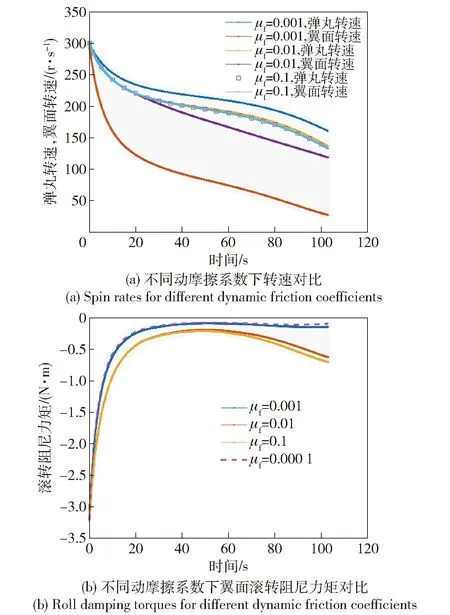
图10 转速对比及滚转阻尼力矩变化(JA/JF=10)Fig.10 Variation of spin rate and roll damping torque (JA/JF=10)
2)JA/JF=10即弹丸转动惯量大时(见图10),全弹道基本弹丸转速高于翼面转速,并且随着动摩擦系数的增大,转速差逐渐缩小。滚转阻尼力矩随着动摩擦系数的降低逐渐减小;随着动摩擦系数降低翼面滚转阻尼力矩不会一直降低,当轴承摩擦系数小于0.000 1时翼面部分滚转阻尼力矩基本保持不变且趋于稳定。
3.5 导转力矩对转速影响
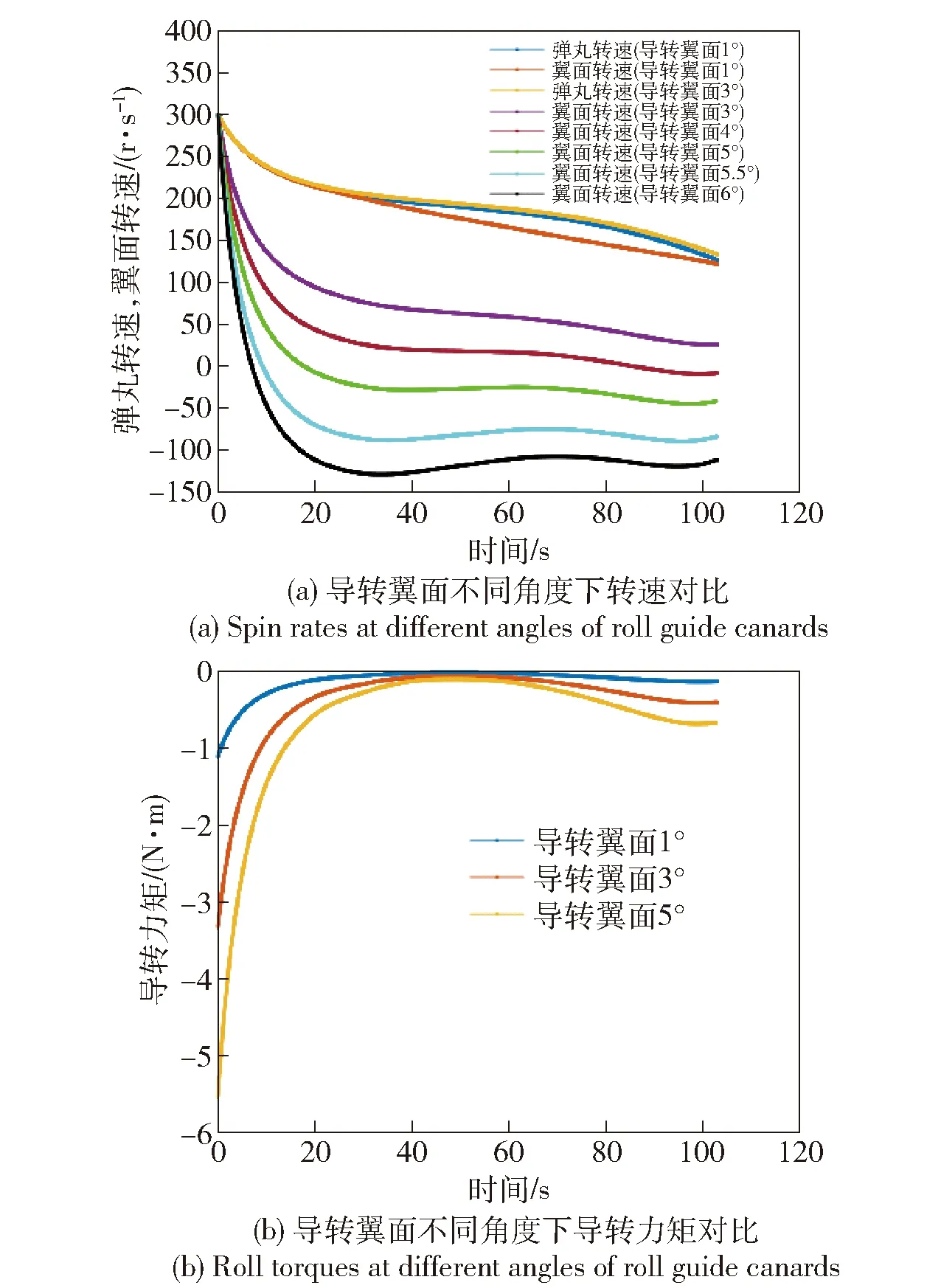
图11 导转翼面不同角度下转速及导转力矩变化Fig.11 Spin rates and roll torques at different angles of roll guide canards
为了验证翼面导转力矩对二维弹道修正转速的影响,根据实际轴承测量得到摩擦力矩系数为0.010 5,转动惯量比值为JA/JF=10. 导转翼面处于不同角度时弹丸及翼面的转速变化如图11所示。从图11中可以看出:随着导转翼面角度的增加,翼面部分转速会逐渐降低;导转翼面4°时翼面相对大地依然向右旋转;当导转翼面5°时翼面转速改变方向,负号代表翼面相对地面坐标系开始向左旋转,最终达到平衡转速约20 r/s;导转翼面5.5°时平衡转速约50 r/s;导转翼面6°时翼面最终达到平衡转速约100 r/s. 同时弹丸转速变化不大,这是因为翼面转速始终比弹丸转速慢,故摩擦力矩方向不变。同时可以看出,随着导转翼面角度的增加,导转力矩一开始是增大的,但是随着时间最终都趋于稳定,最后基本保持不变。
对于固定翼二维CCF设计需要使得翼面相对大地向左转动并维持一定范围的平衡转速,这样磁力矩电机才可以施加合适的力矩从而控制翼面相对于大地静止。根据以上分析可以看出,在155 mm榴弹平台当导转翼面5°~6°时可以保证头部转速相对大地向左,但从仿真结果看当翼面取5.0°~5.5°时翼面的平衡转速范围合理,更有利于后续电磁力矩的施加和控制。
3.6 修正能力分析
根据外弹道理论,弹着点偏离目标偏差由许多因素决定,归纳起来,主要由射弹散布误差和射击系统误差组成。对155 mm榴弹而言,可取射弹散布对应的距离概率误差Exr为1/180,方向概率误差Ezd为1 mil. 距离系统误差的概率误差Exs取为1/240,方向系统误差中测地误差Ezm为1.5 mil,调炮误差Ezg为1.5 mil,射表误差Ezf为1.5 mil. 最大射程Xmax取30 000 m. 综合距离概率误差Ex∑为

(14)
综合方向概率误差为
(15)
因此,距离最大偏差为
ΔX=±4Ex∑=±(4×167)=±668 m,
(16)
方向最大偏差为
ΔZ=±4Ez∑=±(4×87)=±348 m.
(17)
以上即为二维CCF距离和方向修正能力的需求量,二维CCF的修正能力主要由修正翼面斜置角提供的升力来改变弹道,实现对射程和横向偏差方向的修正。以修正翼面斜置角7°、8°、9°计算得到155 mm榴弹的弹道修正能力,取最大射程角52°,修正能力如表2所示。
根据表2以及修正能力需求,当升力面斜置角取8°~9°可满足修正能力要求,但当修正翼面角度继续增大时会使得全弹道攻角变大,弹丸飞行稳定性变差,综上所述,修正翼面角度取8°~9°时可以满足要求。

表2 155 mm固定翼双旋弹二维弹道修正能力
4 结论
本文根据双旋转速和修正能力仿真结果可以得到以下结论:
1)当翼面转动惯量大于弹丸转动惯量时翼面转速高于弹丸转速,同理当翼面转动惯量小于弹丸转动惯量时翼面转速小于弹丸转速,并且随着翼面转动惯量降低翼面转速不会一直降低,最终会趋于稳定。当JA/JF≤1.0时弹丸落点横向偏差在JA/JF=0.7时最大;当JA/JF>1.0时弹丸的横向偏差随着JA/JF的比值增加逐渐减小,并最终趋于稳定;随着JA/JF的逐渐增大,全弹道弹丸的攻角最大值逐渐降低,但不影响全弹道飞行稳定性。
2)当JA/JF≤1.0时随着动摩擦系数的增大,弹丸转速和翼面转速的差值逐渐缩小,当动摩擦系数等于0.1时二者转速基本相同,同时翼面部分的滚转阻尼力矩变化不大;当JA/JF>1.0时随着动摩擦系数的降低,翼面滚转阻尼力矩逐渐降低且最终维持稳定保持不变。上述转速仿真结果不仅为155 mm固定翼双旋弹二维CCF翼面设计提供理论基础,同时仿真得出的双旋弹丸转速规律可代表此类双旋弹丸转速特性。
3)根据实际轴承动摩擦系数和实际转动惯量测定值进行仿真分析,得出:随着导转翼面角度的增大,翼面转速逐渐减小,导转翼面取5.0°~5.5°时翼面的平衡转速范围合理,更有利于后续电磁力矩的施加和控制;同时根据155 mm榴弹的散布和修正能力需求量,对修正翼面不同角度下修正能力进行了评估,在全装药、最大射程角52°条件下,当修正翼面角度取8°~9°时,满足射程和横向散布修正能力要求。
