汽车纵向加速度运动模型分析研究＊

周绍鹏，周金伟，黄玲，杨志勇，游小平

（广东白云学院，广东 广州 510450）

前言

在当今的社会，人们乘坐汽车出行的频率不断增大，生活的各方面与汽车息息相关。汽车在不同路面不平度的道路上行驶时，车辆会持续处于上下振动的状态，这种振动归根结底为汽车纵向加速度的持续变化。当纵向加速度的大小超过人体最适承受范围时，必然会加快驾乘人员疲劳感的到来，使乘坐舒适性降低。汽车乘坐舒适性好坏，主要取决于汽车行驶工况和汽车悬架系统的各项参数等[1]。

本文运用七自由度汽车振动模型，通过理论分析及模拟仿真的方法，研究汽车悬架系统设计参数和路面激励对整车振动特性影响规律，为汽车纵向加速度研究及汽车行驶平顺性的优化设计提供一定理论依据。

1 纵向加速度检测原理

汽车在水平地面静止不动时，三维加速度传感器的x 轴、y 轴和z 轴的加速度均为0 m/s2；汽车在颠簸路面行驶时，传感器z 轴向下加速度（向下为正值）在az≤g（此处g=9.8 m/s2）范围内波动；当汽车车轮完全离地时，传感器z 轴向下加速度az=g，此时的汽车处于完全失重状态，驾乘人员和汽车均被抛起到空中，当汽车下落与地面接触时，由于坠落的冲击力，人体也要承受巨大的反向冲击力，这会造成驾乘人员极大的不适感。

2 七自由度汽车振动模型

汽车是一个复杂的综合系统，汽车正常行驶时，四个车轮受到随机路面激励时，车身产生的各向振动也是非常复杂的。但是，可以简化归纳为车身的垂直振动、侧倾振动和俯仰振动这三类的组合，它们都对汽车纵向加速度有影响。由此可将汽车设为七自由度振动模型，在模型中，4 个车轮可自由上下跳动，车身可在悬架作用下自由振动，则整车的自由度分为4 个车轮的垂向自由度，车身的垂向、俯仰和侧倾自由度，如图4 所示[2]。

图1 七自由度汽车振动模型

图1 中：m1、m2分别表示前轮和后轮质量（kg），m5表示车身总成总质量（kg），Ix、Iy分别表示车身总成绕横轴（x轴）和纵轴（y 轴）的转动惯量（kg.m2），z5表示车身总成质心在纵向方向上的位移（m），z1、z2、z3、z4分别为左前、左后、右前和右后车轮在纵向方向上的位移（m），k1、k2分别表示前、后轮胎的纵向刚度系数（N/m），k5、k6分别表示前、后悬架的刚度系数（N/m），c1、c2分别表示前、后悬架减振器的阻尼系数（N.s/m），q1、q2、q3、q4分别表示路面对左前轮、左后轮、右前轮、右后轮在纵向方向上的位移激励（m），θ 表示车身的俯仰角位移（rad），ψ表示车身的侧倾角位移（rad），a、b 分别表示前、后轴到车身质心的水平距离（m），d 表示汽车左右轮的轮距（m），v 表示汽车行驶速（m/s）。根据七自由度汽车振动模型，运用力学模型对前后车轮和车身分别建立相应的运动微分方程，如式1 所示[2]。

式（1）中，FfL、FrL、FfR、FrR分别表示左前、左后、右前、右后悬架对车身对应连接处的作用力，其表达式如式2 所示：

汽车在实际行驶过程中，车身质量在纵向平面上近似为对称布置，但路面对每个车轮的激励不同。因此，引入七自由度汽车振动模型，它能够明确表达出前、后车轮和车身不同方向的振动受力情况，方便进行车身纵向加速度变化规律的研究。

3 路面激励模型

3.1 空间频率功率谱密度

路面不平度是汽车行驶时的主要激励，通常用数值模拟来替代，可通过测量随机路面数据，经处理运算后，可模拟出路面功率谱密度特性。研究表明，汽车匀速行驶时，路面不平度符合高斯概率分布，表现出零均值的平稳各态特性，遵循以时间为变化参数的随机概率过程，无法用既定的数学函数关系表示[3]。由于速度功率谱为常数，符合白噪声的定义和统计特征，经变换后可拟合出路面随机不平度的时域模型。

现今，我国对汽车振动分析的单位很多，在汽车行驶振动特性研究分析中，以IS0/TC108/SC2N67 国际标准协会提出的“路面不平度表示方法草案”和我国汽车工程研究院制定的“车辆振动输入路面平度表示方法”[4]。以上的两个标准表达的路面不平度都可用公式（3）Gq(n)表示其功率谱密度：式（3）中，n 指空间频率（m-1），与波长λ 互为倒数，即每米长度包含的波长个数；n0指参考空间频率，n0=0.1m-1；Gq(n0)指参考空间频率n0下的路面功率谱密度，也可称作路面不平度系数（m3）；w 为频率指数，即双对数函数坐标上斜线斜率，它决定路面功率谱密度的频率结构[5]。

另外，用σq定义每种响应路面的均方根值，并描述路面随机激励信号的强度或平均功率：

根据以上表示方法的分级标准，按路面功率谱密度把路面的不平度分为8 级，并确定了频率指数w=2 时的各级路面Gq(n0)的几何平均值。同时，确定了当空间频率n 在0.011m-1＜n＜2.83m-1范围内时，路面不平度相应的均方根值σq的几何平均值，如表1 所示[6]。

表1 路面不平度8 级分类标准

3.2 时间频率功率谱密度

按照公式计算需求，将路面不平度的空间频率功率谱密度Gq（n）转化为路面不平度的时间频率功率谱密度Gq（f），当汽车以行驶速度v 驶过空间频率为n 的路面时，等效的时间频率为f。

当车速v 一定时，时间频率f、带宽Δf 分别随空间频率n、带宽Δn 成正比变化。单位频带内的“功率”（均方值）即为功率谱密度。空间频率的功率谱密度可表达为：

为路面功率谱密度在频带Δn 内包含的“功率”。将Δf=vΔn 代入上式，可得空间频率和时间频率谱密度的关系，如公式6 和图2 所示。

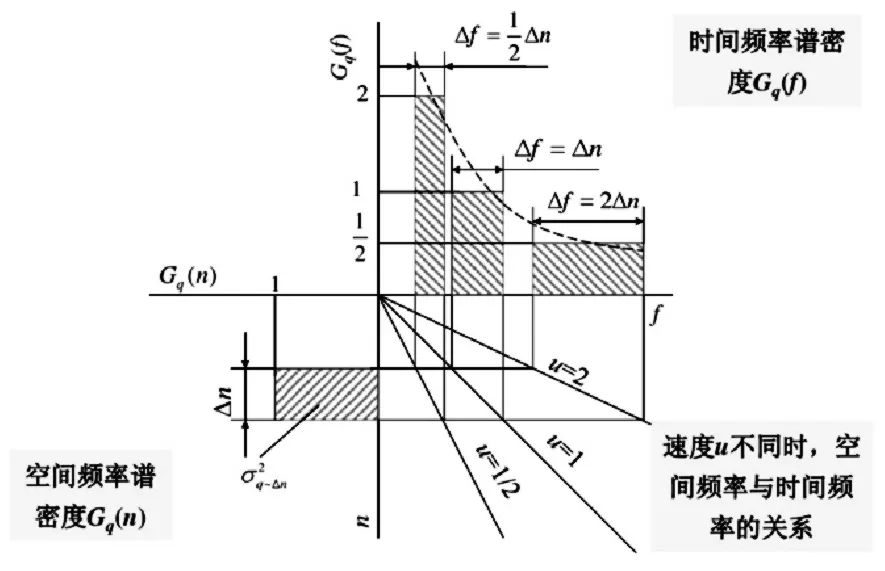
图2 空间频率-时间频率谱密度的关系图

根据公式3、4、6，路面不平度时间频率功率谱密度Gq（f）可用参考空间频率的路面不平度空间频率功率谱密度Gq（n0）、参考空间频率n0、车速v 和时间频率f 表达，其中频率指数w 取为2，转换公式为：

式中，f 为时间频率，f =v·n，Gq（f）即为单轮输入下的位移功率谱密度。

对于七自由度汽车振动模型而言，路面对车轮输入的时间频率功率谱矩阵Gq（f）为：

式中，L 轴距，L =a+b。

假设汽车独立悬架为线性振动系统，根据输入的路面功率谱密度及悬架系统频率响应函数，可求出各振动响应的功率谱和标准差，则可进行车辆垂响加速分析。振动模型中加速度功率谱密度为[7]：

由公式9 可得汽车纵向加速度与路面功率谱密度、路面不平度、汽车速度和时间频率等因素有关，且成正比例关系。

根据我国《公路等级划分标准》、《公路工程技术标准》等相关文件，得出我国公路等级、路面等级和最高限速的对应关系，如表2 所示[7]。

表2 公路等级-限速对应表

为使计算结果更接近汽车行驶时的极限情况，参数选择表2、表3 中的上限值，分别进行高速公路-A 级路面-120Km/h、一级公路-B 级路面-100Km/h、三级公路-E 级路面-60Km/h三种情况的汽车振动模型加速度功率谱密度计算。计算结果如下所示：

高速公路-A 级路面-120Km/h：

以上理论分析结果表明，汽车在三种路面分别以最高限速行驶时，在三级公路-E 级路面以60Km/h 的速度行驶时，车身加速度跳动范围最大，最大值为5.92 m/s2。

4 结束语

本文汽车纵向加速度的理论模型分析和研究得出了以下结论：

（1）汽车以不同速度在不同等级路面上行驶时，车速越快、公路等级越低和路面不平度越大，车身纵向加速度跳动范围越大。

（2）汽车在“三级公路E 级路面-60Km/h”的条件下，车身出现的最大加速度为5.92 m/s2。

（3）本文研究的车身的纵向加速度仅考虑了七自由度振动模型、公路等级和车速等因素，试验模型、典型路面选取不够丰富，研究的结论不够完善。期望课题组后续能够对此项目进行深入研究。