基于改进序列二次规划算法的复杂曲面轮廓度误差评定
2019-09-10马文魁李宁
马文魁 李宁






摘 要:针对复杂曲面的误差评定,本文提出了一种基于改进序列二次规划的误差评定方法,并利用MATLAB软件实现了误差评定的数值模拟仿真计算。实验结果表明,该方法能有效提升復杂曲面轮廓度误差的评定精度,为相关研究工作提供参考。
关键词:复杂曲面;序列二次规划;误差评定;数值仿真
中图分类号:TH161 文献标识码:A 文章编号:1003-5168(2019)22-0050-04
Error Evaluation of Complex Surface Based on Improved
Sequential Quadratic Program Algorithm
MA Wenkui LI Ning
Abstract: Based on improved sequential quadratic program, this paper presented a new method for the error evaluation of complex surface. The numerical simulation calculation of error evaluation is realized by using MATLAB software. Experimental result shows that the proposed method can effectively improve the evaluation accuracy of the contour error of complex surface, which can provide a reference for related research work.
Keywords: complex surface;sequential quadratic program;error evaluation;numerical simulation
随着我国高端制造技术的不断发展和进步,人们对机械产品的制造精度也提出了更高的要求。复杂曲面由于其良好的结构性能,在航空航天、汽车、造船和军工产品等领域具有广泛的应用,甚至对设备的正常运行起到了决定性作用。在复杂曲面零件的加工与检测过程中,高精高效的检测手段与误差评定方法一直以来都是研究人员关注的热点问题,且对衡量产品的加工质量起到了至关重要的作用。
在零件加工质量评定过程中,实测元素相对于图纸规定的理论轮廓和位置所容许的变动量定义为形位公差。国标《形状和位置公差》(GB/T 1182—1996)将形位公差分为形状公差和位置公差两类,其中包括四项形状公差和八项位置公差。针对面轮廓度公差而言,若图纸中标定了基准要求,即认定为位置公差,反之为形状公差。形位公差带主要用于界定实际被测要素的变动区间,即形位误差的最大容许值。若实际被测元素完全包容于公差带内,则认定被测元素合格,反之为不合格[1]。
为了更好地提升复杂曲面误差评定的精度与计算效率,本文重点以无基准要求的曲面轮廓度公差为研究基础,通过对复杂曲面轮廓度误差评定模型的分析,将序列二次规划算法与过滤算法相结合,有效克服了序列二次规划算法的算法缺陷,实现了对复杂曲面零件加工品质高精高效的误差评定。
1 复杂曲面轮廓度误差评定模型
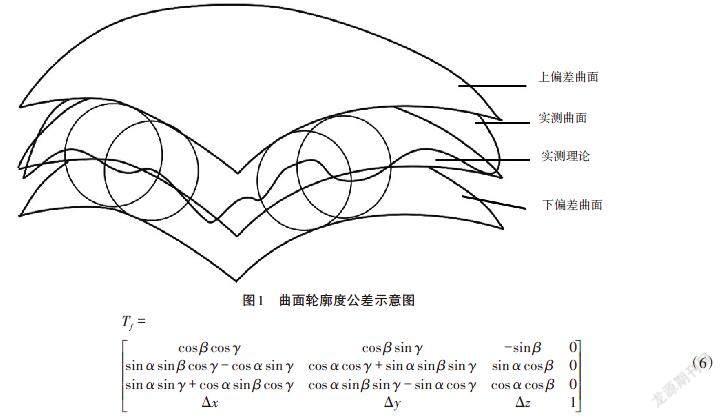
在实际的曲面检测过程中,接触测量和非接触测量是获得曲面三维形貌最主要的两种方法。零件在数控机床加工完成后,一般利用三坐标测量机、扫描仪等工具实现对复杂曲面零件的测量。通过实测要素与理论要素的比对计算,得到曲面轮廓误差,从而实现对零件曲面加工质量的评定。根据ISO[2]标准中的相关定义,复杂曲面轮廓误差的评定是以理论曲面为基础,轮廓度公差为实测曲面在由理论曲面所构成区域内的容许变动量。该变动区域,即公差带是多组直径为公差值,球心位于理论曲面上的球被包容于两包容曲面之间的区域,如图1所示。当实测点完全包容于该区域内,则表示实测曲面符合曲面轮廓度公差要求。
将加工完成后的曲面测点定义为[P=Ph=(xph,yph,zph)h=1,2,……,i],其中[i]为测量点的个数,测量点经过旋转和平移的坐标变换矩阵可表示为:
[Tf=Tp∙Tx∙Ty∙Tz] (1)
式中,[Tp]为测量点的平移坐标变换矩阵;[Tx]、[Ty]和[Tz]分别为测量点绕[X]、[Y]和[Z]轴的旋转坐标变换矩阵。这四个变量分别为:
[Tp=100001000010ΔxΔyΔz1] (2)
[Tx=10000cosαsinα00-sinαcosα00001] (3)
[Ty=cosβ0-sinβ00100sinβ0cosβ00001] (4)
[Tz=cosγsinγ00-sinγcosγ0000100001] (5)
将式(2)至式(5)代入式(1)可得:
经过坐标变换后的测量点坐标[Q=Qh=(xqh,yqh,zqh)h=1,2,……,i]可由式(7)计算获得。
[Q=Tf∙P] (7)
根据ISO[2]误差评定标准引入的最小包容区域原则,应尽量减小实测曲面与理论曲面之间的最大间隙,使其最大间隙最小化。复杂曲面轮廓度误差评定模型建立如下公式:
[e=minmax2d(Δx,Δy,Δz,α,β,γ)] (8)
式中,[d(Δx,Δy,Δz,α,β,γ)]为实测点与理论曲面之间的距离;Δx,Δy和Δz分别表示实测点沿着[X]、[Y]和[Z]轴的平移距离;α,β和γ分别表示实测点绕[X]、[Y]和[Z]轴的旋转角度。
2 误差评定方法
由曲面误差评定模型可以看出,基于最小区域的复杂曲面轮廓度误差评定主要是通过不断调整测量点的空间位置,保证全局测点到理论曲面轮廓的最大距离最小,属于非线性多元参数优化问题。针对公式(8)所建立的曲面轮廓度误差评定模型,若要实现对曲面的误差值的计算,主要需要解决两方面的重点问题:一是测点到复杂曲面距离的计算;二是实测点与理论曲面的最优匹配。对于测点到复杂曲面的空间距离,可利用基于STL模型的测点与三角面片的隶属关系计算获得[3];针对问题二,本文采用改进的序列二次规划算法实现测量点与理论曲面的最佳匹配,求得最优坐标变换矩阵。
2.1 算法描述
对于约束非线性规划问题,通常的数学描述如下:
[min f(x)s. t. ci(x)=0, i∈E ci(x)≤0, i∈I] (9)
式中,[fx]和[cix]为定义在[Rn]上的函数。[fx]为优化的目标函数;[cix]为约束函数;[E=1, 2, …,n];[I=n+1, …,m]。序列二次规划(Sequence Quadratic Program,SQP)算法主要在某问题的近似解处,将初始的非线性规划问题拆分为一系列二次规划的子问题,通过对子问题的求解,获得下降方向,下降步长由罚函数决定,循环迭代逼近最优解[4]。由于SQP算法具有良好的理论基础及较强的边界搜索能力,因此,在解决非线性约束优化问题中得到了广泛应用。对于求解一般约束非线性规划问题,序列二次规划的子问题在第[k]次迭代求解时,其计算公式可表示为:
[mind dTWkd+∇f(xk)Tds. t. ci(xk)+∇ci(xk)d=0 ci(xk)+∇ci(xk)d≤0] (10)
式中,[Wk]为拉格朗日近似海瑟矩阵;[d]为搜索方向;[∇f(xk)]为目标函数在[xk]处的梯度向量;[cixk]表示不等式约束在[xk]点的值;[∇ci(xk)]为不等式约束在[xk]处的雅克比矩阵。序列二次规划算法的具体算法流程参见周敏的研究[5]。
在利用SQP算法求解二次规划子问题的过程中,罚函数的选择和调整相对比较困难,选用过大或者过小的罚函数都会对计算结果造成一定的影响,而且求解多个子问题的计算量相对较大,在一定程度上影響算法的效率。
2002年,邓迪大学Fletcher和Leyffer[6]提出过滤算法。与传统算法相比,过滤算法在二次规划子问题的求解中,无需使用罚函数。该算法的重点主要是由滤子来代替传统的罚函数,允许一个迭代步被滤子接受当且仅当目标函数值充分下降或违反约束度函数充分下降,其核心是判断目标函数值或约束违反度函数值是否能在试探点非单调下降,如果该点非单调下降,那么就将该试探点作为下一个迭代点进行计算。滤子算法的最大优势在于降低罚因子在调整上的困难,借鉴了多目标优化的算法结构,将约束优化问题转换为双目标优化问题,即可以使目标函数和约束违反度在共同减小时不同步。该算法实质上是一种非单调的方法,有利于提升算法的计算效率,并能得到非线性优化问题的最优解[7-9]。因此,本文采用过滤算法与序列二次规划相结合的方式求解实测点与理论曲面的最优匹配参数。
2.2 误差计算流程
针对无基准复杂曲面轮廓度误差评定问题,根据刘美玲[10]提出的对滤子SQP算法的构造及算法流程的描述,通过对复杂曲面的轮廓度误差评定模型的建立,将(Δx,Δy,Δz,α,β,γ)作为算法优化参数,结合基于STL模型的点到曲面的距离函数,计算获得曲面轮廓度误差值。复杂曲面轮廓度误差值的计算流程如图2所示。
3 仿真实验及分析
本文以如图3所示的复杂曲面为研究对象,借助MATLAB的强大数学计算功能[11],利用数值模拟仿真的方式验证所提出算法的有效性。
在曲面上提取80个测点,添加服从正态分布的随机误差[N](0,0.05),考虑到实际检测过程中测量坐标系与理论坐标并不重合,添加系统误差syserror (0.4,0.4,0.4,-0.2,
-0.2, 0.3)得到模拟实测点集。通过数值模拟仿真计算后,本方法求得曲面轮廓度误差为0.261 5mm。为了进一步验证本文提出方法的准确性,将本方法的计算结果与王东霞等学者[12]所提方法的计算结果进行对比。利用王东霞等学者[12]所提出的方法计算获得轮廓度误差为0.310 4mm。通过数值结果的对比可以看出,本文所提出的算法在复杂曲面轮廓度误差评定中具有更好的评定精度。
4 结论
本文通过对复杂曲面轮廓度误差评定模型的分析,采用过滤算法与序列二次规划相结合的方式优化模型匹配参数,克服了序列二次规划算法本身的局限性,提高了求解优化匹配参数的效率。实验结果表明,该方法能有效实现复杂曲面轮廓度误差的精确评定,在实现复杂曲面的高精加工方面具有一定的参考价值。
参考文献:
[1]张美.自由曲面测量采样策略及轮廓度误差评定算法研究[D].天津:天津大学,2013.
[2] Geometrical product specifications (GPS) — geometrical tolerancing — tolerances of form, location and run-out: ISO 1101—2017[7].
[3]马文魁.复杂曲面加工误差补偿方法与关键技术研究[D].天津:天津大学,2016.
[4]王佳凯,桂胜华.约束非线性优化的二阶段滤子SQP算法[J].上海第二工业大学学报,2006(4):279-286.
[5]周敏.约束非线性优化的信赖域滤子SQP算法[D].洛阳:河南科技大学,2014.
[6] Fletcher R, Leyffer S. Nonlinear programming without a penalty function[J]. Mathematical Programming Ser A,2002(2):239-269.
[7]张家昕.不等式约束优化的一个滤子SQP算法[J].安徽科技学院学报,2015(5):62-65.
[8]刘泽显.一种修正的线搜索Filter-SQP算法[J].系统科学与数学,2014(1):53-63.
[9]非线性互补约束均衡问题的一个滤子SQP算法[J].应用数学学报,2012(1):49-58.
[10]刘美玲.带等式约束二次规划子问题的滤子SQP算法[J].数学的实践与认识,2015(14):272-279.
[11]王鹏飞,王建锋,王晋鹏,等.基于机床运动学模型的加工面形误差影响因素[J].制造技术与机床,2019(2):130-135.
[12]王东霞,温秀兰,赵艺兵.基于CAD模型引导测量的自由曲面定位及轮廓度误差评定[J].光学精密工程,2012(12):2720-2727.
