数学课堂教学中的诗意

付卫国

摘 要：通过创设一次情境，使学生在生动的教学氛围中掌握了“三角形内角和为1800”的证明。

关键词：数学教学;情境

《义务教育数学课程标准》指出：“数学教学要紧密联系学生的生活环境，从学生的经验和已有知识出发，创设有助于学生自主学习、合作交流的情境”[1]。合理有趣的教学情境是实现初中数学有效教学的基础，教师在数学课堂教学中要做到目的明确，要着眼于学生的兴趣点和认知水平，创设合理有趣的课堂教学情境，从而让学生在生动的教学氛围中学到更多的数学知识，感受到数学学习的乐趣。本人在《三角形的内角》一课的教学中[2]，基于这一理念，进行了一次有趣的情境创设尝试。

在小学数学中，学生用剪刀将三角形三个内角剪下拼在一起，发现了三个内角和为1800，而在初中的教学中则需运用所学知识，通过推理而得出结论。那么运用什么知识进行推理呢？本人从“剪刀”这一工具出发，创设了一个有趣的情境。

情境一：赏剪刀

要证明三角形三内角和为1800，关键是如何将三个内角移动拼在一起形成一个平角，这就需要找到一把“剪刀”。此时正是柳树叶盛之期，本人便从贺知章的《咏柳》诗句“碧玉妆成一树高，万条垂下绿丝绦。不知细叶谁裁出，二月春风似剪刀”入手，运用幼灯片配上图片与音乐，师生一起“赏剪刀”。

情境二：用剪刀

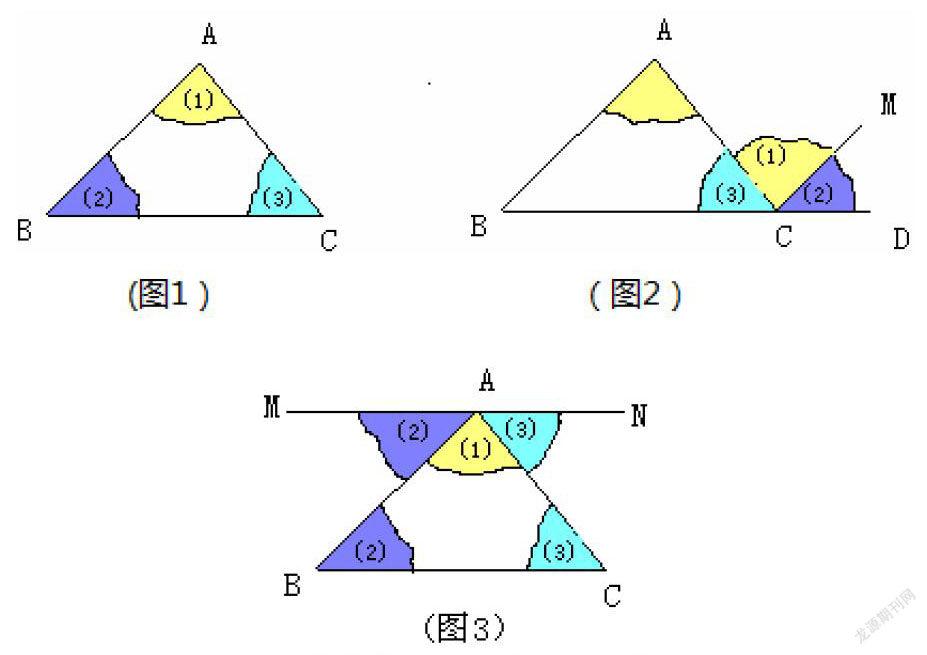
回顾在小学四年级时用剪刀验证三角形内角和等于1800的过程。

观察拼图过程，引出课题，点出本节课学习目标。

情境三：找剪刀

观察上面拼图2过程，联想到平行线，回顾平行线性质，从而找到数学中的思维“剪刀”，尝试证明。

已知△ABC，求证：∠A+∠B+∠C=1800。

证明：延长BC到D，过点C作CM∥AB，

则∠A=∠ACM，∠B=∠DCM，

又∠ACB+∠ACM+∠DCM=1800

∴∠A+∠B+∠ACB=1800。

情境四：试剪刀

由图3你又能想到什么证明方法？请说说证明过程。

已知△ABC，求证：∠A+∠B+∠C=1800。

证明：过点A作MN∥BC，则∠B=∠MAB，∠C=∠NAC，

又∠BAC+∠MAB+∠NAC=1800

∴∠BAC+∠B+∠C=1800。

情境五：得剪刀

小结找剪刀的过程与思考方法，发现平行线性质可看成一把“剪刀”，也可以将角“剪下来”，移到其他地方去。

情境六：玩剪刀

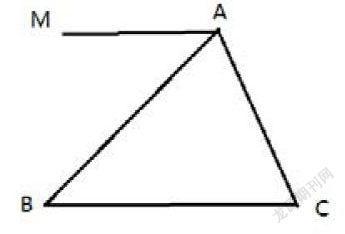
请你用平行线的性质3这把剪刀，证明三角形的三个内角和等于1800。

已知△ABC，求证：∠A+∠B+∠C=1800。

证明：过点A作MA∥BC，则∠B=∠MAB，∠MAC+∠C=1800

∴∠BAC+∠B+∠C=1800。

情境七：耍剪刀

作業布置：

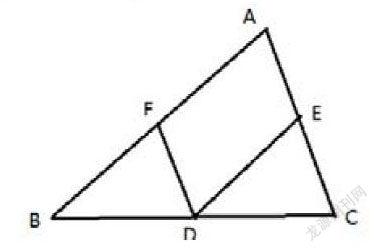
如图，在△ABC中，点D处如此作平行线，

请你证明三角形三内角和为1800。

这堂课内容是八年级上册内容，而我是在七年级学完了整个平行线知识后，给七年级同学上的这一堂课，旨在根据教学经验对平行线的性质应用作一个全面的归纳。课后，学生反应强烈，认为有了这个归纳，让他们对平行线的性质掌握有了质的飞跃。参加听课的老师在评课中说，这是一堂赋有诗意的数学课。

参考文献

[1]中华人民共和国教育部.义务教育数学课程标准（2011 版）[M].北京：人民教育出版社，2011.

[2]义务教育教科书八年级数学教材 [M].北京：人民教育出版社，2012.