乔伊斯分地问题研究

潘璐 雷桂林 李金霞 张新国

内容提要：对于用一条直线平分刀形土地的问题，分别找到了一纵解、一横解、一斜解，进而找到了三个有心集合解。分析了剩余区域，恰好是三个无心集合解。提出了其它的找解的方法都可得到与六个解集相同的结论。由此得出了两个引理：过平面上图形外给定点，可以引一条直线将该平面上的单连通封闭图形面积平分，且只能引一条直线;给定平面上一直线方向，可以做一条该直线平行线，把图形面积平分，并且只能引一条。得出了后面的两个推论。最后得到结论：用一条直线平分刀形土地的六个集合解是平分直线的完备集。

关键词：数学游戏 小学数学教学 面积平分线 集合方法

中图分类号：O123（注：O是英文字母）                         文献标识码：A

1. 引言

参考文献[1]用一条直线将一块由五个边长为1的正方形拼成的“刀形”土地平均分成两块。我们先找到了许多特殊解，继而找到了某类集合解，集合解又分为两类，有心集与无心集。另外，还找到了另外一种求解集的方法。

后来发现有些解集是重合的，最后给出了一种完备的表述方法，其他表述被包含其中。

2. 有心集合解

2.1. 有心集合Ⅰ区解

2.1.1. 纵向平分线

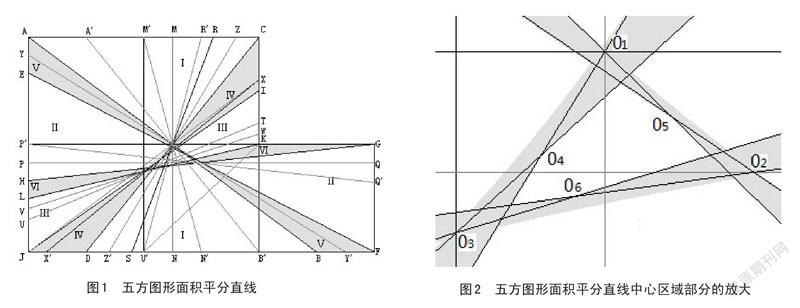
一条纵向解线，在图1中，竖直线MN距左边1.25，它将五方图形左右平分，使左右两侧的面积分别为2.5，MN中点为O1。

2.1.2 有心集合解Ⅰ区解：

在图1 AC上任找一点R，连接RO1，并延长交下面为S点。因 ，故两三角形面积相等，从而推出RS也是五方的平分直线，从而得到AC上所有点与O1连线的延长线都是图形平分线。这些平分线都在直线AB、CD（ ， ）所夹的区域内，该区域为有心（O1）集合Ⅰ区。

2.2. 有心集合Ⅱ区解

见图1，先找到一条横向平分线PQ，PQ距下边5/6，其中点为O2。在GH、EF（ ， ）所夹的区域内，任何一条过O2的直线都将平分五方图。（由2.1可证）这是有心（O2）集合Ⅱ区。

2.3. 有心集合Ⅲ区解

同前，先找到一条平分的中间线TU，两点各距下边为 、 ，可知，在IJ、KL圍成的区域内，所有过O3点的直线都将平分五方。

有心集区域的特点是，每个区域的两个对顶三角形的对边是相互平行的。

3. 无心集合区解

3.1. 无心集合区Ⅳ解

即图1中由CD、IJ围成的区域，在CI上任找一点X，连接XJ（虚线），过I作 ，交CD于X'，连接X'X，并设IJ与XX’的交点为 ，则XX’即为在区域Ⅳ内的五方平分线。（证明如下：△XJI与△XJX’是同底等高三角形，（高为平行线 间的距离），故二三角形面积相等，因此 与 的面积相等。前面已知IJ是五分面积平分线，故XX' 也是五方面积平分线。）这些平分线除两条边界线外的所有平分线都不过O4（可以证明），就构成了无心集合Ⅳ的解。

3.2. 无心集合区Ⅴ的解

即图1中由AB、EF围成的区域，也可由解析找在这个区的平分直线方程，介绍如下。以J为坐标原点，JF为x轴，JA为y轴建立坐标系，在V区边界上取点，满足Xy=5的即为一条平分线，在EA上取Y点，测量YJ =1.8，在BF上找Y’点，则JY’=5/1.8=2.78，在BF上找到Y’，YY’即为所找的平分直线，同理可找到所有的平分直线。

3.3. 无心集合区Ⅵ的解

见图1，即图1中直线KL、HG围成的区域。找平分直线的方法可参阅Ⅳ区、Ⅴ区解使用的方法。

无心集区域的特点是，每个区域的两个三角形的对边是相互垂直的。

4. 其他个解与解集

4.1. 其他个解

①纵横各一条平分线，即图1中的MN、PQ。②六个集合的边界线（六条）和中线（六条）。③过每条边的特殊点与中心交叉点的连线，如题1中U’R’、N’M’、B’A’、P’Q’（共四条）。④把五个正方形分成两组中心对称的图形的连心线（图1中，右1与余4;上二与下三;左下1与余4）共得三条）。⑤其他过特殊点的平分线。以上共计二十一条平分线（不计⑤类）。这21条平分线都在六集合内。

4.2. 其他解集

在五方边界上任找两点，如图1中KU’做参考线，可以计算该线和五方图形一侧的面积，如图1中KU’与U’FGK围成的图形的面积为1.5，在KU’的左上侧再做一条线如WV使WV与KU’围成的面积为1，则WV就是要找到平分线。也可以找ZZ’，使ZZ’与KU’围成的面积为1，则ZZ’就是要找到平分线。还可以找到N’M’使M’CKOM’的面积减去△O7U’N’的面积为1，即M’N’为图形的面积平分线。所以这些平分线构成一个解集。这个解集将涵盖前面介绍的六个解集。

同样可以选其他参考线，得到一个解集，而这样的解集有无穷多个。

5. 平面封闭图形直线平分引理和推论

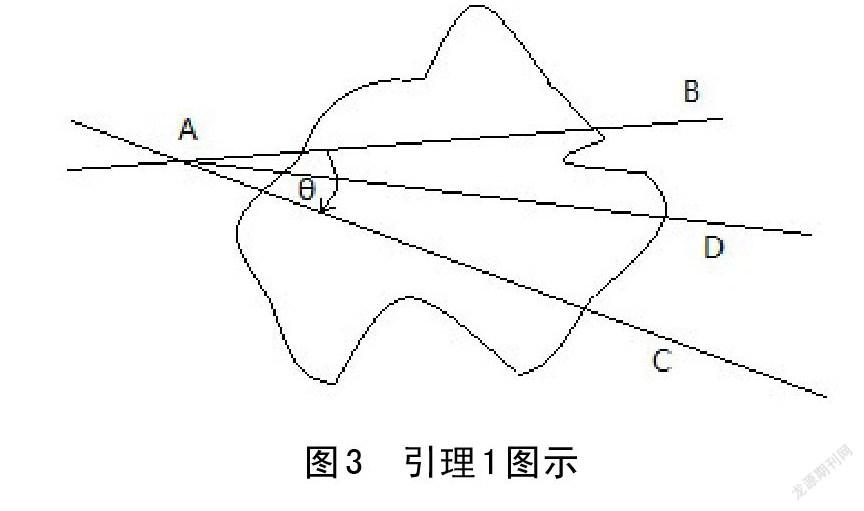
5.1 引理1 过平面上图形外给定点，可以引一条直线将该平面上的单连通封闭图形面积平分，且只能引一条直线。如图2所示，给定点A，过A任作一条直线AB，可以测量图形在AB上面的面积小于AB线面的面积。过A点朝下斜作AC，得到AC下面面积小于上面的面，在它们之间再做一条AD，......因为图形面积变化是连续的，总能找到AD将图形面积平分。过A点的直线随着与AB夹角变大而面积将连续变大，故平分只有一条。

5.2 引理2

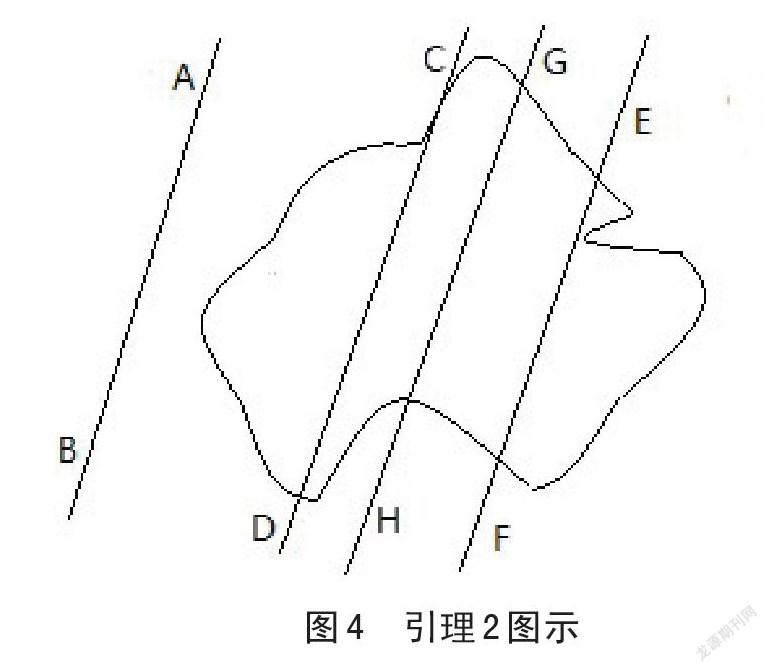
给定平面上一直线方向，可以做一条该直线平行线，把图形面积平分，并且只能引一条。如图3所示，图形外有一条直线AB，先做一条直线CD，使CD//AB，测量计算发现CD左边的面积小于右边的面积，再做一条直线EF，使EF//AB，测量计算发现EF右边比左边面积大，经过多次总能找一条直线（因为平行线移动左右两边面积将连续变化），使直线GH左右两侧面积相等。

5.3 推论1

过平面上一点封闭图形的平分线必过图形边界;过平面各点的封闭图形平行线走遍封闭图形边界上各点，即过图形边界上各点的平分直线是图形平分直线的完备集。

5.4 推论2

平行于平面上已知直线对封闭图形的平分直线必过图形边界;平行于平面上各方向的封闭图形的平分线走遍封闭图形的边界上各点，也即图形边界上各点的平分直线是图形平分直线的完备集。

5.5 结论

平分五方问题的六集合解，是平分直线的完备集。

参考文献

[1] 闻钟.优秀小学生必做的1000个思维游戏[M].南京大学出版社.2015..

[2] 常国庆.研究性学习“三步曲”——以“平面多边形面积平分线性质的探索”为例.教育研究与评论（中学教育教学）. 2015，（7）：82-90.

[3] 张小川，翟双. 一类面积问题的推广. 中国数学教育. 2018，（7-8）：101-103.