基于磁致伸缩逆效应的纹理触觉传感器研究
2019-09-10万丽丽王博文索峰黄文美翁玲
万丽丽 王博文 索峰 黄文美 翁玲









摘要 纹理是物体表面微观结构分布特征的体现,为了提取不同物体表面微观结构特性,提出一种基于Galfenol材料的新型磁致伸缩触觉感知系统。基于磁致伸缩逆效应、悬臂梁挠度理论等建立纹理触觉传感器输出电压与纹理表面微观结构的关系。实验选取5种织物样本测试,测试的输出电压明显不同,然后利用MATLAB软件提取输出电压中与纹理有关的峰值平均电压和功率谱密度,表明在粗糙度大于6.0的范围内,传感器可以识别物体的粗糙度;在细密度大于6时,细密度的识别具有较高的灵敏度。最后通过测试触觉传感器的线性度为0.019%,灵敏度为97.31 mV/mm,重复性小于0.33%,验证纹理触觉传感器的稳定性,满足设计要求。
关 键 词 纹理触觉传感器;磁致伸缩逆效应;Galfenol;挠度;功率谱密度
中图分类号 TP212.1 文献标志码 A
Research on texture tactile sensor based on inverse magnetostrictive effect
WAN Lili1,2,3, WANG Bowen1,2, SUO Feng1,2, HUANG Wenmei1,2, WENG Ling1,2
(1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment, Hebei University of Technology, Tianjin 300130, China; 2. Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province, Hebei University of Technology, Tianjin 300130, China; 3. School of Logistics Engineering, Tianjin Transportation Technical College, Tianjin 300110, China)
Abstract Texture is the embodiment of the distribution of microstructures on the surface of an object. In order to extract the surface microstructure characteristics of different objects, we propose a new magnetostrictive tactile sensing system based on Galfenol. Based on the inverse magnetostrictive effect and the deflection theory of beam, the relationship between the microstructure of the textured surface and the output voltage is established. Five fabric samples were tested in the experiment, and the output voltages of texture tactile sensor were significantly different. Then MATLAB software was used to extract the peak average voltage and power spectral density related to texture from the output voltage signals. The experimental results show that the tactile sensor can identify the roughness of the object when the roughness is greater than 6.0. In the range of fineness greater than 6, and the tactile sensor has higher sensitivity. Finally, by testing the static parameters of linearity (0.019%), sensitivity (97.31 mV/mm), and repeatability (less than 0.33%), the texture tactile sensor is verified to be stable and meet the design requirements.
Key words texture tactile sensor; inverse magnetostrictive effect; Galfenol; deflection; power spectral density
近年來,触觉传感器的发展一直是机器人领域的热门话题。与动态环境交互的机器人系统,在利用高级视觉技术识别对象属性时,会存在被遮挡、光线不足和精度低等影响因素,所以完成机器人与动态环境交互一直是一项至关重要但很困难的任务。而触觉感知能捕获多个接触点,接触区域信息丰富还能获得直接的反馈[1-4]。触觉装置的性能主要取决于触觉传感器。触觉传感器基于敏感元件换能原理进行分类,一般可以分为:压电式传感器、电容式传感器、光电式传感器、超声式传感器、电磁式传感器、压阻式传感器和有机可弯曲、拉伸传感器等[5-7]。这些传感器可以提供一些触觉或触摸信息,这些信息可以表征物体的重量、刚度、弹性和摩擦力等。实际上物理对象特征描述可以分为3大类,分别描述的是物体的形状信息、内部属性和材料属性[8-9]。其中物体的材料属性又可以通过刚度、导热性和纹理特征来表征。人手之所以能够识别物体的粗糙度纹理特征,主要是由人手皮肤中丰富的机械刺激感知小体来决定的。在服务机器人系统中,表面纹理特征被认为是用于评估和识别物体的重要信息。目前,由于非视觉纹理传感器的设计难度较大,对精细几何纹理的样本有效测量仍然是一项具有挑战性的任务。磁致伸缩材料具有饱和磁场小,延展性好,抗拉强度高的特点,可承受各种机械载荷,如压力、张力和冲力等。而且磁致伸缩逆效应表明,磁致伸缩材料的磁导率可以通过外部冲击而改变。同时触觉传感器输出特性与物体纹理的关系一直不清楚,并且触觉传感器的输出电压的理论模型尚未建立。因此本论文首先提出基于Galfenol材料设计,制作了一种新型的用于纹理探测的触觉传感器系统。其次根据磁致伸缩逆效应、霍尔效应、和欧拉-伯努利梁结构动力学理论等,建立了纹理触觉传感器的输出电压模型。通过分析测试数据提取峰值电压、功率谱密度表征物体纹理属性。
1 纹理触觉传感系统
本纹理触觉传感器主要由探针触头、Galfenol片、励磁线圈和两个霍尔元件构成。本研究中的Galfenol材料选用的是取向<100>,织构化多晶的Fe83Ga17合金薄板。Galfenol片的两端分别安装一个霍尔元件。该霍尔元件分别完成信号采集和样本破坏性检测。励磁线圈提供了沿着梁的长度方向的偏置磁场。探针触头直接接触移动被测物体从而引起Galfenol片自由端上下振动。整个触觉传感器的尺寸是70 mm × 20 mm × 20 mm,重量为20 g,如图1a)所示。该触觉传感系统除了传感器之外,还包括示波器、电源、仿手指的支撑架、带编码器的驱动直流电机、传送带、信号采集单元和计算机等设备。在图1b)中,信号采集单元选用的是12位模数转换器,通过该转换器获取触觉传感器的输出信号。被测物体利用传送带和直流电机实现往复运动。同时直流电机还可以控制传送带的速度、位移和方向。在实验过程中,该纹理触觉传感器是安装在人形机械手支架上,通过支架的支撑和压缩带动触觉传感器触摸移动平台上的纹理物体(样本)。移动平台的运动方向选取的是在x轴方向。为了保证触觉传感器与纹理表面的充分接触,在z轴方向施加正向力。该力是通过类人形机械支架上的电机提供的。当触觉传感器触摸不同纹理的物体时,探针接触到垂直方向的纹理高度,进而引起悬臂梁产生挠度。基于磁致伸缩逆效应,Galfenol片的磁通密度会发生改变,然后利用霍尔元件得到传感器的输出电压。尤其当被测物体纹理触摸过程中发生损坏时,Galfenol片固定端的霍尔元件输出电压更明显,这是由该霍尔元件的安装位置决定的。
为了保证物体纹理测试的准确,该感知系统采用两种方式收集触觉传感器信号,一种是通过示波器直观显示,另一种是由采集卡和模数转换模块将数据上传计算机。
2 纹理触觉传感器输出模型
触觉传感器的输出信号是通过霍尔元件采集的,霍尔元件检测Galfenol悬臂梁内部磁通密度变化,因此得到输出电压与磁通密度关系为
[UH=kHISB], (1)
式中:[UH]是霍尔元件的输出电压;[kH]是霍尔常数;[IS]是通过霍尔单元的控制电流;[B]是Galfenol内部的磁通密度。
该霍尔元件型号为ss491B,它的参考输出电压为2.5 V。为了确保纹理测量的精度,其参考输出电压利用外围电路调整为0 V。即纹理触觉传感器的输出电压直接表示为
[U=UH=kHISB]。 (2)
根据Galfenol的线性本构方程和偏置磁场[H=Nib/l],Galfenol内部的磁通密度B为
[B=dEε+Nib(μ-d2E)/l], (3)
式中:[d]是磁机耦合压磁系数;[E]是楊氏模量;[ε]是悬臂梁长度方向总的应变;[N]是励磁线圈的匝数;[ib]是线圈中的励磁电流;[μ]是磁导率;[l]是Galfenol片的长度。
在图1a)中,梁的纵轴是[x],横轴是[z],因此[xz]平面是梁的中性面。通过假设1)梁为欧拉-伯努利梁;2)Galfenol片沿[x]轴的磁场均匀分布;3)忽略剪切力对梁形变的影响,推导得出挠度函数。该方程组为
[ω=-F6EI(3lx2-x3)] , (4)
[ωfree=-Fl33EI] , (5)
[ω=ωfree2l3(3lx2-x3)], (6)
式中:[x]代表梁上任意点与自由端之间的距离;[F]是施加到梁的自由端的正向力;[I]是截面惯性矩;[ωfree]是在[x=l]处的挠度值,即梁的最大挠度。其中方程(6)是由方程(4)除以方程(5)推导得出的。
利用中性层曲率表示梁的弯曲公式同时忽略剪切力,[x]轴上任意点的梁的应变可表示为
[εx=yρ(x)=yd2ωdx2] , (7)
式中:[y]为梁的表面与中性面的垂直距离,其值等于梁厚度的二分之一;[ρ(x)]代表在[x]轴任意点的挠度曲线的曲率。由式(7)可以看出,应变与挠度有关,挠度反映了悬臂梁的振幅大小,而振幅大小由被测物体的纹理决定。不同纹理面的微观结构复杂程度不同,基于特定的数学模型和几何约束条件可以建立纹理的触觉表达式[10]。
在织物动态粗糙度编码中,触发纹理触觉传感器和速度刺激的相对运动轨迹近似为正弦曲线。当在某时刻,物体刺激的第一个脊与触觉传感器的探针触头接触时,剪切力和正向力都施加在探针触头上。在力的作用下,安装在梁两端的霍尔元件产生了电压脉冲。随着物体刺激的移动,脊一个接一个撞击探针触头,产生了一系列电压脉冲。该脉冲序列揭示了主频率,其与扫描速度和纹理表面间距有关,关系如式(8)所示:
[f=νλ] 。 (8)
对于探针触头,在没有动态效应的情况下,在探索(或测试)期间由接触表面构成触觉传感器Galfenol片的偏转。根据纹理触觉传感器的触头跟踪的偏移表面近似为正弦曲线,其可表示为
[ωfree=Asin(2πft+φ)] , (9)
式中:[A]是正弦曲线的幅值,代表被测物体纹理脊的高度;[φ]是一个反应被测物体接触深度的值。将式(8)代入式(9)得到
[ωfree=Asin(2πνλt+φ)]。 (10)
将式(10)代入式(7),然后积分得到梁长度方向总的应变,其表达式为
[ε=lεxdx=3hA4lsin(2πνλt+φ)] 。 (11)
将式(11)代入式(3)和式(2),得到触觉传感器的输出电压,表达式为
[U=kHIS[4Nib(μ-d2E)+3dEhAsin(2πνλt+φ)]4l] ,
(12)
式中:[A]和[λ]为与被测物体的纹理有关的参数,分别代表纹理表面脊的高度和宽度,随着接触不同的纹理物体,以上2个参数是变化的;[h]是Galfenol片的厚度或者称为高度。另外,纹理触觉传感器的模型还包括一些与霍尔器件和Galfenol材料相关的参量。其中[A],[λ],和[ν],是最重要的影响着触觉传感器输出特性的3个因素。根据式(12),当霍尔元件和梁的材料已确定,通过计算得出传感器触摸不同织物的输出电压,并且该模型对物体纹理识别能提供重要的指导。
3 实验结果与分析
设计的触觉传感器中Fe83Ga17合金片长度为l = 69 mm, 厚度为h = 0.7 mm, 杨氏模量为E = 70 GPa, 磁机耦合压磁系数是d=34 T/GPa[11]。其它参数,励磁线圈匝数N = 200, 励磁电流[ib=0.2 A], 霍尔常数[kH=0.005 63], 霍尔单元控制电流[IS=10 mA]。设定纹理表面和传感器触头的相对速度分别为1 cm/s, 2 cm/s,3 cm/s,4 cm/s,5 cm/s。实验中选取牛仔布、尼龙丝带、薄纱、纱布和粗布作为测试对象,每个测试对象纹理表面是均匀一致的,其测试样本参数如表1。每种样品在相同条件下进行6次实验,通过改变速度,每个样品测出30组实验数据。当测试速度为2 cm/s时,所得5种样本的测试数据,经过滤波得到样本纹理的振动信号如图2所示。从图2可以看出,当纹理触觉传感器接触以2 cm/s的速度移动的织物样本时,传感器的输出电压是随着织物表面脊高和间距而上下移动的。在图2中,a)图和b)图的输出电压分别在50 ~ 60 mV,和55 ~60 mV;然而c)图和d)图的电压分别在恒定电压60 mV和65 mV附近变化;a)~d)图的测试样本主观感知纹理相似,但触觉传感器可以通过输出电压来区分。e)图的输出电压达到170 mV,触觉传感器的输出电压随着纹理的差异越大增加越明显。图2的实验结果与文献[12]相比,通过纹理触觉传感器设计的优化,输出特性明显增强。当织物物体移动速度为2 cm/s时,触觉传感器的输出电压会因纹理不同而输出不同。因此,表面纹理对触觉纹理传感器的输出电压有很大的影响。
粗糙表面比光滑表面更厚重,因此接触表面之间输出振动信号的幅值相对较大,幅值的平均值可以代表粗糙度尺寸[13-15]。为了表征物体粗糙度,利用MATLAB软件对触觉触感器输出信号进行特征提取。图3中的峰值平均值和粗糙度之间的关系是通过MATLAB软件编程处理实验数据得出。图3显示当粗糙度小于6时, 峰值平均电压增加缓慢。当粗糙度在6 ~ 7.5之间时,峰值电压单调增加,而且速度增加很快。以上结果表明,该纹理触觉传感器在测量粗糙度大于6.0的物体时,精度会更高。
触觉纹理传感器输出的时域信号不能完全描述物体的纹理,因此有必要进一步从频域范围进行分析。纹理的细密度可以通过振动信号频谱的谐波最高峰对应的功率谱密度来表征。当被测物体移动速度为2 cm/s时,物体细密度和功率谱密度的关系如图4所以。从图4中得出,功率谱密度随着细密度的增加而增加,尤其当细密度大于6时,功率谱密度增加更明显。结果表明功率谱密度也能表征物体纹理特性。
4 纹理触觉传感器静态特性
4.1 线性度
线性度是触觉传感器的一个重要指标,是指输入输出曲线与理论拟合直线的最大偏差与传感器满量程输出值的比值,可以表示为
[γL=±ΔLmaxYFS×]100% , (13)
式中:[γL] 为线性度;[ΔLmax]为实际测量曲线与拟合直线间存在的最大非线性绝对误差;[YFS]是满量程输出值。
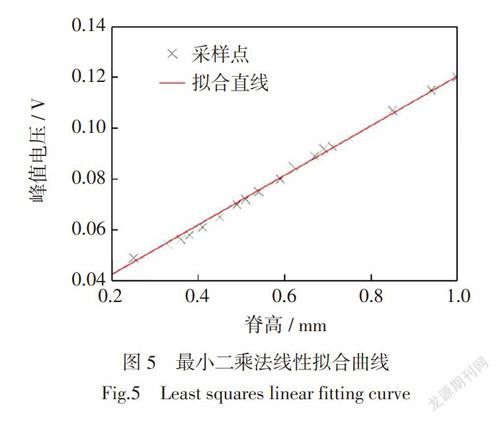
设置采样点20个,满量程1 mm,[YFS]为120 mV,利用公式(12)计算得到采样点数据,然后应用最小二乘法线性拟合得到输入输出曲线,如图5所示。图5中测得传感器的最大非线性绝对误差 ,最小二乘法拟合直线斜率0.097 31,拟合直线方程为[U=0.097 31×A+0.023 07],因此在0.2 ~ 1.0 mm的量程范围内传感器线性度[γL=0.019%]。
4.2 灵敏度
灵敏度是传感器在稳态下输出量变化对输入量变化的比值,从图5中拟合直线推导得出,触觉传感器的灵敏度为97.31 mV/mm。
4.3 重复性
重复性表示传感器在输入量按同一方向作全量程多次测试时所得输入-输出特性曲线一致的程度[16-17]。重复性指标一般采用输出最大不重复误差[ΔRmax]与 满量程输出[YFS]的百分比表示,即
[γR=±ΔRmaxYFS×100%] 。 (14)
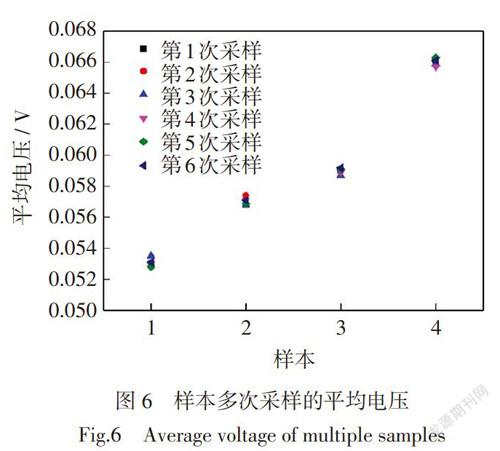
实验中选取4种不同织物(表1)测量触觉传感器的重复性,每个样本重复测量6次,得到6组测量数据,如图6所示。6次测试结果取平均值得到四种织物输出的平均电压分别为53.05 mV,57.05 mV,59 mV,66.03 mV。按照公式(14)计算得到4种织物的重复性分别为0.35%,0.35%,0.33%,0.32%。多次按相同輸入条件测试的输出数值越一致,其重复性越好,误差越小。从测试4种织物结果也能得到,该触觉传感器对粗糙度和细密度大于6的织物测量误差小,重复性小于0.33%。
5 结论
本文设计并制作了一种新型触觉传感系统,该系统用于通过模仿人体活动纹理感知过程来测量织物表面纹理。基于磁致伸缩逆效应、挠度理论和本构方程,建立物体纹理表面微观结构与输出电压的模型。采用纹理触觉传感器对五种不同织物样本进行检测,经过滤波得到振动的电压信号,然后利用MATLAB软件实现峰值平均电压和功率谱密度特征提取。结果表明粗糙度大于6.0的范围内,传感器对物体粗糙度识别灵敏度较高;在细密度大于6的范围内,提取的功率谱密度的方法对细密度的识别灵敏度高。最后触觉传感器性能分析也表明,该传感器的稳定性较好,表明通过该纹理触觉感知系统提取的特征值能够实现纹理检测,也为系统后续纹理自动识别提供指导。
参考文献:
[1] KUANG L S,LOU Y J,SONG S. Design and fabrication of a novel force sensor for robot grippers[J]. IEEE Sensors Journal,2017,18(4):1410-1418.
[2] MOHSEN K,CHENG G. Robust tactile descriptors for discriminating objects from textural properties via artificial robotic skin[J]. IEEE transactions on robotics,2018,34(4):985-1003.
[3] CAO J G,ZHOU J H,LIAO C X. Research progress and development trend of electronic skin touch sensor[J]. Journal of Harbin Institute of Technology,2017,49:1-13.
[4] MOHSEN K,CHENG G. Robust tactile descriptors for discriminating objects from textural properties via artificial robotic skin[J]. IEEE Transaction on Robotics,2018,34(4):985-1003.
[5] SPANU A,PINNA L,VIOLA F,et al. A high-sensitivity tactile sensor based on piezoelectric polymer PVDF coupled to an ultra-low voltage organic transistor[J]. Organic Electronics,2016,36:57-60.
[6] 王博文,王启龙,韩建晖,等. 磁致伸缩压力传感器设计及其输出特性[J]. 光学 精密工程,2017,25(4):396-401.
[7] ZHENG W,WANG B,LIU H,et al. Structural design and output characteristic analysis of magnetostrictive tactile sensor for robotic applications[J]. AIP Advances,2018,8(5):056622.
[8] ASANO S,OKAMOTO S,YAMADA Y. Vibrotactile stimulation to increase and decrease texture roughness[J]. IEEE Transactions on Human-machine Systems,2015,45(3):393-398.
[9] NAKAMOTO H,NISHIKUBO D,KOBAYASHI F,et al. Development of food texture sensor using two magnetic sensing elements[C]//IEEE Symposium Series on Computational Intelligence (SSCI). Cape Town,South Africa,2015. DOI 10. 1109/SSCI. 2015. 27.
[10] CHEN S,GE S,TANG W,et al. Tactile perception of fabrics with an artificial finger compared to human sensing[J]. Textile research journal,2015,85(20):2177-2187.
[11] WAN L,WANG B,WANG Q,et al. The output characteristic of cantilever-like tactile sensor based on the inverse magnetostrictive effect[J]. AIP Advances,2017,7(5):056805.
[12] 王博文,王晓东,李云开,等. 用于纹理探测的磁致伸缩触觉传感器[J]. 光学 精密工程,2018,26(12):2991-2997.
[13] OTADUY M A,LIN M C. A perceptually-inspired force model for haptic texture rendering[C]// Symposium on Applied Perception in Graphics and Visualization. ACM,2004:123-126.
[14] 俞平. 智能假肢指尖動态触觉传感阵列设计及纹理识别方法研究[D]. 杭州:浙江大学,2017:47-57.
[15] JAMALI N,SAMMUT C. Majority voting:Material classification by tactile sensing using surface texture[J]. IEEE Transactions on Robotics,2011,27(3):508-521.
[16] 胡向东. 传感器与检测技术[M]. 第2版. 北京:机械工业出版社,2013:15-18.
[17] 张露予. 螺旋磁场与应力作用下磁致伸缩位移传感器的输出特性研究[D]. 天津:河北工业大学,2016:89-94.
[责任编辑 田 丰]
