配合城市轨道交通的接运公交车区域布设

孙文霞　胡莉芳

摘要 为了充分发挥轨道交通在城市交通中的骨干作用以及接运公交的集散作用，提出了配合城市轨道交通的接运公交车区域布设模型。分析城市轨道交通与接运公交之间的关系，提出边际出行距离的概念，即选择常规公交直达以及选择常规公交—轨道交通换乘所消耗的广义成本，其中特别考虑了服务水平对乘客选择的影响。并对居民收入水平、轨道交通的票价设置以及乘常规公交距离与出行总距离的比值大小对于边际出行距离的影响进行了敏感性分析。进而考虑各站点的OD分布，建立以全部乘客总出行时间最小值为目标，以边际出行距离为约束条件的区域布设模型并设计算法求解。最后通过对北京市5号线城市轨道交通与常规公共汽车之间衔接的数值实例进行分析，显示了该模型符合实际情况，易于应用。

关 键 词 接运公交;边际出行距离;区域布设

中图分类号 U491.17     文献标志码 A

With the layout of regional city rail transit feeder bus

SUN Wenxia， HU Lifang

（School of Civil Engineering and Transportation， Hebei University of Technology， Tianjin300401，China）

Abstract In order to give full play to the backbone role of rail transit in urban transportation and the role of collection and distribution of pick-up buses， a regional layout model of pick-up buses matching with urban rail transit is proposed. This paper analyzes the relationship between urban rail transit and pick-up bus， and puts forward the concept of marginal travel distance， that is， the generalized cost of choosing direct bus and transfer between normal bus and rail transit， especially considering the impact of service level on passenger selection. In addition， sensitivity analysis is made on the influence of residents' income level， ticket price setting of rail transit and the ratio of the distance between conventional public transport and the total travel distance on the marginal travel distance. Then， considering the OD distribution of each station， a regional layout model with the minimum total travel time of all passengers as the goal and the marginal travel distance as the constraint condition is established and the algorithm is designed to solve it. Finally， through the analysis of the numerical example of the connection between the urban rail transit and the conventional bus of Beijing line 5， it shows that the model is in line with the actual situation and easy to apply.

Key words feeder bus; marginal travel distance ;regional layout

0 引言

城市的迅猛發展带来了诸多的城市交通问题，特别是交通堵塞，严重影响了人们的生活水平。为了缓解交通拥堵，公共交通便是其中的一个有效方法，其中以城市轨道交通以及公共汽车为主。通过业内人士统计，截止2017年上半年，全国的城轨运营总里程已经长达4 400 km，预计到2020年，城轨交通运营的运营总里程将会有6 000～7 000 km之长。随着城市轨道交通建设的日益完善，常规公交网络与轨道交通的整合也显得愈发刻不容缓。

近年来，对于公共交通线网的优化一直是研究热点。Pattnaik等[1]对公交线网设计中，将乘客出行的费用最小化、运营费用最小化作为目标，构建了模型，并应用遗传算法对其优化计算。Kuan等[2]为了解决总线网络优化的N-P问题，介绍了一种启发式遗传算法来求解。许旺土等[3]考虑轨道交通接运公交发车间隔及票价的乘客需求弹性，对接运公交系统的成本及收入进行分析，以最大系统总收益值为目标，同时考虑轨道客运量份额为主要约束条件设计了非线性规划模型，通过Matlab软件求解。郭本峰等[4]在分析土地性质、出行需求以及公交运营成本等主要影响因素的基础上，研究了配合轨道交通的接运公交的最优长度以及线路布设问题。马宇红等[5]针对M-M乘客的需求模式，对于接运公共交通的网络进行了优化设计，应用逆向径向扫描算法生成基本的线路，然后通过线路优化算法对基本线路优化，并结合实例证实了算法的可行性。Yu等[6]在接驳网络领域提出了一种禁忌搜索算法，既可以保证准确性，又可以提高计算效率。刘华胜等[7]考虑了交通堵塞，利用复杂网络知识提出了有效路径，建立双目标模型布设接运公交的线路。

目前，国内在常规公交的线网优化上取得了一些成绩，然而我国的轨道交通网络并不很完善[8] 。随着轨道交通的建成，关于接运公交连接区域和线路布局的研究比较少，只有薛兴建提出了轨道交通公交车布局区域模型，然而一些参数的选择存在问题，且很少考虑交通OD分布的影响，基于此，这项研究中，考虑了OD分布与舒适度对乘客选择的影响，并以北京五号线为实例进行分析，显示了对以往模型的修正，为接运公交的布设区域提供了比较实用的判断方法。

1 边际出行距离

1.1 轨道交通与常规公交的关系

轨道交通相比常规公交服务质量较高，不存在交通堵塞问题，且单位时间内有相当高的客运量，路权高，且比较安全，然而需要比较高的投资，机动性没有常规公交好。接运公交属于常规公交，主要功能是集散乘客，从而配合轨道交通服务。其关系示意图见参考文献[9]。

常规公交与轨道交通的关系有：竞争客流、集散客流、总体上存在轨道交通竞争客流，却也有一定的为轨道交通集散客流的作用、无明显关系主要为常规公交系统提供服务。在实际中，为了发挥轨道交通的骨干作用与接运公交的集散作用，通常可以采取如下措施：

1）如果公交线与轨道交通同路的路线比较长，则需要将此条线路改道;此外，倘若该公交线上的客流比较多，则可酌情对其不进行改道，以此分担部分客流量，体现其对于轨道交通的集散作用，同时需要注意限制公交与轨道交通的重叠线路的长度，通常不宜应该超出3个轨道站区间的长度。

2）为了方便乘客换乘，可以增加接运公交线，使之与轨道线垂直或者交叉。

3）公交线首末站要向就近的轨道线终点靠拢，或局部改道使其途经轨道站，或延伸首末站至轨道站。

1.2 改善边际出行距离

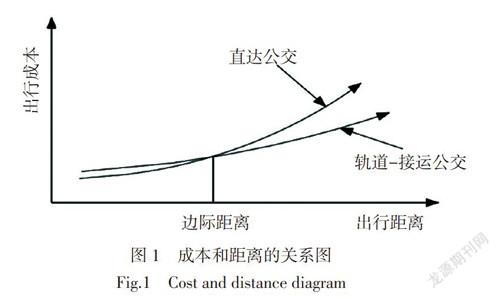
人们在出行的时候可以选择不同的交通方式来达到目的地。乘客往往倾向于较高的出行舒适度与较短的时间以及较低的出行成本，然而这3种倾向存在博弈现象，基于此，可以引出边际出行距离，它指的是：乘客通过选择不同的交通方式到达同一目的地，消耗相同的出行成本的出行距离。影响出行成本的因素有：单位时间价值，乘客等待与转移时间，常规公共交通的旅行距离和总行驶距离的比例，票价与乘客舒适度等。

本文主要计算乘客选择轨道-接运公交换乘与选择常规公共交通直达目的地2种方式的消耗相同的出行成本，得出边际出行距离。

1.2.1 参数定义

D代表出行总距离;E代表单位时间价值，单位是元/ min;α代表步行、等待时间价值系数;β代表乘车时间价值系数;[Tw]代表乘客集散时间（乘客从出发点到站点乘上车时间与从站点下车到目的地时间之和）;[v1]代表常规公交的平均速度;x代表公交车票价;s代表常规公交的起跑距离;[Td]代表乘客换乘等待时间;[Tv]代表乘客换乘步行时间;[λ]代表出行中选择常规公共交通的行驶距离与总行驶距离的比例;[v2]代表轨道交通的平均速度;y代表轨道交通票价;[C2]代表接驳公交车转乘轨道交通的乘客舒适水平;[δ]代表常规公交单位公里票价;[C1]代表常规公共交通的乘客舒适水平。

1.2.2 模型建立

乘客选择常规公共交通直达产生的出行成本[10]

[FT1=TwEα+DEβv1+x+（D-s）δ+C1]， （1）

式中：[TwEα]代表乘客集散时间成本;[DEβv1]代表公交乘车时间成本;[x+（D-s）δ]代表公交乘车货币成本。

乘客选择接运公交—轨道交通一次换乘产生的出行成本

[FT2=（Tw+Tv+Td）Eα+λDv1+（1-λ）Dv2Eβ+x+（λD-s）δ+y+C1]， （2）

式中：[（Tw+Tv+Td）Eα]代表乘客集散时间成本、换乘步行时间成本和换乘等待时间成本之和;[λDv1+（1-λ）Dv2Eβ]代表公交乘车时间成本和地铁乘车时间成本之和;[x+（λD-s）δ]代表公交乘车货币成本;[y]代表轨道交通乘车货币成本;量化舒适度与时间成本的转化关系[C1-C2=1]元。

常规公共交通直达和轨道-接运公交一次换乘的出行的边际出行距离模型为

选择轨道 - 接运公交换乘的出行成本 = 选择常规公共交通直达的出行成本，

即 [FT1=FT2]， （3）

同时将式（1）和式（2）代入式（3），经简化，結果是

[D=C1-C2-（Tv+Td）Eα-y（1-λ）Eβ1v2-1v1-δ]。 （4）

1.3 敏感性分析

研究因素变化后对于边际出行距离的影响。

1.3.1 居民人均收入的敏感性

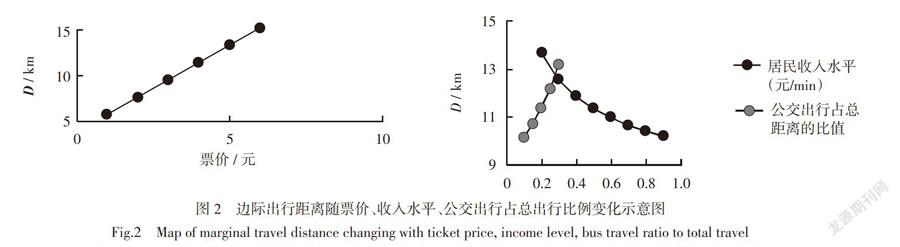
参考北京收入相关数据，2017年北京职工月平均工资为6 909元，月人均可支配收入为4 769元。故而取E = 0.5。根据不同的收入水平对边际出行距离进行分析，令轨道交通票价与常规公共交通的行驶距离和总行驶距离的比一定，即λ = 0.2，y = 4可以得出下图2。

根据图2可知，边际出行距离随着收入的增长在慢慢减少，两者呈现负相关的趋势。随着人们收入水平的提高，边际出行距离的减少意味着：相同的出行距离下，人们往往更容易选择换乘比较舒适快捷的轨道交通，即选择轨道交通与常规公交接驳的方式出行。

1.3.2 轨道交通票价的敏感性

根据不同轨道交通票价对边际出行距离进行分析，令收入水平与常规公共交通的行驶距离和总行驶距离的比一定，即λ = 0.2，E = 0.5 可以得出下图2。

根据图2可知，边际出行距离随着票价的增大而增大，减少而减少，两者呈现正相关的趋势。随着轨道交通票价逐渐提高，人们往往更倾向于选择常规公交直达，进而导致边际出行距离的扩大，不利于发挥轨道交通的骨干作用。因此，轨道交通的票价不宜定得过高。

1.3.3 常规公共交通的出行距离和总行驶距离之比（λ）的敏感性

根据常规公共交通的行驶距离和总行驶距离的比对边际出行距离进行分析，令收入水平与轨道交通票价一定，即E = 0.5，y = 4 可以得出下图2。

根据图2可知，边际出行距离随着λ的增长而增长，减小而减小，两者呈现正相关的趋势。表明了随着人们乘坐公交车的运行距离越短，越容易换乘轨道交通，即接运公交的长度设置越小对于刺激人们换乘的作用越明显。

在边际出行距离之内出行，人们可以选择公交直达满足自己的出行需求，其出行成本较低，在边际出行距离之外出行，通常選择常规公交车—轨道交通换乘更适合，因为此时换乘的交通成本比直达公交要低。对居民收入水平、轨道交通的票价设置以及乘常规公交距离与出行总距离的比值大小对于边际出行距离的影响进行了敏感性分析。发现边际出行距离在通常情况下是9～14 km。

2 接运公交布设区域模型构建

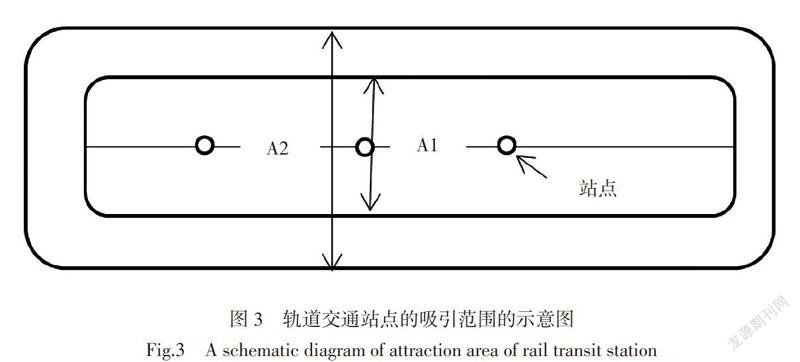
一般地，轨道交通的客流可以分为一次吸引客流以及二次吸引客流。乘客或通过步行，或通过其他的非步行交通方式到达轨道交通站点进行换乘，前者称为一次吸引客流，后者称为二次吸引客流，在我国，乘客主要通过公交换乘。

如图3，A1、A2分别代表城市轨道交通的一次吸引范围、二次吸引范围。其中A1小于等于1.34 km，A2在5.2～8.2 km之间[11]。

在考虑交通需求的基础上，进行接运公交布设更可以符合实际情况，公交客流OD矩阵是城市公共交通线网布设和优化的基本依据，因为各个公交站点的交通需求是不一样的，而不同的交通需求也影响到乘客消耗的总时间。

基本思路：假设从不同的接运公交车站上车，乘客消耗等同的分配时间、换乘时间。因此，我们的目标是尽量减少乘坐时间，包括接运公交车时间以及轨道交通时间。为了简单起见，这里只考虑了两个目的地，分别为线路起点（o）和终点（d）。假设乘客可以分别在车站A、B和C进行换乘，如果在B站换乘所用的总出行时间小于在A站、C站换乘的总出行时间，那么，乘客将会选择在B站换乘轨道交通，也即接运公交—轨道交通的换乘站应该设在B站。由此构建模型。假设乘客位于i点，想要乘坐地铁从J站到达目的地[δk]。总时间是从站点J上车的所有线路的最短时间，A是所有轨道交通的站点的集合。

2.1 接运公交OD分布

存在n个公交站点，记为s1，s2，s3，...，sn，公交站点的OD矩阵[12]为

[oij=0o12…o1，mo120……           om，1……0]  。

矩阵中的元素表示：从起点（i）到终点（j）的人数，那么，第i个站点的出行需求记作：[di=j=1， j≠imoij]。

2.2 模型的建立

2.2.1 目标函数

一般地，接运公交的优化目标有：接运效率最大，最大的客运周转量，社会的总交通时间最小以及公交部门的经济效益最大等等。由于各目标是彼此相关的，且本文是对布设区域进行研究，在考虑OD分布的基础上对整体出行时间最小化进行计算，可以较大程度的符合实际，得到更好的优化效果，因此，建立的目标函数为乘客分别乘接运公交与轨道交通行驶时间之和的最小值，如下：

[min tj=tpiRj+tRjδk                      j∈A]， （5）

[tpiRj=lpiRjv1oij]， （6）

[tRjδk=lRjδkv2di]， （7）

[lpiRj=clij]， （8）

式中：[tpiRj]代表乘客乘接运公交出行时间;[tRjδk]代表乘客乘轨道交通出行时间;[lpiRj]代表乘客乘接运公交出行距离（km）;[lRjδk]代表乘客乘轨道交通出行距离（km）;[lij]代表从点i到车站j的最短距离（km）;c是非线性系数，此处取1.4;δk是出行目的地，k=1，2，即轨道的起讫点 OD。目标（5）代表所有乘客总出行时间（乘坐接运公交时间与乘坐轨道交通时间之和）;式（6）、式（7）分别为乘客乘接运公交、轨道交通出行时间的表达式;式（8）表示乘客乘接运公交的出行距离。

2.2.2 约束条件

1）出行长度

当人们的出行距离较短时，出于方便程度与出行时间的考虑，人们会选择常规公交直达，而不会选择接运公交换乘轨道交通到达目的地，同时，当人们的出行距离较长时，由于接运公交-轨道交通换乘出行成本小于选择直达公交的出行成本，人们大多会选择换乘，此时，出行距离大于等于边际出行距离。根据上面对于边际出行距离的讨论，得出条件

[lpiRj+lRjδk≥C1-C2-（Tv+Td）Eα-y（1-λ）Eβ1v2-1v1-δ]。 （9）

2）出行时间约束

在不考虑其他交通方式的前提下，考虑各个公交站点的OD分布情况对总出行时间的影响，为了保证总的出行时间最小，即所有乘客经过轨道—公交换乘从起点到达终点的时间。假设在j点换乘可以得到最小的耗费时间，即其余站点的出行时间均大于或等于此站点，即满足条件

[tj≤tr， （j≠r， r∈A）]。 （10）

2.3 求解算法

Step 1：初始化。根据一次吸引范围和二次吸引范围的定义，整个区域被划分为500 m × 500 m的单位网格。将每个网格顶点编号为m，分别为[p1，p2，p3，…，pm]。假设[Rj]代表轨道站点，总共有n站，编号[R1，R2，R3，…，Rn]。δk作为路线上的起点和目的地。用[Sj]作为站j的布局区域。

Step 2：设i = 1，k = 1。

Step 3：为站点 j 的布局区域创建满足性函数[Fj（pi）]。

Step 4：根据公式（5）～（8），计算[t1，t2，t3，…，tn]。

Step 5：设置[tj=mint1，t2，t3，…，tn]。

Step 6：根据公式（9），如果满足条件约束，则返回[Fj（pi）=1]，否则设置[Fj（pi）=0]。

Step 7：当k = 2时，执行下一步，否则k = k + 1，然后转到步骤3。

Step 8：当i = m时，执行下一步骤，否则i = i + 1，并转到步骤3。

Step 9：找出满足[Fj（pi）=1]的所有点。

3 算例

3.1 北京5号線基本现状

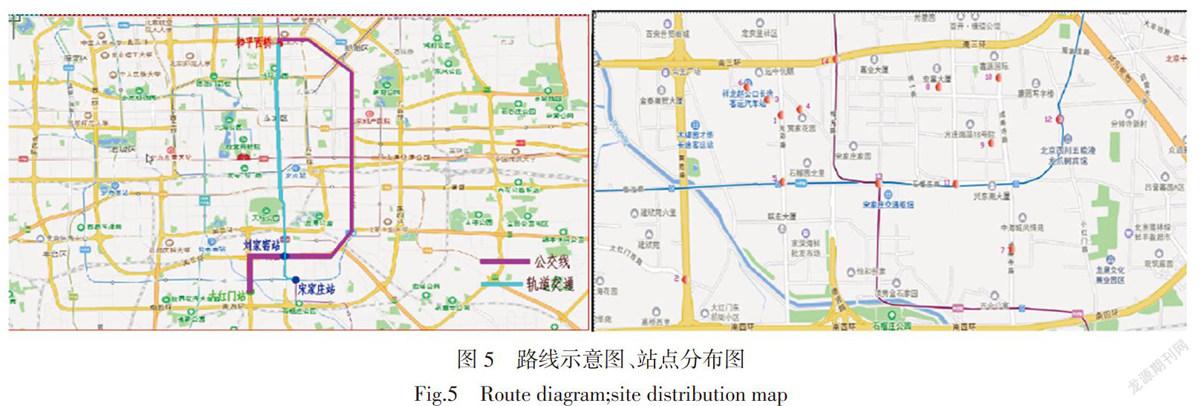
由于北京5号线已经建成并且运营，以北京地铁5号线为例对以上模型进行计算分析，北京地铁5号线（亦可简称“5号线”），是北京市的一条城市地铁线路，经过诸如天坛、东单之类的景区与商业区，是北京南城拥有的首条有着实际意义的地铁线路。该线首末站为宋家庄站与天通苑北站，线路全长共有27.6 km，设有23座车站。

3.2 举例分析

为了计算简便，本文以从大红门到和平西桥为例计算接运公交布设区域，以验证提出的模型和算法的准确性。假设大红门站附近的乘客需要到位于地铁5号线的和平西桥。

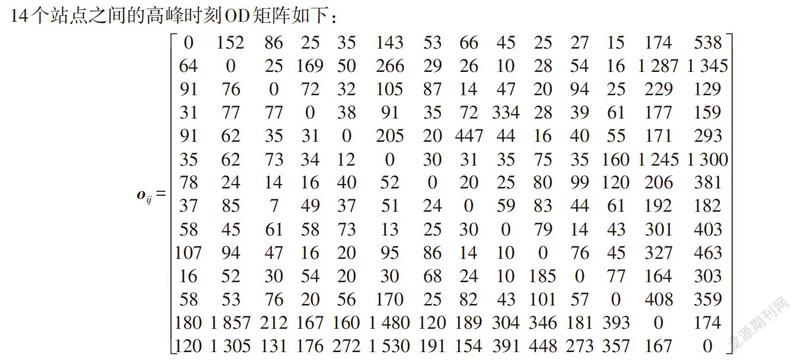
14个站点之间的高峰时刻OD矩阵如下：

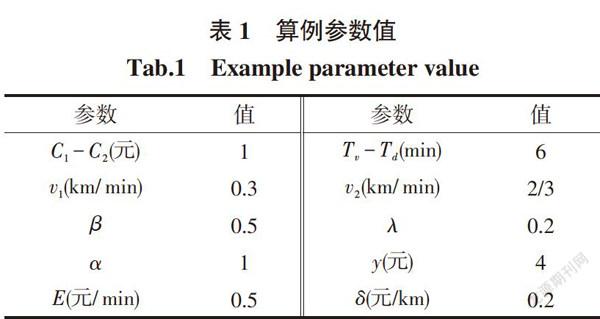
3.2.1 模型参数值标定

通过现场调查和分析，将相关数据结合在一起，对参数给出近似值。

根据薛兴建[7]的研究分析，在此非直线系数选择 c=1.4;由于轨道交通比直达公交更加舒适，量化是C-C=1元。北京市月人均可支配收入5 000元;北京市常规公共交通运行速度为v=0.3 km / min;北京地铁5号线的运行速度为v=2/3 km/min;北京常规公交票价：出行距离小于等于10 km时，票价为2元，大于10 km时，每增加1元能够多乘坐5 km。由此，本研究中，x = 2元，s = 10 km，[δ]= 0.2;地铁票价：6 km（含）内3 元;6 ～ 12 km（含）4 元;12～22 km（含）5 元;22～32 km（含）6 元;32 km以上每加1 元可乘20 km。

3.2.2 计算与分析

根据该算例结合边际出行距离计算公式（4）可以得出，边际出行距离为11.39 km。由本示例可知：行程距离超出11.39 km。因此乘客选择轨道交通与常规公交一次换乘比较合理。

实际情况表明：刘家窑、宋家庄均是地铁5号线上的站点，都能够到达和平西桥。由于本例方向宋家庄是始发站，宋家庄与刘家窑距离大红门相对较近，而其他换乘站点距离较远且大红门不在其影响范围内，上文分析[λ]的敏感性得出：人们乘坐公交车的运行距离越短，越容易换乘轨道交通。故而乘客可选择在刘家窑或宋家庄转乘轨道交通，再通过乘坐地铁五号线到达和平西桥。将各参数值带入公式（5），分别计算得出：乘客选择在刘家窑转乘时，所有行程时间为130 969.4 min，而宋家庄则为118 908 min。所以该乘客应该选择在宋家庄换乘，如果出发点与目的地改变，轨道交通换乘站点的选择也是如此。

结果接近实际调查数据。 事实上，北京在大红门和宋家庄之间建立了一条接运公交线，证明了该模型的结果是可靠的。

4 结论

基于以前的研究成果，特别是薛兴建研究，本文进一步完善了接运公交车布局区域模型。在计算边际出行距离的时候增加了乘客舒适度的影响，票价根据实际情况来确定。通过对居民收入水平、轨道交通票价以及[λ]的敏感性分析得出：为了鼓励出行者换乘，发挥接运公交与轨道交通的作用，应该尽量提高居民收入，在合理范围内，不要过于提高轨道交通票价，接运公交长度不宜设置过长，同时，政府需要发挥积极发挥作用，引导有较长的出行距离的乘客换乘轨道交通出行，从而发挥社会效益。

当居民的出行距离大于边际出行距离时，乘坐公共汽车从地铁转乘的综合行车费用低于乘坐直达公交车。基于最小化乘客消费时间的思想，考虑了OD分布的影响。根据实际情况重新选定了传统公共交通和城市轨道交通的运行速度以及票价，建立了接运公交车布局区域模型，结果符合实际情况。以后的研究可以在此基础上对接运公交进行更为具体的布设方案，比如发车间隔，时刻表方面进行优化计算。

参考文献：

[1]    PATTNAIK S B， MOHAN S， Tom V M. Urban bus transit route network design using genetic algorithm[J]. Journal of Transportation Engineering，1998，124（4）： 368-375.

[2]    KUAN S N，ONG H L，NG K M. Solving the feeder bus network design problem by genetic algorithms and ant colony optimization[J]. Advances in Engineering Software， 2006， 37（6）： 351-359.

[3]    许旺土， 何世伟， 宋瑞. 轨道交通接运公交发车间隔及票价优化模型[J].吉林大学学报（工学版），2009，39（6）： 1469-1474.

[4]    郭本峰，张杰林，李铁柱.城市轨道交通接运公交最优长度与线路布设研究[J].交通运输工程与信息学报，2012，10（4）： 74-81.

[5]    马宇红，陈闪，张琴，等.城市接运公交网络的设计与优化[J].西北师范大学学报（自然科学版）， 2017， 53（2）： 21-29.

[6]    YU Y， MACHEMEHL R B， XIE C. Demand-responsive transit circulator service network design[J]. Transportation Research Part E： Logistics and Transportation Review，2015， 76：160-175.

[7]    刘华胜，赵淑芝，朱永刚，等.基于有效路径的轨道交通接运线路设计模型[J].吉林大学学报（工学版）， 2015，45（2）：371-378.

[8]    建设部.关于优先发展城市公共交通的意见[DB/OL]. [2015-08-10]. http：//www.cin.gov.cn/city/other/2004031802.htm， 2004.

[9]    蒋冰蕾， 孙爱充.城市快速轨道交通接运公交路线网规划[J].系统工程理论与实践，1998，18（3）：130-134，139.

[10]  薛行健.城市轨道交通接运公交线网优化研究[D].长沙：长沙理工大学，2008.

[11]  袁润文.配合城市轨道交通的常规公交线网调整研究[D]. 北京：北京交通大学，2008.

[12]  张毅.轨道交通影响下的常规公交线网优化及其应用研究[D]. 成都：西南交通大学，2014.

[13]  夏辉.基于行人出行时间的轨道交通和常规公交协调研究[D]. 北京：北京交通大学，2014.

[责任编辑 杨 屹]