《找次品》教学设计

莫雨晴

【中图分类号】  G633.6             【文献标识码】  A   【文章编号】  1992-7711（2019）06-254-02

【教学内容】

义务教育教科书人教版《数学》五年级下册P112.113例1、例2

【教学目标】

知识技能：1. 积累利用天平原理解决“找次品”问题的数学活动经验;

2. 学会用直观的方式表示逻辑推理过程

数学思考：在观察、实验、猜想、推理中，发展思辨能力

问题解决：1. 体会“找次品”问题解决方法的多样性

2. 掌握“找次品”问题解决的思路以及最优化策略

情感态度：感受数学在日常生活中的广泛应用并体验问题解决的乐趣

【教学重难点】

重点：理解“找次品”问题解决的一般思路

难点：掌握“找次品”问题解决的最优化策略

【教学具准备】

教具：《找次品》微课视频、5瓶钙片、磁铁

学具：学生自制小圆片

【教学过程】

一、课前预习

（一）自学课本和微课。

（二）完成课前练习。

【设计意图：1、让学生对“找次品”问题有一个大致的了解，提高课堂学习的效率提高;2、通过做练习题，加强学生对于所学知识的记忆与理解;3、通过练习题完成情况的反馈，掌握学生对于“找次品”问题的认知程度，针对性地进行二次备课。】

二、课堂教学

（一）开门见山，引出课题

1.提问学生通过预习课本和微课，学到了什么？

【预设1】找次品

追问：什么是找次品问题？/是怎么找的？

引出关于天平的说明：不是真实的天平、没有用到砝码、是在心中想象出来的虚拟天平;利用的是天平的平衡原理进行推理

【预设2】从3瓶中找出次品要称1次

追问：你是如何从3瓶中找出次品的？

（1）邀请学生上台边演示边说，老师板书

（2）全班同学用双手当天平，利用小圆片模拟过程

（3）思考问题：为什么天平可能平衡也可能不平衡呢？

教师板书并小结：

如果只需要称一次，不需要每个都称;

称的时候要保证两边物品的数量要相等;称的时候因为是随机拿的两个，所以天平可能会出现两种情况，可能平衡也可能不平衡。

【预设3】从9瓶中找次品，保证能找出次品至少要2次

追问1：如何理解问题“至少保证能找出”？

追问2：如何称才能使称的次数最少？把9瓶分成了多少份？

追问3：为什么分成3分能使称的次数最少？——利用天平不仅可以对天平两端的物品进行判断，而且可以对没有称量的那一部分做出判断。所以如果我们把要称的物体分成三份可以使得每次称完之后将次品的范围缩小到原来的三分之一

教师板书并小结：

称一次只是可能找出，但是不能保证一定能找出;

找次品的一般推理过程：分——称——观察——推理。

【预设4】从11瓶中找次品，保证能找出次品至少要3次

追问：你是如何分的？——列举分成3份的方法并提问对应找出次品的次数

思考问题1：为什么都是分三份但是至少要称的次数会有一样也有不一样？

思考问题2：哪个更快找出次品，为什么？——引导学生发现哪种分法能在一次称完后，确定次品的范围更小。

教师板书并小结：要想找的次数少

能平均分成3份得要平均分像我们刚刚的9瓶分成（3，3，3）

不能平均分的要尽量每份尽量平均分像11瓶就分成（4，4，3）

這样做的目的都是为了称了一次之后将我们的范围缩得更小。

【设计意图：1.学生全班分享交流课前预习的学习成果，开门见山地引出课题，巩固学生对于“找次品”问题的认知;2通过不断地追问让学生进一步理解并掌握“找次品”问题的最优化策略是要把待测物品分成3份，每份尽量平均分”】

（二）运用策略，解决问题

1、提出问题：“要从243瓶钙片中找出一瓶次品，至少称几次保证能找出次品？”

引导学生化繁为简，先从较少数量的物品出发研究问题

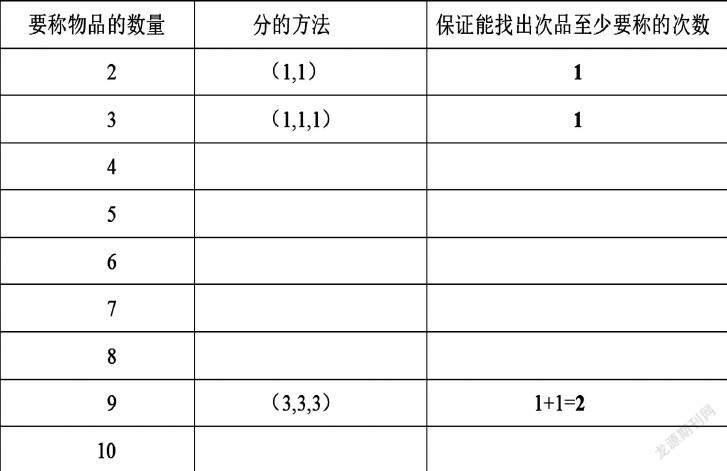
2.从数量为2～10的物品中找次品对应要称的次数

（1）小组合作完成表格

（2）小组汇报展示

（3）教师总结板书：注意引导学生利用已知数量要称次数解决新的问题

比如：将5瓶分成（2，2，1）我们考虑的是第一次不能找出次品，天平不平衡，次品就有可能在2瓶中，前面已经知道，从2瓶中找次品至少需要1次，所以从5瓶找次品保证能找出至少需要1+1=2次

【设计意图：

1. 通过从较大数量的物品中找出次品的问题，激发学生的探究欲望

2. 通过找出4瓶、5瓶、6瓶、7瓶和10瓶次品至少要称的次数，进一步掌握找次品问题的最优化策略，深化知识的巩固与理解

3. 为后面找出不同数量物品的次品对应的次数的规律做铺垫】

（三）拓展应用，深化问题

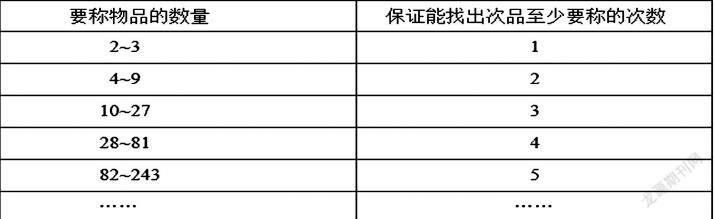
1.思考问题：至少称3次最多能从多少物品中找出次品？4次呢？

2.解决问题“从243瓶钙片中找出次品，至少称几次保证能找出次品？”

3.总结规律：课件展示图表

【设计意图：1、问题层层深入，拓展学生的思维2、在问题解决的过程中，体会数学的奥妙，获得学习成就感。】

（四）教师小结

1.邀请学生分享

同学们，你们今天学到了什么知识，有怎么的收获？

2.教师总结

我们这节课学会了如何在一堆看似相同的物品中利用天平原理找出质量不同的物品。问题解决可以按照：分——称——观察——推理的思路去分析，而且在从9个、11个物品中找次品的过程中，我们发现了称量前分的不同，至少保证能找到次品的次数也会不同，尽量分成3份才能使得次数最少。而且在课堂的最后同学们非常棒，通过自己的掌握的方法，整理出了从不同数量物品中保证能找出次品，对应的至少要称的次数。

希望同学们在课后能继续保持这种勤于思考，勇于解决问题的好习惯！