因子分析法与BP神经网络耦合模型对回采工作面瓦斯涌出量预测

徐刚 王磊 金洪伟 刘沛东

摘要：针对工作面瓦斯涌出量的影响因素众多且难以筛选的问题，提出了基于因子分析法与BP神经网络的工作面瓦斯涌出量预测方法。首先运用因子分析法对矿井瓦斯涌出量的影响因素降维处理，并筛选出3个主因子作为BP神经网络的输入端神经元，然后构建出基于BP神经网络的工作面瓦斯涌出量预测模型，并进行网络训练，最后对预测模型的可靠性进行检验。结果表明：因子分析处理后变量作用在影响因子上的权重得到了重新分配，并且变量的维数得以减少，错综复杂的变量关系被优化成3个主因子之间的线性组合关系，使得BP神经网络模型预测的瓦斯涌出量结果更合理，精度更高;工作面瓦斯涌出量预测值与实测值的相对误差均在5%以下，平均相对误差为3. 25%，误差波动范围小，稳定性较好，为复杂因素影响下的工作面瓦斯涌出量预测提供了一条新的思路。

关键词：瓦斯涌出量预测;因子分析法;因子选取;BP神经网络;网络训练

中图分类号：TD 712

文献标志码：A

文章编号：1672 -9315（2019）06 -0965 -07

DOI：10. 13800/j. cnki. xakjdxxb.2019. 0607

开放科学（资源服务）标识码（OSID）：

收稿日期：2018 - 12 - 06

责任编辑：杨泉林

基金项目：国家自然科学基金（ 51404189 .51404190）;陕西省自然科学基础研究计划（2015JQ51191）

通信作者：徐刚（1981 -），男，河南南阳人，博士，副教授，E-mail：408247198@ qq. com

O 引言

瓦斯涌出量预测是以煤层瓦斯含量、自然因素和开采技术因素为基础，并结合不同的方法对工作面瓦斯涌出量进行预测。矿井瓦斯灾害不仅影响煤矿安全生产，而且威胁井下人员生命和矿井设施安全，针对以上问题国内外学者对瓦斯涌出量提出了不同的预测方法。中国最早在90年代提出了梯度预测法预测瓦斯涌出量;1982年邓聚龙提出了灰色系统理论对矿井瓦斯涌出量预测[1];赫斯特于1965年提出R/S（Rescaled-range）分析法，该理论应用时间序列分析法预测瓦斯涌出量[2-3];1986年Rumelhart和McCelland的科学家小组提出BP网络（Back Propagation）模型，之后将BP神经网络模型应用于礦井瓦斯涌出预测[4];目前中国应用最广泛的是分源预测法，且已发展到实用化阶段[5];张子戌等提出瓦斯地质数学模型法对矿井瓦斯涌出量进行预测[6]。这些方法有各自的特点，但预测结果不能有效包含所有变量的信息，均是对瓦斯涌出量的影响因素进行量化而得到的结果，并且瓦斯涌出量一直处于动态变化过程，受诸多因素的影响，单一的瓦斯涌出量数据具有明显的波动性和信息不完全性[7]。

工作面瓦斯涌出量既是制定煤矿瓦斯灾害防治的重要依据，也是合理进行煤与瓦斯共采的关键参数[8]。由于我国煤层受多期构造影响，煤层瓦斯赋存规律极其复杂，导致影响瓦斯涌出的因素较多且影响程度存在较大差异，工作面回采过程中瓦斯涌出呈现出显著的不确定性、动态性和复杂性的特征[9]，影响因素和瓦斯涌出量之间没有明确的影响关系，难以用确定的数学模型表示，给瓦斯涌出量的预测带来了巨大的困难。因子分析法是一种信息处理方法，它既可避免信息量的重复，又可避免权重确定的主观性，能将众多变量所载的信息浓缩并转存到主因子上，使分析结果具有客观性和唯一性[10];而BP神经网络具有强大的非线性函数逼近能力、自适应学习能力，对不确定性问题的处理和非线性系统的预测有明显的优势[11-13]。因此，文中将因子分析法与BP神经网络预测模型相耦合，首先对影响工作面瓦斯涌出量的因素降维处理并归类，然后提取出主因子，将提取出的主因子作为BP神经网络的输入端神经元[14]，构建出矿井回采工作面瓦斯涌出量预测模型。该耦合模型可以充分利用各自的优势提高预测值的可靠性，对于科学合理地制定矿井瓦斯灾害防治措施具有重要意义。

1 工作面瓦斯涌出量影响因子的确定

1.1 因子分析法的基本原理及步骤

因子分析法是一种从变量群中提取共性因子的统计技术，能对多维变量进行简化降维和自优化处理[15 -16]，能够在众多变量中找出隐藏的具有代表性的因子，将具有共性变量归入一个因子，从而以较少的几个因子反映原数据的大部分信息，从而达到合理解释变量的相关性和筛选变量的目的[17]。

建立如下因子分析法的数学模型

1.1.1 原始数据标准化处理

为了消除各变量数量级的差异，使变量之间更具可比性，将数据标准化法处理，即Z-Score法，避免数量级给计算结果带来的影响。

1.1.2 因子分析的适用性检验

因子分析前首先对样本数据进行标准化处理，然后对样本数据是否适用因子分析法进行检验。一般采用Kaiser-Meyer-Olkin检验和巴特莱特（Bartlettde）球形检验。适用性检验的判定依据是样本变量的KMO（Kaiser-Meyer-Olkin）度量值和显著性概率Sig值，当KMO值大于0.6且显著性概率Sig值小于0.01时，样本达到了显著性水平，样本矩阵间有共同因素存在，适合进行因子分析。

1.1.3 因子的载荷及累计贡献率

1.1.4 公因子提取及旋转

公因子提取选用主成分中的相关性矩阵分析法，公因子提取的目的是用提取出来的较少几个因子解释样本原始变量，较少几个因子的累积方差覆盖了原始数据超过80%的信息，减少了样本变量包含的重叠信息，使不同变量的因子归属更加清晰。

公因子旋转选用最大方差法。具体方法是对公式（5）中的正交矩阵Γ左乘载荷矩阵A，得到的新载荷矩阵B，即

1.2 矿井瓦斯涌出量的影响因素分析

随着我国煤矿开采深度的不断增加，影响矿井瓦斯涌出量的因素越来越复杂，但其主要影响因素有自然因素和开采技术因素2部分组成。自然因素包括煤层与围岩瓦斯含量、煤层埋深、煤层厚度、顶底板岩性、地下水条件、工作面长度、大气压和温度等;开采技术因素包括采煤方法、通風压力、回采速度、日产量、工作面风量和回采率等。

崔家沟煤矿位于陕西省焦坪矿区，在回采过程中由于地质条件复杂瓦斯涌出规律不明显，瓦斯涌出量忽高忽低，多元线性回归等预测方法难以有效的适用，严重影响煤矿的安全生产。因此拟采用因子分析法与BP神经网络对工作面瓦斯涌出量进行预测，提高预测的准确度，以采取针对性的瓦斯治理措施。经过对工作面瓦斯涌出量的影响因素分析，考虑到崔家沟煤矿的大气压力、温度、通风压力、工作面风量及工作面长度等影响因素基本保持不变，对工作面瓦斯涌出量影响较小，所以这几个因素在建模时忽略不计;并且崔家沟煤矿煤层地质条件较好，工作面是厚煤层及特厚煤层，回采率变化较稳定，基本保持在85%左右，对瓦斯涌出量影响较小，在建模时忽略不计。最终确定出工作面的瓦斯涌出量与本煤层瓦斯含量、煤层厚度、煤层埋深、煤层倾角、日产量、邻近层瓦斯含量、煤层间距、回采速度等因素相关。通过分析矿井地质资料、矿井通风瓦斯报表及现场实测可得各相关影响因素的数据，用Xl - X8分别为上述相关影响因素，X9为绝对瓦斯涌出量，可得瓦斯涌出量及其相关影响因素统计表（表1）。

1.3 影响因子的确定

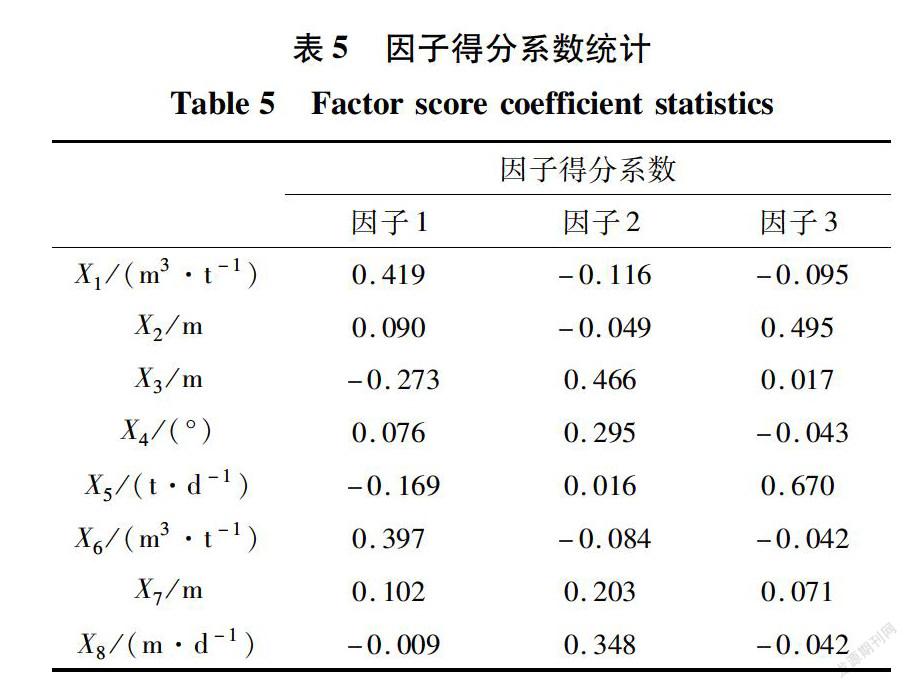
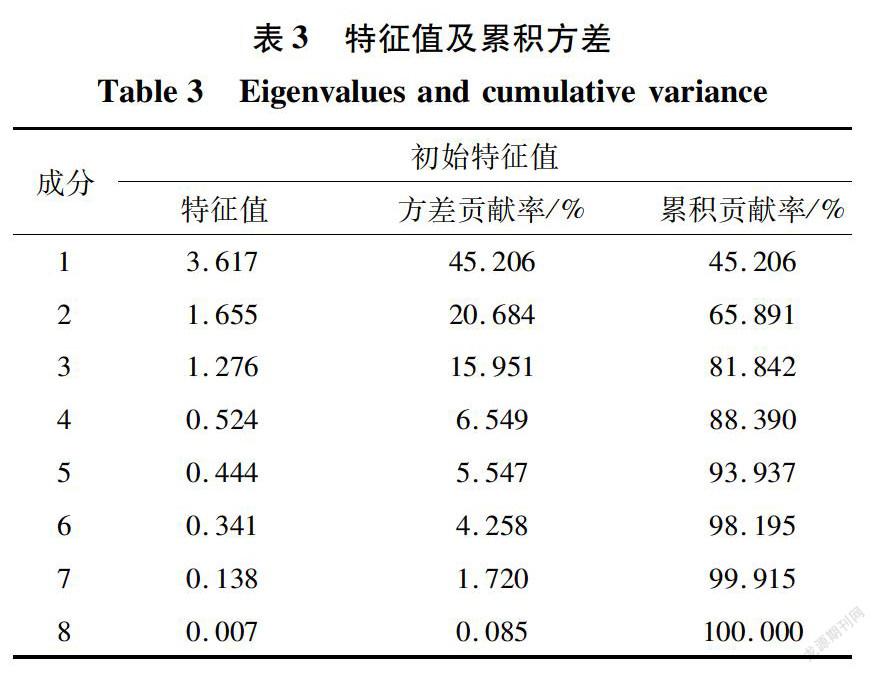
SPSS 20是大型一种数据处理及统计软件，内置有因子分析模块，可以对8个影响瓦斯涌出量的因素进行因子分析处理。因子分析前首先对原始数据进行标准化处理，然后根据因子分析法的具体步骤对样本数据进行分析，即可得到检验值表（表2）、特征值及累积方差统计表（表3）、旋转后成分统计表（表4）和因子得分系数统计表（表5）。

由表2可知，KMOf Kaiser-Meyer-Olkin）度量值为0. 631 >0.6，说明各样本变量之间具有较强的相关性。样本变量显著性概率Sig，值为0.000<0. 01，说明样本数量充足，且KMO值和Sig值都符合要求，说明原始变量适合进行因子分析并能实现降维简化。

由表3可知，前3个主成分的特征值大于1，并保留了超过80%原始变量携带的信息，较好的解释了变量之间的关系。现提取特征值大于1的成分作为影响因子，且前3个主成分的累计方差为81.842%>80%，而每个成分的方差所占比例为：45. 206%.20. 684%，15. 951%，由此确定出前3个因子为所提取的3个影响因子。

由表4可知，通过因子旋转使因子的归属更加清晰。旋转后成分中主成分1集中体现了：本煤层瓦斯含量和邻近层瓦斯含量对瓦斯涌出量的影响;将其解释为与瓦斯含量有关的影响因子;主成分2集中体现了：煤层埋深、煤层倾角、煤层间距、回采速度对瓦斯涌出量的影响;主成分3集中体现了：煤层厚度和日产量对瓦斯涌出量的影响。通过因子旋转将复杂无规律的影响因素分为3个主成分，减少了变量的维数。

由表5可知，经过因子分析后重新分配了变量作用在影响因子上的权重，降低了各指标之间的相关性，减少了相关性较差的变量对几个因子的同时影响，为瓦斯涌出量预测模型的建立奠定了基础。

由式（9）可得出因子得分式（10）。Fi=0.419X1 +0.090X2 -0. 009X8F2=-0. 16X1 -0. 049X2+ - +0. 348X8F3=-0. 095X1 +0. 495X2+ -0. 042X8 （10）

2 BP神经网络预测工作面瓦斯涌出量

2.1 BP神经网络模型的建立

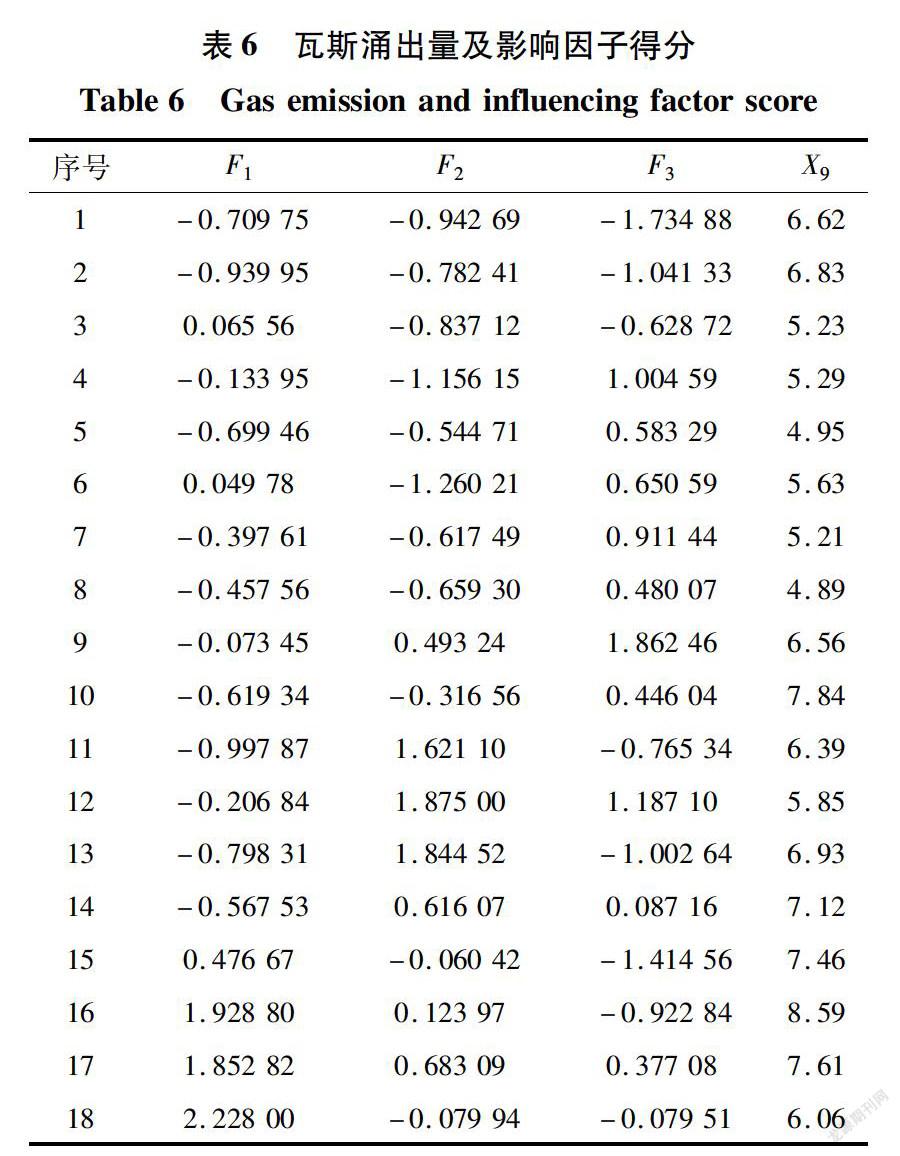
根据经验公式建立模型为3 -6 -1三层BP神经网络模型，其中输入端神经元节点数为3个，将因子分析得出主因子Fi，F2，F3作为BP神经网络模型的输入端神经元;隐含层节神经元点数为6个;输出端神经元节点数为1个，即矿井瓦斯涌出量值[22]。由式（10）计算出主因子F1，F2，F3总得分作为BP神经网络模型的输入端神经元（表6）。

2.2 BP神经网络训练和网络检验

采用MATLAB神经网络工具箱中traingdm（）函数对样本数据进行训练。其中tansig（）作为隐含层神经元的传递函数，purelin（）作为输出端神经元传递函数[23]。所训练时模型主要参数设定为：学习速率为0.01，训练误差精度为0.000 1.将表6中X9的前14组瓦斯涌出量作为训练样本，后4组瓦斯涌出量作为检验样本，用训练好的BP神经网络模型对后4组瓦斯涌出量进行预测，经过1 500次训练后函数收敛，可得训练结果及相对误差（表7）和神经网络最佳训练成绩（图1）。

2.3 与多元线性回归法比较

根据表1原始数据，用式（11）计算多元回归方程，使用Matlab软件得到煤层瓦斯含量与各影响因素之间的多元回归方程

y= a0+ a1X1+ a2X2+ …+ amXm

（11）

X9=8.973 +0. 707X1 -0.182X2 -0.002X3+0. 067X4 -0. OOlx5 -0. 097X6 -0. 327X +1. 283X8

多元回归方程的决定系数R2= SSwg/SStotal，这里R2=0. 688，可知该方程拟合较好，但精度不能满足工程要求。运用Matlab软件计算得到影响崔家沟煤矿2303工作面瓦斯涌出量的各因素相对误差结果（表7）。

由表7可知，采用多元线性回归法预测的瓦斯涌出量平均误差为8. 98%，最大误差达到13.4%.而因子分析法预测的瓦斯涌出量误差均在5%以下，平均误差为3. 25%，有效地提高了预测精度;综合对比2种方法，因子分析法对BP神经网络输入端变量进行了降维优化，预测值的可靠性较强，预测效果较好。

3 结论

1）提出了一种将因子分析法与BP神经网络耦合的工作面瓦斯涌出量预测方法。经因子分析处理后变量的维数减少，变量之间相互影响的程度降低，变量作用在影响因子上的权重重新分配，使神经网络预测模型的收敛速度更快，为BP神经网络模型预测工作面瓦斯涌出量奠定了基础。

2）采用因子分析法與BP神经网络相结合的瓦斯涌出量预测模型对后4组瓦斯涌出量值进行了预测和误差分析。结果表明瓦斯涌出量预测值与实测值的相对误差均在5%以下，平均相对误差为3. 25%，且误差波动范围小;而采用多元线性回归法预测的瓦斯涌出量平均误差为8. 98%，最大误差达到13.4%，误差波动范围较大，稳定性差。说明训练好的BP神经网络模型预测效果较好，因子分析法与BP神经网络相结合的工作面瓦斯涌出量预测方法是行之有效的。

参考文献（ References）：

[1] 王学萌，张继忠，王荣，灰色系统分析及实用计算程序[M].武汉：华中科技大学出版社，2001

WANC Xue-meng， ZHANC Ji-zhong， WANC Rong.Grev svstem analvsis and practical calculation program[M]. Wuhan： Huazhong University of Science and Tec- hnology Press.2001.

[2] 曾勇，吴财芳.矿井瓦斯涌出量预测的模糊分形神经网络研究[J].煤炭科学技术，2004，32（2）：62 - 65.

ZENC Yong， WU Cai-fang. Study on fuzzy fractal Neu-ralnetwork for prediction of gas emission in mine[ Jl.Coal Science and Technology ，2004 ，32（2）：62 - 65.

[3]

Donald L，Twcottl. Fractals and chaos in geology andgeophysics[M].Cambridge： Cambridge University Pre-ss.1997.

[4] 杨智懿，熊亚选，张乾林，工作面瓦斯涌出量的神经网络模型预测研究[J].煤炭工程，2004，35 （10）：73 -75.

YANC Zhi-yi， XIONG Ya-xuan， ZHANG Qian-lin. Pre-diction of neural network model for gas emission inworking face[J].Coal Engineering， 2004 ，35（ 10）：73 - 75，

[5] 何清.工作面瓦斯涌出量预测研究现状及发展趋势[J].矿业安全与环保，2016，43 （4）：98 -101.

HE Qing. Current status and development trend of gas-emission prediction in working face[J].Mining Safetyand Environmental Protection ，2016 ，43 （4）：98 - 101.

[6] 张子戌，袁崇孚，瓦斯地质数学模型法预测矿井瓦斯涌出量研究[J].煤炭学报，1999 ，24（4）：34 -38.

ZHANG Zi-xu，YUAN Chong-fu. Study on prediction ofgas emission in mine by gas geological mathematicalmodel method[J].Journal of China Coal Society， 1999，24（4）：34 - 38.

[7] 谷松，预测瓦斯涌出量的新方法[C]//瓦斯地质与瓦斯防治进展，北京：中国煤炭学会，2007.

GU Song.A new method for predicting gas emission[ C]//Progress in gas geology and gas control. Beijing：China National Coal Society， 2007.

[8] 张子敏，瓦斯地质学[M].徐州：中国矿业大学出版社，2009.

ZHANG Zi-min. Gas geology[M].Xuzhou： China Uni-versity of Mining and Technology Press，2009.

[9] 叶桢妮，侯恩科，段中会，等.郭家河煤矿回采工作面瓦斯涌出量预测[J].西安科技大学学报，2017，37（1）：57 -62.

YE Zhen-ni， HOU En-ke， DUAN Zhong-hui， et al.Pre-diction of gas emission from mining face in Cuojiahecoal mine[J].Journal of Xi' an University of Scienceand Technology ，2017 ，37（1）：57 - 62.

[10]于欧亚.基于因子分析法的传媒上市公司财务绩效评价研究[D].成都：西南交通大学，2016.

CAN Ou-ya. Research on financial performance evalua-tion of media listed companies based on factor analysis[D]. Chengdu： Southwest Jiaotong University， 2016.

[11]毕建武，贾进章，刘丹，基于SPSS多元回归分析的回采工作面瓦斯涌出量预测[J].安全与环境学报，2013 ，13 （5）：183 -186.

BI Jian-wu， JIA Jin-zhang， LIU Dan. Prediction of gas e—mission in mining face based on SPSS multiple regres-sion analysis[J].Joumal of Safety and Environment，2013 ，13 （5）：183 -186.

[12]郝天轩，宋超，基于模糊神经网络的煤层瓦斯含量预测研究[J].中国安全科学学报，2011，21（8）：36 - 41.

HAO Tian-xuan， SONG Chao. Study on prediction ofcoal seam gas content based on fuzzy neural network[J]. Chinese Journal of Safety Sciences， 2011 ，21（8）：36 - 41.

[13]魏春荣，李艳霞，孙建华，等，灰色一分源预测法对煤矿瓦斯涌出量的应用研究[J].采矿与安全工程学报，2013 ，30（4）：628 - 632.

WEI Chun-rong， LI Yan-xia， SUN Jian-hua， et al.Studyon the application of grey source prediction method tocoal mine gas emission[J].Journal of Mining and SafetyEngineering， 2013 ，30（4）：628 - 632.

[14]王春娟，冯利华，罗伟，等，基于主成分分析的BP神经网络对南京市水资源需求量预测[J].水资源与水工程学报，2012，23 （6）：6 -9.

WANG Chun-juan， FENG Li-hua， LUO Wei， et al.Pre-diction of water resources demand in Nanjing based onBP neural network based on principal component analy-sis[J].Journal of Water Resources and Water Engineer-ing，2012，23（6）：6 -9.

[15]

Lunarzewski L_ Gas emission prediction and recovery inunderground coal mines[J].International Journal ofCoal Ceology ，1998 ，35（1）：117 - 145.

[16]

Edward Jackson J.A user's guide to principal compo-nents[M].New York：A Wiley-Interscience Publica-tion。1992.

[17] Horn J L.A rationale and test for the number of factorsin factor analysis[J].Psychnmetrica， 1965， 30（2）：179 - 185.

[18]赵建军，贺宇航，黄润秋，等，基于因子分析法的边坡稳定性评价指标权重[J].西南交通大学学报，2015，50（2）：325 -330.

ZHAO Jian-jun， HE Yu-hang， HUANG Run-qiu， et al.Evaluation index weight of slope stability based on factoranalysis[J].Journal of Southwest Jiaotong University，2015 ，50（2）：325 - 330.

[19]

Johnson R A ，Wichern D W. Applied multivariate statis-tical analysis[M].New Jersey： Prentice-Hall， 2014.

[20]解素雯，基于主成分分析与因子分析数学模型的应用研究[D].淄博：山东理工大学，2016.

XIE Su-wen. Research on the application of mathemati-cal model based on principal component analysis andfactor analysis[D].Zibo： Shandong University of Tech-nology，2016.

[21] Noack K.Control of gas emission in undergound coalmines[J].International Journal of Coal Geology， 1998，35（1）：57 - 82.

[22]李樹刚，马彦阳，林海飞，等，基于因子分析法的瓦斯涌出量预测指标选取[J].西安科技大学学报，2017，37（4）：461 -466.

LI Shu-gang， MA Yan-yang， LIN Hai-fei， et al_Selectionof prediction index for gas emission based on factor a_nalysis method[J].Journal of Xi' an University of Sci-ence and Technology ，2017 ，37（4）：461 - 466.

[23]王生全，刘柏根，张召召，等，遗传算法的BP网络模型进行瓦斯涌出量预测[J].西安科技大学学报，2012 ，32（1）：51 - 56.

WANG Sheng-quan， LIU Bai-gen， ZHANG Zhao-zhao， eta1. BP network model of genetic algorithm for gas emis-sion prediction[J].Journal of Xi' an University of Sci-ence and Technology ，2012 ，32（1）：51 - 56.