基于小波分析的多波束测深系统的构建
2019-09-10王思凯李九奇
王思凯 李九奇

摘要:多波束系统的工作原理与传统的多波束回声测深仪工作原理类似,都是根据声波在水下往返传播的时间与声速的乘积得到距离,从而得到水深。不同的是多波束测深仪一般采用较宽的发射波束(8°左右)向船底垂直发射,形成多个具有不同指向角的波束,通常只发射一个波束而在接收时形成多个波束。除换能器天底波束外,外缘波束随着入射角的增加,波束在倾斜穿过水层时会发生折射,同时由于多波束沿航迹方向采用较窄的波束角而在垂直航迹方向采用较宽的覆盖角,获得整个测幅上精确的水深和位置。
关键词:小波分析;多波束;测深;系统测量
中图分类号:U675 文献标识码:A
1 多波束的形成
一个多波束在水中发射后,是球形等幅度传播,所以方向上的声能相等。这种均匀传播称为各向同性传播(isotropic expansion),发射阵也叫各向同性源(isotropic source)。显然,测深时是不能采用如此的声波的。采用发射基阵就可以产生各向异性的声波。f(t) = 2pft。相对于第一个基元的距离差,转换为相位差为其中Bi(θ)为第i个基元在角θ方向接收时的回波,则基阵接收的回波为其中si为加权系数。如果要求在一个时间片(time slice)里,由N个基元形成M个指定方向的波束,用矩阵表示为其中,Dij为接收角θj的波束时的第i个基元的相位差,为 。类似于傅立叶变换。
2 基于小波分析多波束
进行设定,即ψ(t)∈L2(R)(L2(R)表示实数空间,且平方可积),对其进行傅里叶变换后,可得(ω)。(ω)需满足以下限定条件。然后,通过对基本小波ψ(t)(或称之为母小波)进行伸缩和平移,从而得出一个小波序列。这时的小波函数就是离散小波。相应的离散小波变换为:特殊的,取a0=2,b0=1,可以得到二进小波:在应用过程中,为使得小波变换的计算更加有效,所构造的小波函数一般都具备正交性。
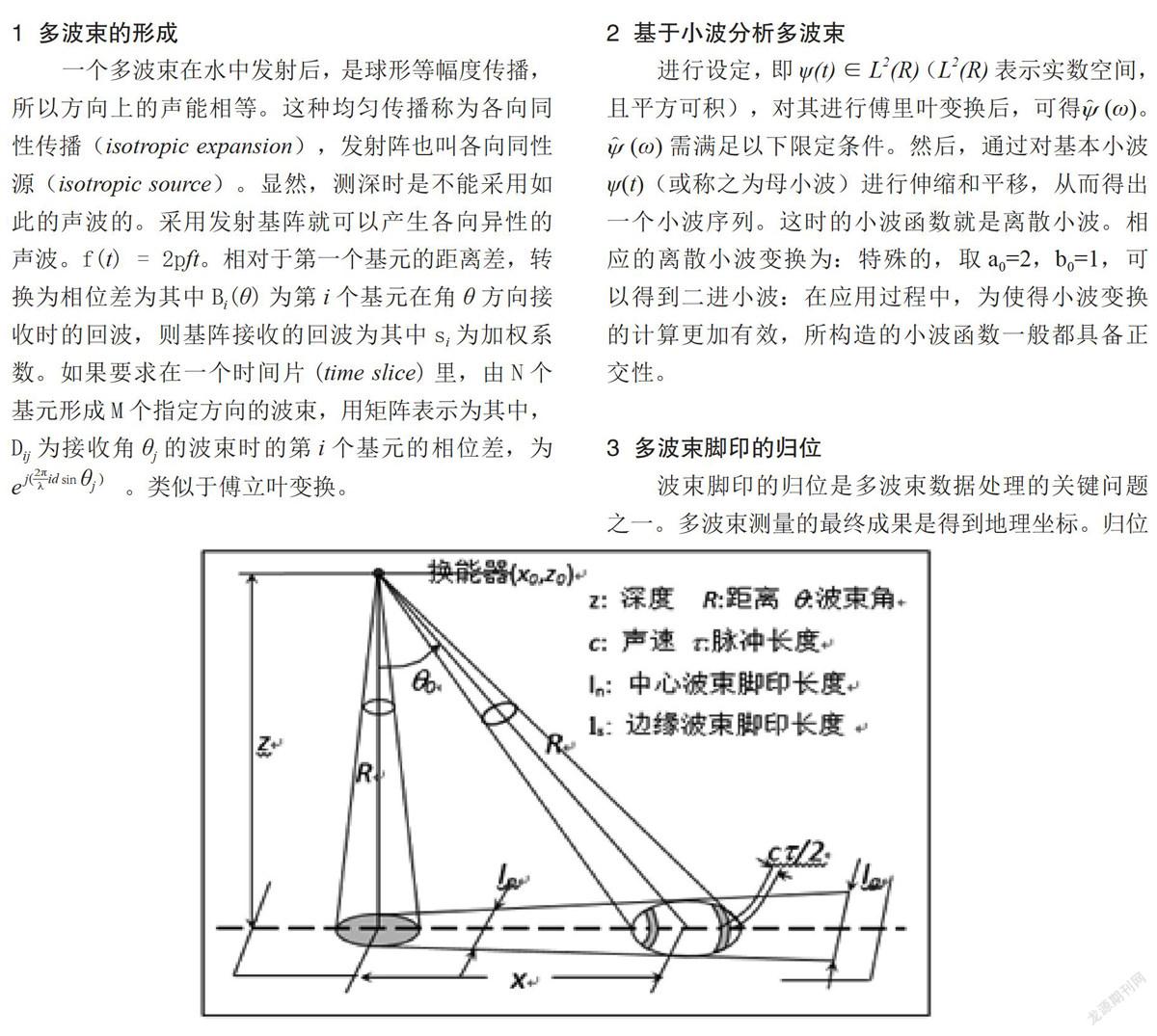
3 多波束脚印的归位
波束脚印的归位是多波束数据处理的关键问题之一。多波束测量的最终成果是得到地理坐标。归位过程包括根据上述讨论和假设,波束脚印的计算模型可表达为:将波束的实际传播路径进行微分,则波束脚印在船体坐标系下的点位(x,y,z)可表达为:
其一级在连续小波中,考虑函数此处b∈R,a∈R+,且a≠0,ψ是容许的。为便于计算,离散条件下,始终令a为正值,此时相容性条件即C意为与信号无关的常量。
Step1:设训练多波束集为X,多波束共分s类;
Step2:求多波束集X中多波束的最大模,将X中的多波束点依次按的变换方式投射到中心在原点,半径为R(R>r)的球面上,投射后的多波束集仍然以X表示;
Step3:求投射后多波束集X所对应的P(t),I(t),其中t=1,2……s,令初始值j=1,t=0,Ej′=Ø;
Step4:令 t←(t+1)mods,判断t是否为0,若是,令t=s,进入Step5;否则直接进入Step5;
Step5:判断P(t)是否为空,若否,即P(t)≠Ø,随机选取P(t)中的一个多波束点xk,进入Step6;若是,即P(t)=Ø,则继续判断集合X是否为空,若是,算法结束;若否,返回Step4;
Step6: 令
Step7:作以xk为球形领域中心,阈值为θ的覆盖Cj,令Cj∩P(t)=E ,判断Ej′是否为Ej的真子集,若是,进入Step8;否则,恢复原有的参数,进入Step9;
Step8:Ej′← Ej,求集合Ej中多波束点的重心xk′,再将xk′投影到超球面上,仍然以xk′表示投影后的点,令xk← xk′,返回Step6;
Step9:求xk的平移点xk′,将xk′投影到超球面上,仍然以xk′表示投影后的点,令xk← xk,根据Step6的计算方法求出以xk为球形领域中心,阈值为θ的覆盖Cj,令Cj所覆盖的所有多波束点的集合为Ej,判断Ej′是否为Ej的真子集,若是,返回Step8,否则,恢复原有参数,集合X←X/Cj,令P(t)←P(t)/E(j),I(t)为P(t)中多波束的标号的集合,j←j+1,返回Step4。
4 多波束测深
多波束系统主要由三个部分组成。第一部分是多波束的主系统,主要包括换能器阵列测量传感器和测量水柱声速剖面的声速仪;第三部分是数据存贮和后。
5 换能器的物理构成
换能器是用来作为电声能量转换的重要器件。通常把电能转换成声能的器件称为发射换能器,把水下声能转换成电能的器件称为接收换能器(或水听器),许多主动声纳中采用同一的换能器兼作发射和接收。
多波束优化问题中各单目标函数要求不一,有的要求极大值,有的要求极小值,有的要求一个合适值,为了反映这些要求的不同,引入功效函数di,其值即为功效系數,规定di∈(0,1),当fi满意时,di=1;fi不满意时,di=0;请他情况取0-1之间的的数。这样组成评价函数,d=1则最满意,d=0则有不符合要求的f。
系数di的确定:先求出区间上各个目标函数的最大值fi max和最小值fi min ,
在n个子函数中,当某个子函数的值越大,功效系数越小时用公式求其功效系数; 反之用公式求系数。功效系数法的基本思想是先按各子目标值的优劣分别求出其对应的功效系数,然后再构造评价函数
max f(X)= 便可转化为单目标优化问题。
6 多波束测深底部检测单元
在一个发射接收周期(ping)内,波束形成采用的FFT处理方法中的数据可表示为矩阵的形式,设一个周期内包含M个时间片(time slice),每个时间片分别表示为t1,t2,…,tM,相对的时间周期起点为t0。设有N个波束,每个时间片则可观测N个幅度值,θ1,θ2,…,θN,如图1所示。这样,每个幅度极大值对应另外两个数据:角度和时间。这3个数反映了波束发射到接收的过程,以击中(hit)表示,即每个击中用这3个数据表示。表示为θB和tB。为了问题的简化,本文没有考虑姿态补偿。在所有负指数值WNkn的值全部已算好的情况下,要计算x(k),我们需要n负乘法和n-1复数加法。为了计算所有的nx(k)点,n2复乘子和n(n-1)次是复杂的。也就是说,计算量与n2成比例。FFT的基本思想是:用大量的十进制数值多波束测深系统算法边界条件组合分解数值多波束测深系统算法边界条件,从而减少算术运算量。WN因子具有以下两个特点,数值多波束测深系统算法边界条件运算可以尽可能分解为DET运算。利用这两个性质,可以使数值多波束测深系统算法边界条件运算中有些项合并,以减少乘法次数。
7 結论
多波束测深系统的回波检测方式有两种,振幅检测和相位检测。当入射角小时,回波幅度高,持续时间短;当入射角变得十分大时,回波幅度低且持续时间长,但波束间的相位差变大,故振幅检测对于中间波束传播时间的检测具有较高的精度,而对边沿波束的检测精度较差,而相位检测正好相反。精密多波束测深系统利用相位检测用于边沿波束检测,振幅检测用于中间波束检测,由系统取舍。这样,在可保证每个波束检测精度的同时,又可保证整个波束的检测精度一致,从而达到波束旅行时高精度测定的目的。
参考文献
[1]Liu S, Jiang W, Jing W. Fault diagnosis based on characteristics of the vibration energy on the hydraulic pump[C]// International Conference on Mechanic Automation & Control Engineering. 2010.
[2]Ishikawa T, Ishigame R, Matsunami M, et al. Analysis and failure diagnosis of squirrel-cage induction motor with broken rotor[C]// International Conference on Electrical Machines & Systems. 2013:292-297.
[3]Jiang A, Li X, Wang W, et al. Misfire failure diagnosis of engine based on wavelet analysis[J]. Transactions of the Chinese Society of Agricultural Engineering, 2007, 23(4):153-157.
[4]Jinru L, Yibing L, Keguo Y. Fault diagnosis of piston compressor based on Wavelet Neural Network and Genetic Algorithm[C]// World Congress on Intelligent Control & Automation. 2008.
[5]Yuan L, Hu J, Huang J, et al. Fault Diagnosis on Slipper Abrasion of Axial Piston Pump based on Extreme Learning Machine[J]. Measurement, 2018, 124.
