基于边界条件和突变条件确定内力方程的一种方法

张宏学 姚卫粉

摘要：材料力学是理工科的专业基础课，能直接应用于工程实际，而杆件内力图是材料力学的核心内容，尤其是弯矩图，如何让学生快速、准确地绘制杆件内力图尤为重要.本文以弯扭拉组合变形杆件为研究对象，基于空间任意力系的平衡方程和微元法思想，建立了各种基本变形杆件的分布载荷和内力之间的关系，并给出了基本变形杆件的边界条件和突变条件.提出了确定内力方程的一种新方法，结合算例给出了详细的过程.与传统方法相比，该方法的优点是不需要预先求解杆件的约束反力.课堂教学效果表明，学生更偏向于利用该方法确定内力方程和做内力图，准确率高.

关键词：内力方程;内力图;边界条件;匹配条件

中图分类号：O302  文献标识码：A  文章编号：1673-260X（2019）07-0023-04

杆件内力图能够清晰地反映杆件内力随横截面位置变化的关系，同时也能确定杆件最大内力的数值及其所在截面的位置，即确定杆件危险截面的位置，为杆件强度计算提供依据.梁的弯曲是材料力学课程的核心内容，也是应力应变状态、组合变形、能量法、超静定结构等内容的基础，而梁的剪力图和弯矩图是梁的弯曲的核心内容[1].由此可见，杆件内力图在《材料力学》课程中具有举足轻重的地位，让学生熟练掌握杆件内力图的绘制并应用到工程实际至关重要.

绘制内力图，是公认的“材料力学的看家本领”，也是考核材料力学教学质量的一个重要方面[2].目前，《材料力学》[3-4]课程中杆件内力图常用的绘制方法有两种：一种是根据内力方程绘制内力图;另一种是简易法作图，即根据载荷集度和内力之间的微分关系以及积分关系绘制内力图.根据内力方程绘制内力图学生易于掌握，但列内力方程的过程较为复杂，容易出错;而简易法作图方法简单，但部分学生很难掌握.从历年教学和考试情况来看，学生在做杆件的内力图时，尤其是剪力图和弯矩图，更喜欢列剪力方程和彎矩方程作剪力图和弯矩图.无论采用哪一种方法绘制杆件的内力图，首先需要列平衡方程求解杆件的约束反力.

本文以弯扭拉组合变形杆件为研究对象，基于空间任意力系的平衡方程和微元法思想，建立拉压杆上的分布载荷和轴力间的关系、圆轴上的分布载荷和扭矩间的关系、梁上的分布载荷和内力间的关系.然后，提出了确定内力方程的新方法.最后，结合拉压杆、圆轴、梁的算例详细介绍了确定内力方程（不求解约束反力）的详细过程.

1 载荷集度和内力间的关系

如图1所示杆件，在外载荷作用下产生弯扭拉的组合变形.以杆件轴线为x轴，y轴向上为正.分布载荷的集度a（x）、m（x）、q（x）是x的连续函数，且规定a（x）向左为正、分布力偶的集度m（x）的矢量方向向左为正，q（x）向上为正.在距原点为x处，从杆件中取出长为dx的微段，如图2所示.由于杆件产生弯扭拉的组合变形，因此杆件左边截面上有轴力FN（x）、扭矩T（x）、剪力FS（x）和弯矩M（x）;由于分布载荷的影响，微段右边截面的轴力、扭矩、剪力和弯矩相对于左边截面的这些内力有相应的增量，因此右边截面的轴力、扭矩、剪力和弯矩分别记为FN（x）+dFN（x）、T（x）+dT（x）、FS（x）+dFS（x）和M（x）+dM（x）.微段两边截面上的内力均取正值，且所取微段内无集中力和集中力偶的作用.

对微段列平衡方程，∑Fx=0、∑Mx=0、∑Fy=0和∑Mz=0，得：

dFN（x）/dx=a（x）   （1）

dT（x）/dx=m（x）   （2）

dFS（x）/dx=q（x）  （3）

dM（x）/dx=FS（x）  （4）

式（1）-（4）分别表示轴力和载荷集度间的微分关系、扭矩和载荷集度间的微分关系、剪力和载荷集度间的微分关系以及弯矩和剪力间的微分关系.《材料力学》教材已经推导了载荷集度、剪力和弯矩间的微分关系，即式（3）和式（4）.《材料力学》教材针对式（3）和式（4）已得到一些推论，在此不再叙述.下面分析式（1）和式（2）.

在杆件的某一段内，当a（x）=0时，由dFN（x）/dx=a（x）=0可得，杆件此段内的轴力FN（x）=常数，轴力图是平行于x轴的直线;在杆件的某一段内，当a（x）=常数时，由式（1）可知该段杆件的轴力是关于x的一次函数，轴力图是一条斜直线.

在杆件的某一段内，当m（x）=0时，由式（2）可知，杆件此段内的扭矩T（x）=常数，扭矩图是平行于x轴的直线;在杆件的某一段内，当m（x）=常数时，由式（2）可知该段杆件的扭矩是关于x的一次函数，扭矩图是一条斜直线.

如果已知杆件在x处的内力，那么就能确定式（5）-式（8）中的积分常数，从而确定了杆件的内力方程，相应的内力图也就容易绘制了.本文根据杆件的边界条件和突变条件确定积分常数，确定积分常数的相关方程称为边界条件.表1列出了梁在不同约束处剪力和弯矩的情况.

拉压杆轴力图和圆轴扭矩图的绘制较简单，此处不再详述.下面将详细叙述利用该方法绘制剪力图和弯矩图的方法.与教材上常用的两种绘制剪力图和弯矩图的方法相比，通过该方法绘制剪力图和弯矩图，不需要求解梁的约束反力.如果梁在某些约束处的约束力已知，那么也可通过这些约束力确定积分常数.

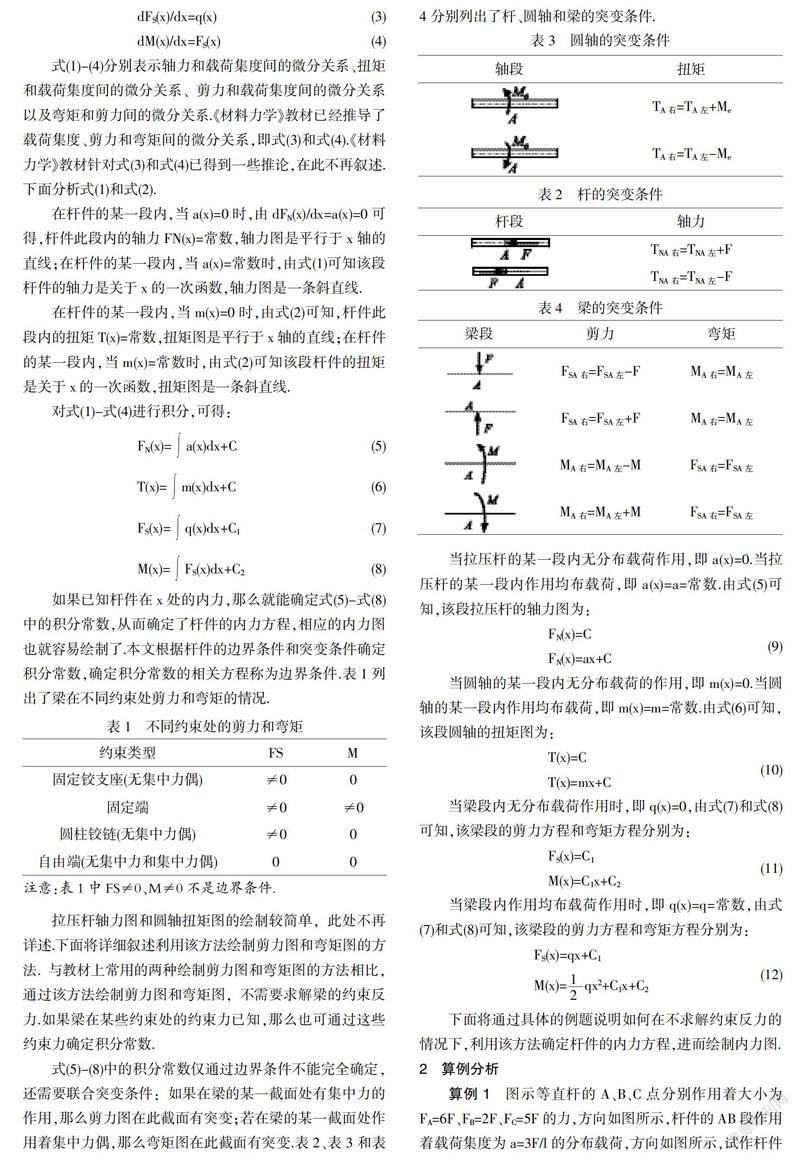
式（5）-（8）中的积分常数仅通过边界条件不能完全确定，还需要联合突变条件：如果在梁的某一截面处有集中力的作用，那么剪力图在此截面有突变;若在梁的某一截面处作用着集中力偶，那么弯矩图在此截面有突变.表2、表3和表4分别列出了杆、圆轴和梁的突变条件.

上述3个算例表明，利用该方法绘制杆件内力图的优点有：（1）不需要预先求解杆件的约束反力;（2）易于学生理解和掌握;（3）结合各种基本变形杆件的突变条件可以检查内力图的正确性.

3 结论

本文以产生弯扭拉组合变形的杆件为例，建立了弯扭拉组合变形杆件的内力与分布载荷之间的关系.并提出了确定杆件内力方程的一种新方法，结合算例给出了详细的过程，得到如下结论：

（1）根据内力与载荷集度之间的微分关系，分析了各种基本变形杆件在无分布载荷作用和均布载荷作用下内力图的形状.

（2）利用本文提出的方法确定杆件内力方程以及绘制内力图的优点主要有：不需要求解杆件的约束反力;学生容易理解和掌握;利用边界条件和突变条件能检查内力图的正确性.

（3）课堂教学效果表明，学生更偏向于利用该方法确定内力方程并绘制内力图，且准确率高.

参考文献：

〔1〕徐志军，原方.工程实例在建筑力学课程教学中的应用[J].力学与实践，2018，40（6）：700-703.

〔2〕范钦珊，尹雅俊，唐静静，等.改革教学，创新教学——“材料力学”课堂教学改革实践与体会[J].力学与实践，2018，40（5）：543-549.

〔3〕刘鸿文.材料力学（Ⅰ）（第5版）[M].北京：高等教育出版社，2010.

〔4〕孙训方，方孝淑，关来泰.材料力学（Ⅰ）（第5版）[M].北京：高等教育出版社，2013.

〔5〕严圣平，巫静波，陈启东，等.工程力学[M].北京：高等教育出版社，2013.