基于光滑粒子流体动力学方法的溃坝水流模拟

刘慧玲 李海桥

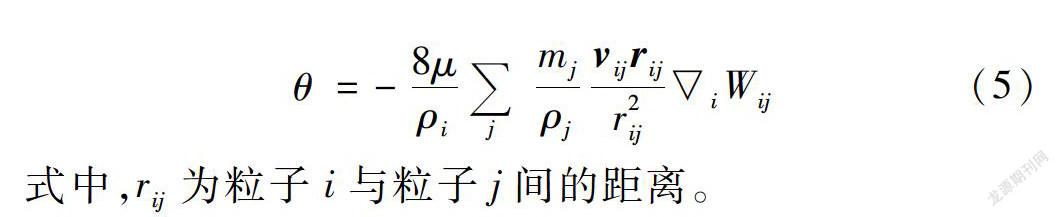
摘要：受全球气候变暖的影响，由极端天气引发的类似溃坝等问题发生的概率大大增加，深入研究溃坝水流的水动力特性势在必行。在分析光滑粒子流体动力学基本原理的基础上，提出了一种改进的边界处理方法，即将接近壁面的流体视为层流，在耦合动力边界附近引入层流黏性近似边界层理论。采用该方法对溃坝水流进行数值模拟，将SPH数值模拟得到的外轮廓、自由液面高度以及压力与实验结果进行了比较和分析。结果表明：改进的边界处理方法较完整地得到了水流与壁面相互作用而产生的多种复杂的物理现象，其外部轮廓与实验非常吻合;自由表面融合过程中液面间冲击的能量耗散会导致融合后的液面高度存在一些差异;不同监测点处压力随时间的变化基本落在置信区间之内。数值模拟结果与实验结果吻合度较高，验证了改进方案的可靠性和计算结果的准确性。

关 键 词：溃坝水流模拟; 自由液面; 耦合动力边界; 光滑粒子流体动力学（SPH）

溃坝通常指由自然灾害或人为因素引起的蓄水库围堰突然坍塌，造成人类生命、生态环境和生产经济巨大损失的灾害性事件。随着气候变暖的影响，极端天气出现的概率越来越大，由极端天气导致的类似于溃坝问题出现的概率也大大增加，给人们的生产生活带来了极大影响。研究溃坝水流的动态演变过程有利于理解洪峰水动力传播特性，从而为沿岸防灾减灾策略的制定提供科学依据。因此，对溃坝问题的探索具有显著的科学研究意义和工程应用价值[1]。

目前对溃坝问题的研究主要有3种方法：理论分析、数值模拟和模型实验[1-2]。早期对溃坝问题的研究主要以理论分析为主，但理论研究通常局限于比较简单的情形。近年来，随着测试技术的不断更新，溃坝问题的实验研究也从简单逐步趋于复杂[2-4]，Lobovsky等对溃坝实验做了100次的重复实验[2]，由于该实验数据详实，受到学术界的高度关注[5-7]。但是由于实验初始条件存在一定的随机性，100组实验数据仅展示了液面高度、监测点压力等重要动态参数的变化趋势[8-10]，也未能给出经验或半经验公式[11]，这也说明目前的实验操作水平依然存在很多局限性。近些年来，随着计算机技术的飞速发展和偏微分方程求解方法的改进，诸多数值计算方法广泛地应用于对溃坝问题的数值研究中[2-4，12-14]，并逐步将溃坝问题作为一个经典的数值验证算例。

由于溃坝问题伴随着复杂的自由表面演化和流体大变形的强非线性流体运动过程，利用拉格朗日型网格方法，如有限元法（FEM）等处理流体域的大变形时依然会遭受网格的畸变和缠结等因素影响，使计算精度降低和计算成本增加;欧拉型网格方法，如有限差分法（FDM）、有限体积法（FVM）在追踪复杂自由表面的演化过程时还存在一定的限制[15-16]，虽然VOF[6-7]，Level-set[17]，尤其是耦合VOF和Level-set的方法能较好地模拟该类问题[18]，但对网格精细程度要求依然很高。而无网格法，尤其是拉格朗日型的无网格方法恰好避免了上述问题，在涉及复杂自由表面演化的非线性流动预测中应用越来越广泛，其中最典型的是光滑粒子流体动力学（Smoothed Particle Hydrodynamics，SPH）方法[15-16，19-20]。SPH方法作为一种纯粹的粒子方法，具有完整的拉格朗日粒子性质，在处理伴随自由表面演化过程的大变形问题中，既能表征自由表面属性，又能准确描述流体的输运过程，表现出独特的优势。

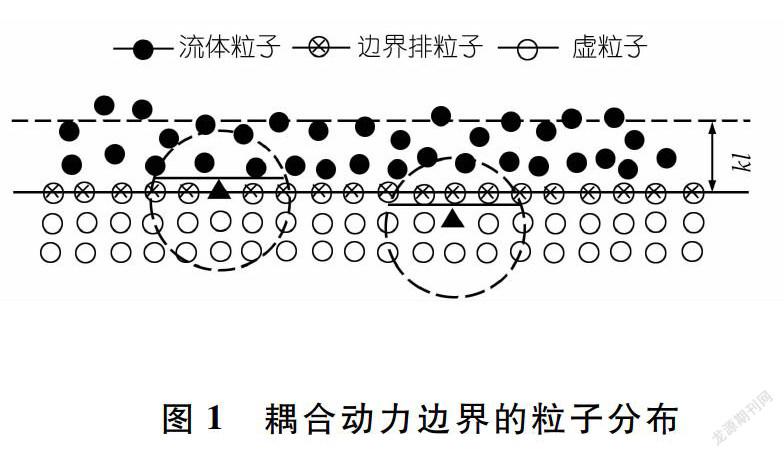
在以往的溃坝问题数值模拟过程中，固壁边界的数值处理方法对计算精度有非常重要的影响[13]。而在真实的流体流动过程中，在固壁边界附近有明显的边界层，边界层的厚度与主流区域的紊乱程度相关，但在边界层区域均表现出层流流动的特征。目前的溃坝流动实验研究中，实验装置均是规则的玻璃容器，表面较光滑，且溃坝水流还没有发展到整个流体区域为湍流的程度，根据边界层理论，此时的边界层主要为层流边界层。本文在计算过程中，将接近壁面的流体视为层流，加入层流黏性来近似概化黏性底层和边界层，计算溃坝流动，并与实验研究进行对比。

1 光滑粒子流体动力学

1.1 基本原理

光滑粒子流体动力学（SPH）是一种纯拉格朗日型无网格粒子方法，它使用一组粒子离散和代表所模拟的介质（流体或固体），并且基于粒子体系近似和计算介质运动的控制方程。然而不同于一般无网格方法，SPH方法中粒子不仅用于计算场变量与近似控制方程，同时也代表介质系统，具有诸如密度、压力、速度、内能等宏观物理量，相当于物质点，并且能够伴随介质的运动以当地速度移动。根据SPH方法的基本理论，其控制方程离散为[15，20] dρidt =jmj（vi-vj）·iWij

本文应用层流黏性对边界处进行近似边界层理论处理，更加接近实际物理情况，与传统的单一排斥力等边界处理方法相比，减缓了流体与壁面冲击过程中的数值振荡，最明显的就是降低了冲击时刻的压力梯度，使得数值解更加光滑。该黏性模型既能保证线动量和角动量的守恒性，能量的耗散也较小，并且具有较好的层流模拟能力。在边界层处选用该模型，并对边界周围的粒子运动进行修正，能最大程度降低黏性力模型造成的数值影响。另外，在流体计算过程中，边界层内应用黏性方程（5）是为了更加接近边界层理论，而对于主流区即非边界层内的流体则采用了SPH常用的人工黏性来处理流體。

本文在进行边界处理时，将接近壁面的流体视为层流，在耦合动力边界附近引入层流黏性近似边界层理论，有利于提高溃坝问题的数值模拟精确度，这将在下一节的模拟计算中得到验证。

2 溃坝问题的数值仿真

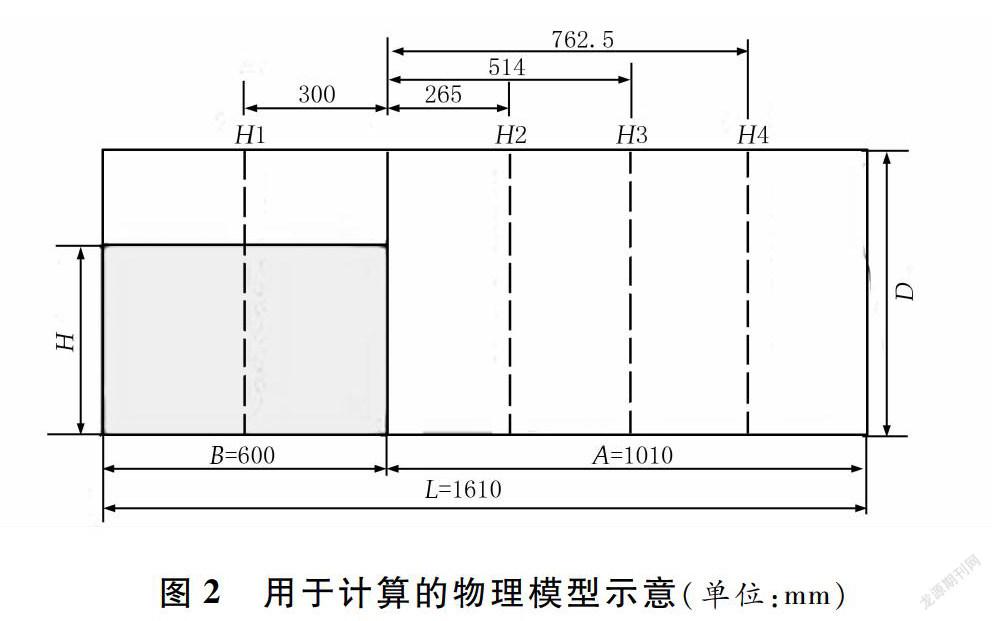
为了与实验更好地比较，本文计算的物理模型与文献[2]的实验模型相一致，如图2所示。容器长度为1 610 mm，高度为600 mm，初始时水体的尺寸为600 mm×300 mm，水体宽度为600 mm，高度为300 mm。H1～H4是观察水体实时表面高度的具体位置。

2.1 流體外部轮廓比较

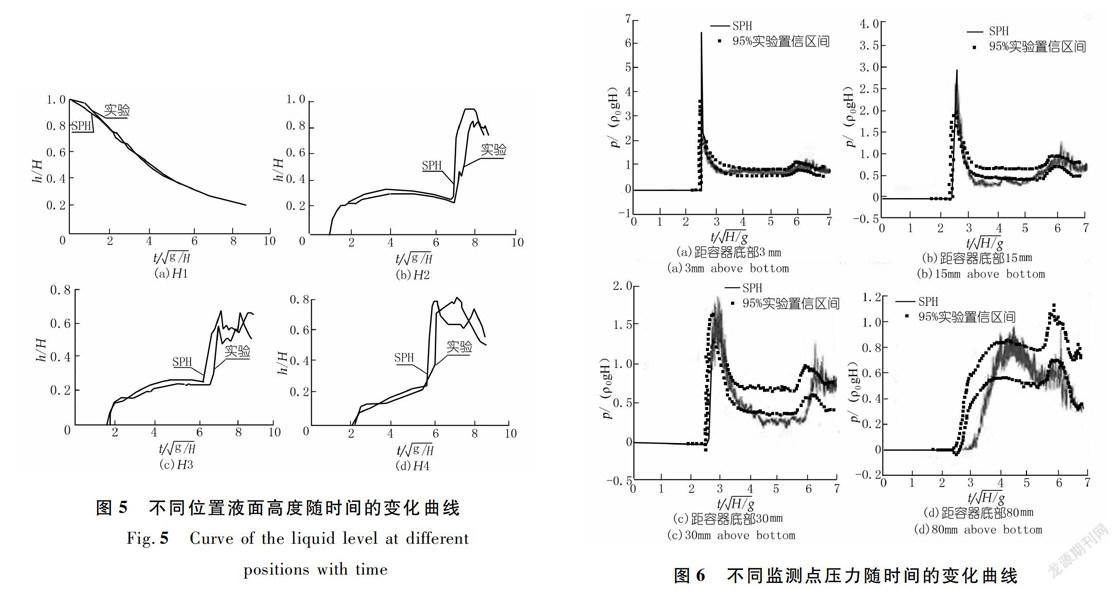
为了更系统地和文献[2]中的实验结果进行比较，本文对流体外轮廓的高度和时间进行相同的无量纲化处理，无量纲液面高度的h*表达式为h*=h/H，无量纲时间t*的表达式为t=tg/H。此处h为实时液面高度，H为初始时刻的液面高度。图3给出了不同时刻实验与SPH计算的外部轮廓图，以及不同时刻相对压力的分布情况，其中时间后面括号内的数值是相对应时刻的无量纲时间。从图中可以看出，在不同时刻，SPH计算结果的轮廓和实验的轮廓基本吻合，尤其在t=5.851 6和t=6.671 1时，液体的飞溅现象明显，也基本和实验中飞溅现象的轮廓相一致。图3中右侧彩色云图展示的是不同时刻流体的相对压力的分布情况，从流场的压力分布可以看出，在不同时刻，压力分布光滑、连续。图4所示的是t=4.931 0时刻右侧拐角处的流场图，从流场的具体分布可以看出，流场顺滑，并且明显地展现出流体流动方向改变而产生的涡，在边界附近，流体的速度相对较小，表明了近似边界层的修正起到了明显作用。

结合图3可以明显的看出：在水流冲击右侧壁面后，随着水流的翻卷并倾覆，与主流区域相融合之前，不同位置液面高度随时间的变化与实验吻合相当好。但当上涌的水流与主流区域相融合之后，即图5中（b）～（d）发生明显的拐点之后，SPH计算结果与实验结果相对符合度差了些，但总体趋势基本保持一致。主要是由于水-气相互作用导致的能量耗散考虑不足，在自由表面附近，液体间的碰撞融合过程伴随有黏性耗散作用，对自由表面的形成和自由表面的演化过程有重要影响，这是本文计算和实验产生差异的重要原因。

2.3 监测点压力变化比较

图6展示了右侧壁面不同高度处压力随时间的变化过程，其中（a）～（d）分别展示了距容器底部3，15，30，80 mm高处的SPH计算压力和100次传感器测试压力的95%置信区间的对比曲线，图中显示的压力为无量纲压力p，无量纲处理方式为实时压力与最大静水压力的比值，即p=p/（ρ0gH）。在3 mm处，压力几乎全部落入置信区间内部，其中在流体刚冲击到右侧壁面时，p*出现了最大值，且p=6.79，大于置信区间的最大压力值，这是因为流体与右侧壁面发生撞击，压力从0在极短时间内快速增加，压力梯度变化很大导致的。应用SPH方法研究文献[2]中的溃坝水流模型成果很多[5，8-11]，本文与文献[5]的结果做了对比，其中最大压力与文献[5]中的最大压力值相差不大。在水流与右侧壁面撞击，经过翻卷并倾覆，与主流区域相融合后压力也产生了波动，这主要是由于液体碰撞融合时，液面处于振荡状态，压力波向周围传递引起附近区域流体的压力产生振荡，这也是其余监测点产生压力波动的主要原因之一。

15，30 mm处的压力大部分落入置信区间之内，相比于文献[5]，大部分时间段的压力值大于置信区间的最大值，本文的部分计算结果略低于置信区间的最小值，但都比较接近于置信区间的最小值，这主要是固壁附近流体粒子受边界斥力和黏性力的共同作用后，固壁附近的流体粒子与壁面间的距离稍大于粒子间的初始间距，致使压力值偏小。

在80 mm处，几乎整个时间段域内的压力值均小于置信区间的最小值，流体经过翻卷并倾覆，与主流区域相融合后，压力开始升高，致使后半段时间内的压力均落于实验的置信区间之内，主要是因为加入了近似边界层理论，流体与壁面间产生了相应的黏性效应，使得流体与壁面的接触更加自然合理，从而使得后半部分的压力升高，更接近实验结果。

本文对不考虑层流边界层影响的条件也进行了数值计算，发现不考虑边界层效应时，压力波动较大，特别是在流体冲击壁面的瞬间，p*>10.0，在流体经过翻卷并倾覆后，流体的压力波动幅度和振荡时间都比考虑边界层效应大很多，这也证明了文中方法是有效可行的。另外文中近似边界层的厚度取为2.4mm，主要是从SPH边界计算方法的角度进行考虑的，具体值的大小是根据边界粒子的支持域半径来定的，以后的工作可以结合边界区域实时雷诺数的大小和自适应粒子分辨率技术，详细研究边界层厚度的选取对不同流动问题的影响。

3 结 论

本文在耦合动力边界的基础上，在壁面附近引入层流黏性来近似边界层理论，应用改进的边界处理方法对经典溃坝问题进行数值模拟，并与实验结果进行了对比研究，得到以下结论。

（1） 较完整地模拟到了水流与壁面相互作用而产生的水花飞溅 、融合 、水流反弹、自由表面变化以及近壁面处水流的剧烈变形等多种复杂的物理现象，其外部轮廓与实验非常吻合。

（2） 自由液面的高度在水流发生翻卷并倾覆与主流区域相融合之前相一致，在自由表面融合过程中，由于液面间的冲击能量耗散，会导致融合后的液面高度存在一些差异。

（3） 数值模拟的压力基本落在100次实验研究的95%置信区间之内，近似边界层理论在80 mm处的压力变化的预测更加准确。

参考文献：

[1] 李云，李君.溃坝模型试验研究综述[J].水科学进展，2009，20（2）：304-310.

[2] Lobovsky L，Botia-Vera E，Castellana F，et al.Experimental investigation of dynamic pressure loads during dam break[J].Journal of Fluids and Structures，2014（48）：407-434.

[3] Lee T，Zhou Z，Cao Y.Numerical simulations of hydraulic jumps in water sloshing and water impacting[J].Journal of Fluids Engineering，2002，124（1）：215-226.

[4] Buchner B.Green water on ship-type offshore structures[D].Delft：Delft University of Technology，2002.

[5] Cercos-Pita J L.AQUAgpusph，a new free 3D SPH solver accelerated with OpenCL[J].Computer Physics Communications，2015（192）：295-312.

[6] Nguyen V T，Park W G.A free surface flow solver for complex three‐dimensional water impact problems based on the VOF method[J].International Journal for Numerical Methods in Fluids，2016，82（1）：3-34.

[7] Mokrani C，Abadie S.Conditions for peak pressure stability in VOF simulations of dam break flow impact[J].Journal of Fluids and Structures，2016（62）：86-103.

[8] Sun P， Ming F， Zhang A. Numerical simulation of interactions between free surface and rigid body using a robust SPH method[J].Ocean Engineering，2015（98）：32-49.

[9] Aureli F，Dazzi S，Maranzoni A，et al.Experimental and numerical evaluation of the force due to the impact of a dam-break wave on a structure[J].Advances in Water Resources，2015（76）：29-42.

[10] Sun P，Ming F，Zhang A.Numerical simulation of interactions between free surface and rigid body using a robust SPH method[J].Ocean Engineering，2015（98）：32-49.

[11] Oger G，Marrone S，Le Touzé D，et al.SPH accuracy improvement through the combination of a quasi-Lagrangian shifting transport velocity and consistent ALE formalisms[J].Journal of Computational Physics，2016（313）：76-98.

[12] 彭榮强.应用等位函数法模拟溃坝流动[J].长江科学院院报，2008，25（2）：11-12.

[13] Violeau D，Rogers B D.Smoothed particle hydrodynamics （SPH） for free-surface flows： past， present and future[J].Journal of Hydraulic Research，2016，54（1）：1-26.

[14] Shadloo M S，Oger G，Le Touzé D.Smoothed particle hydrodynamics method for fluid flows，towards industrial applications：Motivations， current state， and challenges[J].Computers & Fluids，2016（136）：11-34.

[15] Liu G R，Liu M B.Smoothed particle hydrodynamics： a meshfree particle method[M].Newyork：World Scientific，2003.

[16] Liu M B，Liu G R.Smoothed particle hydrodynamics （SPH）：an overview and recent developments[J].Archives of Computational Methods in Engineering，2010，17（1）：25-76.

[17] Yue W，Lin C L，Patel V C.Numerical simulation of unsteady multidimensional free surface motions by level set method[J].International Journal for Numerical Methods in Fluids，2003，42（8）：853-884.

[18] Lv X，Zou Q，Zhao Y，et al.A novel coupled level set and volume of fluid method for sharp interface capturing on 3D tetrahedral grids[J].Journal of Computational Physics，2010，229（7）：2573-2604.

[19] Gingold R A，Monaghan J J.Smoothed particle hydrodynamics：theory and application to non-spherical stars[J].Monthly Notices of the Royal Astronomical Society，1977，181（3）：375-389.

[20] Monaghan J J.Smoothed particle hydrodynamics[J].Annual Review of Astronomy and Astrophysics，1992，30（1）：543-574.

[21] Shao J R，Li H Q，Liu G R，et al.An improved SPH method for modeling liquid sloshing dynamics[J].Computers & Structures，2012（100）：18-26.

[22] Macià F，Sánchez J M，Souto‐Iglesias A，et al.WCSPH viscosity diffusion processes in vortex flows[J].International Journal for Numerical Methods in Fluids，2012，69（3）：509-533.

[23] Colagrossi A，Antuono M，Le Touzé D.Theoretical considerations on the free-surface role in the smoothed-particle-hydrodynamics model[J].Physical Review E，2009，79（5）：056701.

[24] Monaghan J J，Gingold R A.Shock simulation by the particle method SPH[J].Journal of Computational Physics，1983，52（2）：374-389.

（編辑：胡旭东）