高中数学建模的设计与思考

叶根福

【摘  要】数学建模是应用数学知识解决实际问题的基本手段，也是推动数学发展的动力。作为高中数学六大核心素养之一，新课标已明确把数学建模列入高中数学课程。但如何使这一核心素养在课堂教学中落地，仍然是我们高中数学教师的短板。近日，笔者参加了杭州市优质课评比，课题为新课程标准附录中的一个案例——体重与脉搏，经过反复地备课、磨课和上课，收获颇多。本文尝试通过作者对这节课的设计、思考与研究，为高中数学建模的设计提供示例，从而起到抛砖引玉的作用。

【关键词】高中数学;建模设计;体重与脉搏

一、过程设计与意图分析

（一）发现问题，提出问题

教师：都说“数学来源于生活又应用于生活”，其中应用于生活是指利用数学知识解决生活中的实际问题，也就是我这节课的主题——数学建模：体重与脉搏。

教师：医学研究发现，动物的体重与脉搏存在着一定的关系。若能明确这个关系，则有助于更方便、更有效地认识人类心脏病的发生、发展规律和研究预防措施，所以研究动物的体重与脉搏的函数模型意义重大。那么如何建立两者之间的函数模型呢？

设计意图：给出所要研究问题的背景，让学生体会意识到建立体重与脉搏函数模型的必要性。

（二）选定对象，收集数据

教师：那么要建立体重与脉搏之间的函数模型，首先我们要做什么？

学生：收集一些动物的体重与脉搏的数据，用来加以研究。

教师：很好，这是数学建模非常重要的一个环节，收集的数据准确与否直接影响后面我们所建立的函数模型是否符合实际。只不过由于时间、空间与道具的限制，这一环节没能在本节课上进行，这是通过大量测量以及大数据分析得到的一组动物的体重与脉搏的数据：

鼠（25，670），大鼠（200，420），豚鼠（300，300），兔（2000，205），小狗（5000，120），大狗（30000，85），羊（50000，70），马（450000，38）。

设计意图：虽然课堂时间有限，还是要让学生理解数据收集这一环节的重要性，当然，如果条件允许，提前布置学生进行课前数据收集则效果更佳。

（三）直观呈现，散点作图

教师：得到这些数据后，我们要怎么处理？

学生：为了使两组数据能更加直观地呈现出来，可以在直角坐标系中描点，画出散点图。

教师：很好，请同学们动手试一试。

学生动手作图，教师巡视，从中挑选几位学生代表进行实物投影，并对所画散点图进行点评与指导。（学生作图过程中自然能体会到由于数据很大，此处作图比较困难，前几组数据横坐标的差异很难在图中体现出来，只能作出简图。）

设计意图：让学生经历散点作图的过程，体会散点图的作用。同时也为后面通过对数据处理简化模型做好铺垫。

（四）回顾旧知，选择模型

教师：根据散点图的走势，你会选择什么函数模型？请列举你熟悉的函数模型。

学生：一次函数，反比例函数，二次函数，指数函数，对数函数，幂函数等。

设计意图：让学生回顾熟悉的函数模型，利于模型选择。

（五）利用数据，求解模型

教师：初步观察散点图的走势，你会选择什么函数模型？

学生：反比例函数模型[fx=kx]。

教师：好，根据你选择的函数模型与测量数据，请同学们求出函数模型（每四人一个小组合作完成）。

学生1：我们组选了点（25，670），得到函数模型[f1x=16750x]。

学生2：我们组选了点（200，420），得到函数模型[f2x=84000x]。

学生3：我们组选了点（450000，38），得到函数模型[f3x=17100000x]。

……

（六）结合实际，检验模型

教师：如何检验你所求出的函数是否符合实际呢？

教师：统计学中有多种方法刻画，其中使我们高中生比较容易理解的是用该函数模型的残差平方和大小来刻画。设测量数据为（[xi]，[yi]）[i=1，2，3，……，n]，拟合函数为[y=fx]，残差平方和

[SSE=y1-fx12+y2-fx22+……+][yn-fxn2]。

教师利用几何画板软件给出新概念残差平方和的几何解释即图中的[n]条线段的平方和，并通过动画引导学生得出残差平方和（[SSE]）越小，函数模型拟合程度越好。

教师：请同学们计算你们小组得到的函数模型的残差平方和，并判断所得模型是否符合实际。

学生1：我们组得到的函数模型是[f1x=16750x]，残差平方和[SSE=238391.7]，故该模型不符合。

学生2：我们组得到的函数模型是[f2x=84000x]，残差平方和[SSE=7286573.6]，故该模型也不符合。

设计意图：通过计算残差平方和，让学生学会如何整体检验一个函数模型是否符合实际。

（七）深入探究，合理优化

教师：数学建模过程中，得到不符合实际的函数模型是很正常的，需要我们不断的尝试。那如何重新选择函数模型呢？

教师引导学生分析反比例函数模型[fx=kx]不符合是由于下降速度不符，而函数[fx=kx2]，[fx=kx3]等函数图像也有类似走势，从而引导学生重新选择模型时可设函数模型为[fx=kxa]。

教师：好，请同学们利用数据再次合作求出函数模型。（学生合作计算，教师巡视）

学生（部分过程教师引导）：我們组选择点（25，670），（450000，38），把点代入[y=fx=kxa（a>0）]得：[k25a=670k450000a=38]，两式相除得：18000[a=33519] ，故[a=log18000=33519≈0.2929，][k=1720.]0118，从而得到[y=fx=1720.0118x0.2929]。不难计算该模型的残差平方和[SSE=4513.7]。

教师：很好，这个模型的拟合程度比前面得到的模型好了很多，下面我们通过图像再次对比（此处图略）。

教师：如果利用微积分的知识，我们可以求出最佳的[a]和[k]，使得残差平方和[SSE]最小（即最小二乘法）。

教师利用统计软件spss演示模型[fx=kxa]的最优解求解过程，得到最优解[fx=1790.9x0.298]，并从软件中获取该模型的残差平方和。

设计意图：得到不符合实际的函数模型后，引导学生通过对解析式的结构分析，重新选择函数模型。

（八）利用模型，解决问题

教师：如何利用函数模型解决实际问题呢？

学生：根据动物体重可以估计该动物的脉搏。

教师：老师的体重为72千克，则可估计老师的脉搏为多少？

教师：进一步地通过对此问题的优化分析，可以将体重与脉搏的比例关系应用于现代医学，进而达到预防疾病的目的。

设计意图：通过实际问题的解决，使学生切身感受数学建模的意义。

（九）数据分析，简化模型

教师：刚才我们在画散点图的时候，因为数据很大，所以画起来很困难，那么我们是否可以对数据进行处理，达到大数化小数的目的呢？

教师引导学生分析如10，10[2]，10[3]，10[4]……等数只要确定它的指数即可得到原数，从而自然地引出取对数的思想。

教师：通过对体重与脉搏两组数据，我们可以得到两组新的数据，类似的，我们不难得到新的散点图。

学生：显然这两组数据之间的关系更加清楚，不难想到选择一次函数模型。

教师再次利用spss演示模型[fx=kx+b]的最优解求解过程，得到最优解[fx=-0.298x+7.489]， 从而得到ln[f=-0.298xlnw+7.489]，然后与学生一起小结得出两者本质是一样的，但通过数据处理更容易得到模型。

设计意图：通过对数据取对数，达到简化模型的目的，同时培养学生的数据分析的核心素养。

（十）课堂回眸，感悟分享

这节课我学会了……

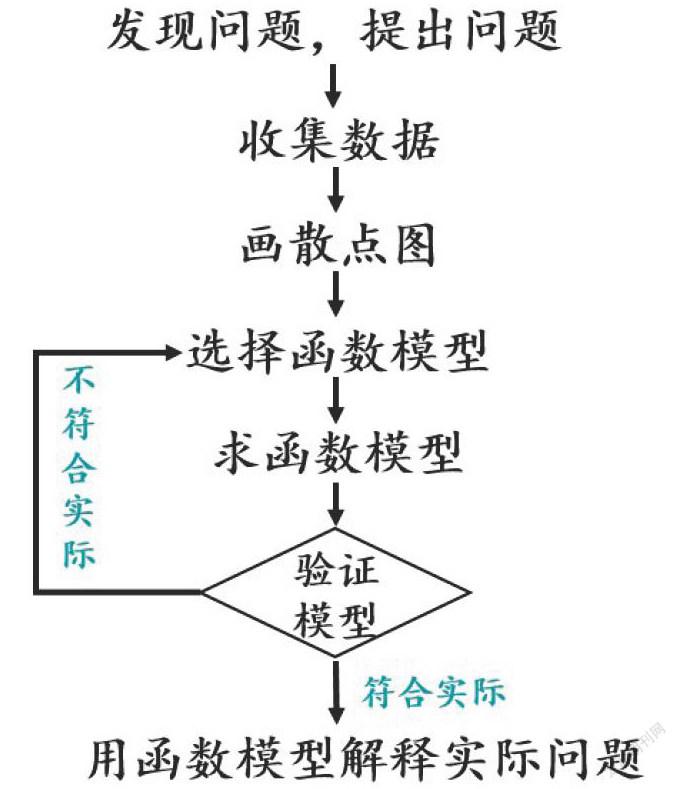
学生：建立函数模型的基本步骤：

教师：史宁中教授曾说：“数学学习的最终目标是让学习者会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界。”其中用数学的语言表达世界就是我们这节课的主题——数学建模。

设计意图：通过小结，使学生更加清楚建立两个变量函数模型的方法和步骤。首尾呼应，再次强调数学建模的重要性。

（十一）课后延伸，继续探究

1.小結整理建立函数模型的方法与步骤。

2.学习阅读材料，结合上课内容，写一篇数学建模活动的研究报告。

二、几点思考

本节课致力于发展学生的数学建模核心素养与数据分析核心素养。教师通过和学生一起经历体重与脉搏函数模型的建立，使学生学会建立生活中两个相关变量间函数模型的方法和步骤;通过函数模型建立的过程中的数据处理，使学生学会处理数据的基本方法。

苏霍姆林斯基说过：人的心灵深处都有一种根深蒂固的需要，就是希望自己是一个发现者、研究者、探索者。因此教师深入地研究学生已有的基础、可能存在的问题及应对策略至关重要，才能真正实现让学生在课堂上主动探究。

（一）要让学生感受建模的必要性

数学是自然的，是从实际生活中来的，收集数据并建立函数模型，能架起数学与现实生活的桥梁。本节课教师要让学生理解，建立体重与脉搏的函数模型对预防心脏疾病有重要意义，从而让学生感受建立该模型的必要性。

（二）要让学生经历建模的过程

授人以鱼不如授人以渔，教师只有让学生亲身经历建模、检验、重新选择模型、优化模型的过程，才能提高学生的建模素养与数据分析素养。本节课中反比例函数模型的选择与检验，幂函数模型的再次选择与检验，以及对数的数据处理方法等，都是让学生经历建模的过程，从而使两大素养的培养在课堂教学中落到实处。

（三）要让学体会模型的实用性

要想让学生真正对数学建模产生浓厚兴趣并不懈努力地提高自身的建模能力，教师就要让学生体会到利用模型能有效地解决现实世界中的实际问题，切身体会数学建模的重大作用。

参考文献：

[1]杨勇.用问题驱动探究，让结论自主建构[J].数学通报，2019（4）.

[2]吴菁.建模为桥——联结数学与生活[J].中国多媒体与网络教学学报，2019（5）.

（责任编辑  李 芳）