等腰三角形一题多解教学分析

陆俊兰

无论是在日常生活中还是在初中数学教学中，三角形的计算和运用是极为普遍的，而等腰三角形又是一种极其特殊的三角形，“一底二腰三条边，二角同架顶角尖;两腰等来两底等，计算运用想在先。”这就是对等腰三角形特殊元素及其性质的概括：即底边和腰（两腰相等），顶角和底角（两底角相等）。因为等腰三角形有顶角和底角之分，其边有腰和底之分，因而，在解决等腰三角形实际问题时，常常出现一题多解，学生也常常会忽视答案的另一种可能。根据本人十余年的教学经验，现将教学中最为常见的多解问题作如下简要分析。

一、等腰三角形一题多解问题的教学建议

1. 明确三角形的性质，等腰三角形属于普通三角形中特殊的一种，它具备普通三角形的所有性质。

2. 等腰三角形具有独特的性质，即两腰相等、两底角相等。

3. 特别提醒学生在解答等腰三角形问题时务必考虑多解因素，以免因疏忽而导致漏解。

4. 等腰三角形的无图题，即底和腰不明确、顶角和底角不明确、题目中等腰三角形的形状不明确时，更应提醒学生务必谨慎解题，充分考虑多解可能。

二、实例分类分析

1. 无图，腰与底不明确时， 则会造成多解。

實例分析：

（1）现有一块三角形空地，一边长6m，一边长9 m，若要把这块地砌墙围起来，请问围墙有多少？

错解：设底边的长是6 m，腰长是9 m。

则周长=6 m +9 m +9 m =24 m

分析：错解中判定底边的长是6 m，但是也可为9 m。当底边的长是9 m，腰长是6 m时. 周长=6 m +6 m +9 m =21 m

所以，此题为多解，正确答案应该是24 m或21 m.

（2）一等腰三角形的两边的长分别是5和12，那么这个等腰三角形的周长是多少？

错解：

设当底边的长是5，腰长是12时。

即周长=5+12+12=29

当底边的长是12，腰长是5时。

即周长=12+5+5=22

等腰三角形的周长是29或22.

分析：错解中判断此题为多解题，分别假设了底边、腰，从表面上看很全面，充分考虑了等腰三角形的多解性，但是三角形还具有一个性质：当底边的长是5，腰长是12时，5+5<12，偏离了“三角形任意两边之和大于第三边”的性质，不能组成三角形。

因此，此题的正确答案是唯一的，等腰三角形的周长是29。

2. 无图，当等腰三角形的顶角、底角不明确时，也会造成多解。

实例分析：

（1）如果等腰三角形的一个内角是另一个内角的4倍，那么这个等腰三角形三个内角的度数分别是多少度？

错解：

设顶角的度数为a，则底角的度数为4a。

根据根据等腰三角形的性质： a+4a+4a=180，解得a=20

所以，这个等腰三角形三个内角的度数分别是20º、80º、80º。

分析：此解题结果是不完善的，其判定底角是顶角的4倍是不全面的，没有底角一定大于顶角或顶角一定大于底角的说法。

应有另一假设：顶角是底角的4倍，即4a+a+a=180 º，a=30º，即可解得等腰三角形三个内角的度数分别是120º，30º，30º。

因此，正确答案是这个等腰三角形三个内角的度数分别是20º、80º、80º或120º、30º、30º。

一，由等腰三角形的高的不同。造成多解。

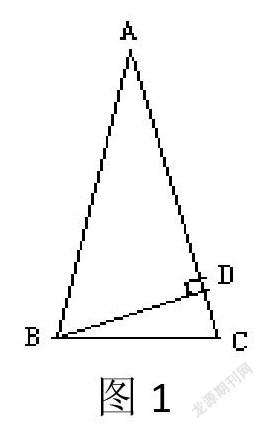
（1）在ΔABC中，AB=AC，BD是ΔABC的高，∠ABD=40º，求ΔABC三个内角的度数？

错解：如图1

由BD⊥AC， ∠ABD=40º，可知 ∠A=90º-40º=50º，

∴∠ABC=∠ACB=65º

∴这个等腰三角形三个内角的度数分别是50º、65 º、65 º。

解析：这个解法只考虑了等腰三角形的高在等腰三角形内的情况，而忽视了等腰三角形的高在等腰三角形外的情况。如图2，

当等腰三角形的高在等腰三角形外时，由BD⊥AC，

∠ABD=40º，可知 ∠BAC=90 º -40 º =50º

即∠BAC=180 º -50 º =130 º

所以，∠ABC=∠ACB=25º

因此，正确答案是这个等腰三角形三个内角的度数可能是是50º、65º、65º，也可能是130º、25º、25º。

总之，等腰三角形的教学应充分考虑其多解性，避免顾此失彼，题目简单而轻易出错。