随机车流作用下钢箱梁斜拉桥疲劳寿命评估分析
2019-09-10李少军孙一婵
李少军 孙一婵
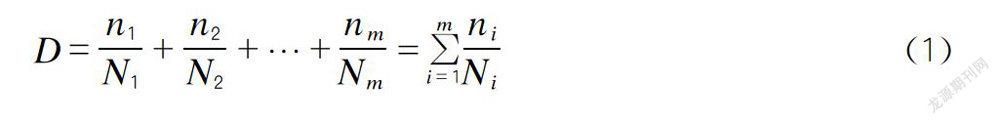



摘要:为了对大跨度钢箱梁斜拉桥在随机车流作用下的疲劳寿命进行评估,文章采用ANSYS有限元软件建立了东平河大桥跨中主梁标准节段壳单元有限元模型,通过计算分析得到了关键U肋位置的两种焊缝细节的应力影响面函数;参考某大桥动态称重系统的统计数据,建立了随机车流模型;通过数值模拟方法获取了钢箱梁细节的应力时程响应,对大桥关键位置焊缝细节的疲劳性能进行了研究,得出了一些有意义的结论。
关键词:桥梁工程;随机车流;应力时程;疲劳损伤;疲劳寿命
中图分类号:U448.213 文献标识码:A DOI:10.13282/j.cnki.wccst.2019.08.023
文章编号:1673-4874(2019)08-0084-05
0引言
随着我国经济的发展,城市交通量不断增加,导致大桥承受的交通荷载日益增长,然而大跨度钢桥在随机车流荷载的反复作用下,结构构件的应力随之循环变化并不断累积产生疲劳损伤破坏,将严重威胁大跨度钢桥的运营安全和使用寿命。因此合理评估大跨度钢桥结构及关键构件的疲劳性能成为桥梁结构全寿命周期性能评估的重要环节。
大跨度斜拉桥一般采用具有较好抗风性能的流线型扁平钢箱梁结构,其正交异性桥面板在车辆荷载的反复作用下容易产生疲劳损伤。随着运营时间的增长,疲劳损伤逐渐累积,在超过疲劳抗力后将会突然发生断裂破坏,甚至导致桥梁结构垮塌。因此,开展钢箱梁斜拉桥的疲劳寿命和疲劳可靠度评估具有重要的研究意义,本文基于数值模拟对东平河大桥开展了疲劳寿命评估的研究。
1疲劳寿命评估理论
由于车辆在桥面上行驶,桥面板通常受到变幅荷载的作用,为了确定常幅疲劳强度和变幅疲劳强度之间的关系,需要了解疲劳累积损伤理论。国内外有很多学者对这一问题进行了大量研究,在众多成果中,目前应用最为广泛的是PaImgren与Miner的研究成果。PaImgren-Miner线性损伤累积理论认为,变幅应力循环Si产生的疲劳损伤叠加构成总的疲劳损伤,计算式为:
式(1):ni为应力循环次数;Ni为S-N曲线中对应常幅应力幅值为Si的应力总循环次数。Miner准则中假定D≥1时,构件将发生疲劳破坏。
本文选取疲劳强度曲线时,参考的是欧洲EuroCode规范。由于疲劳损伤可以用等价原则进行处理,因此,可以用常幅应力循环来等效代替变幅应力循环,该常幅应力循环用Seq来表示。就公路钢桥的疲劳问题来说,低于应力截止限△σL的应力循环多于高于应力截止限△σL的应力循环,即在疲劳应力谱中,低应力循环占主要部分。因此计算变幅荷载作用下细节的疲劳损伤的公式可以改写为:
2工程背景
东平河大桥位于佛山市,为独塔双索面钢一混凝土混合梁斜拉桥,其中墩、塔和梁为固结体系,桥梁全长约408m,桥跨布置为64m+76m+268m,边中跨比为0.522;桥面以上塔高134.2m,塔高与主跨比约为1/2,边跨距主塔中心线75m处设一个辅助墩;主桥横桥向设双向2%横坡,桥面系宽36.5m,桥面布置为双向六车道。东平河大桥整体布置如图1所示。
3有限元建模及关键点应力响应面求解
为了实现荷载与应力效应之间的转化,计算车辆荷载作用下焊接点的应力效应基于ANSYS有限元软件平台,采用Shell63壳单元建立正交异性钢箱梁结构的有限元局部模型。结合正交异性桥面板局部荷载疲劳损伤特点,为了减少计算量,选用主跨跨中长度为18m的梁段,对其建立一半钢箱梁有限元模型,作为本章研究的计算对象,并对局部有限元模型的边界点的6个自由度进行限制。主梁的局部有限元模型与正交异性桥面板截面的横断面图如图2所示,选用的相应位置如图3所示。其中焊缝细节一为顶板一U型肋焊缝,焊缝细节二为U型肋对接焊缝,对应的焊缝细节编号分别为50和71,焊缝细节详细位置如图4所示。
确定关键点之后,沿主梁横断面方向选择三个行车道边缘,分别沿桥纵方向91个节点位置采用单位移动竖向力(1kN)依次进行加载,得到6个断面的各关键点疲劳参考应力的影响线竖标值,在此基础上利用MATLAB的数据拟合工具箱Curve Fitting TooIbox对该6条影响线进行线性插值拟合得到曲面,并将拟合得到的结果保存为可调用的函数形式。焊缝细节一与细节二的應力影响面函数如图5和图6所示。
从图可以看出,应力影响线的长度较短,主要集中在相邻的两横隔板之间,车辆荷载作用下桥面板的应力响应表现为极强的局部效应,由此验证了建立局部模型来分析桥面板焊缝细节疲劳性能的合理性。
4钢箱梁细节疲劳寿命评估
4.1车辆相关参数统计分析
由于东平河大桥还未开始通车,本文重点研究的是随机车流作用下桥面板的疲劳性能,因此,本文进行随机车流模拟时采用的车型占有率、车辆质量、车间距等概率统计参数参考相关文献中给出的参数,车速假设匀速。采用的日平均交通量为9800辆,分为六种车型,两轴小可客车划分为第一种车型,两轴卡车与大客车归为第二种车型,三轴、四轴、五轴和六轴货车依次为第三种、第四种、第五种和第六种车型,六种车型占比分别为0.58、0.11、0.03、0.04、0.06、0.18。由于本文建立的是局部模型,只需要考虑一个行车方向上的各车型在三个车道上的分布情况。车距通常情况下服从Weibull分布,其分布参数七为300,λ为10。
4.2随机车流样本生成
基于上述车型、车道、车距、轴重这几个相关车辆参数的分布类型与概率分布特性,在MATLAB平台,再按照各自对应的概率分布进行抽样得出随机车辆样本,连续抽样就可以得到在时域上的随机车流样本。在时域内生成随机车流的步骤如图7所示,图8为时长5min的随机车流样本。
从上述图示内容可比较明显地看出车辆的车型、车道、车重以及车距在桥面上随时间的变化,在时长为5min的通行时间内,通过车辆的数量在45辆左右。第六种车型在车型比例中占比较高且车重最大,因此,在钢桥面板的疲劳问题中,第六种车型应该引起重视。
4.3疲劳应力统计分析
基于拟合得到的标准梁段有限元模型的应力影响面函数与随机车流样本,可获取应力时程。本文生成了两个焊接细节在随机车流作用下的应力时程,每个细节的应力时程长度为5min,样本个数共计3万个。本文中由于标准梁段的应力影响面沿桥面行车方向的长度较短,当车辆的车轮位置超出该应力影响面范围时在影响面函数中数值记为零,且在标准梁段范围内各细节主要受拉力作用。
从图9(a)中可以发现,在时长为5min的随机车流作用下,细节一的应力变化范围大于细节二,其中细节一的应力范围基本在20MPa之内,细节二则一般<15MPa,总的来说,在同一时刻细节一的应力响应大于细节二,但两个细节的应力幅值均未超过常幅疲劳应力极限,可见,这两个细节的应力具有幅值低、频率高的特点。本文为了更加直观地研究随机车流作用下焊缝细节的疲劳损伤情况,对每一辆车的轴重进行了模拟,从图9(b)可知,应力响应较大时出现两个明显峰值,这主要是由多轴货车产生,多轴货车前后轴距较长,且通过桥梁某一截面用时比两轴车长,可形成多个应力峰值。
为了进一步分析各焊缝细节应力幅值与循环次数的变化情况,采用雨流计数方法对应力时程进行处理得到应力幅值与相应的循环次数。
从图10中可以看出,在两种构造细节中,低应力幅值的循环次数占绝大多数,高应力幅值的循环次数较少,但是低应力幅值产生的疲劳损伤非常有限,而高应力幅值产生的疲劳损伤占据主要部分,远大于低应力幅值所产生的。
4.4疲劳寿命评估
疲劳损伤一般按一天的时长来计算,由于本文采用的是时长为5min的应力时程样本,因此应将5min的循环次数换算为1d对应的循环次数,来计算1d大概的疲劳损伤,1d的循环次数计算公式如式(5)所示。焊接细节一与焊接细节二计算累积疲劳损伤的等效应力与循环次数如表1所示。
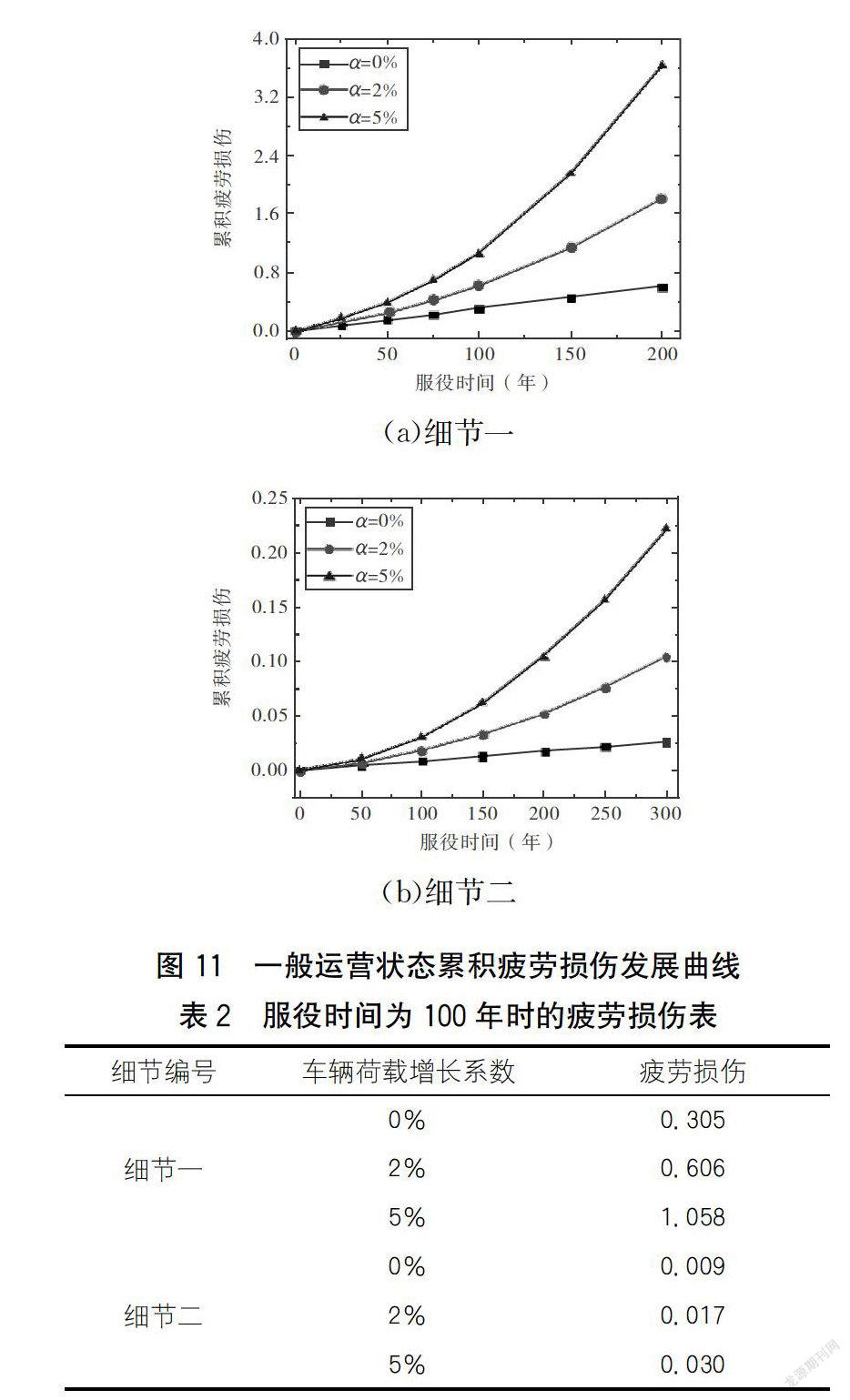
不考虑车辆荷载增长系数与考虑车辆荷载增长系数为2%和5%时,各焊缝细节不同年限对应的疲劳损伤如下页图11所示。
从图11中可以看出,不考虑交通量增长的情况时(车辆荷载增长系数为0%),累积疲劳损伤随着服役年限的增长呈线性增长的趋势,而当考虑交通量增长系数时(车辆荷载增长系数为2%或5%),随着服役年限的增长,累积疲劳损伤发展曲线呈非线性增长模式,并且随交通量增长系数的增加,累积疲劳损伤增长的速度越快。对比细节一与细节二可知,细节一达到累积疲劳损伤极限的服役年限比细节二的要短。表2为当服役时间为100年时细节一与细节二疲劳损伤的对比情况,从表中可知,当达到设计基准年限时,细节一的疲劳累积损伤将大于细节二的,因此细节一的安全问题更需引起重视,应定期安排检查与制定维修加固方案。
5结语
本文借助ANSYS有限元软件建立了东平河大桥跨中主梁标准节段的壳单元有限元模型,并运用MATLAB生成了随机车流作用下的焊接细节的应力时程,对桥面板U型肋两种焊缝细节进行了疲劳寿命评估。结果表明:
(1)在实测车流数据的基础上建立了随机车流模型,基于S-N曲线和线性累积损伤准则,给出了考虑运营状态和交通量增长的钢箱主梁标准节段顶板U型肋的疲劳可靠度研究方法。
(2)對比顶板-U型肋焊缝与U型肋对接焊缝,在各种运营状态下,顶板-U型肋焊缝达到累积疲劳损伤极限的服役年限比U型肋对接焊缝的要短。因此顶板-U型肋焊缝的安全问题更应该引起重视,定期安排检查与制定维修加固方案。
(3)结合正交异性桥面板局部荷载疲劳损伤特点,为了减少计算量,可采用主跨跨中长度为18m的梁段,且仅建立其一半钢箱梁有限元模型来作为疲劳寿命评估的研究对象。
