不因“简单”而“简略”在猜想验证中“一探究竟”
2019-09-10吴国明
吴国明
【摘要】《小数四则混合运算》是苏教版义务教育教科书五年级上册第五单元《小数乘法和除法》的第14课时。这部分内容是在学生学习整数四则混合运算和小数加、减、乘、除运算的基础上进行的,主要引导学生在具体的计算过程中,主动把整数四则混合运算的运算顺序及相关运算律推广到小数运算中。内容“简单”,但不意味这一教学程序可以“简略”,利用知识迁移的过程中,教师要重视引导学生进行合理猜想、探究验证,指导学生在猜想验证中“一探究竟”。
【关键词】《小数四则混合运算》;小学数学;猜想验证
一、案例片段
片段一:揭题提问,学生根据已有学习经验提出合理猜想。
师:我们已学习了小数的加、减、乘、除运算,我们今天将学习小数四则混合运算。(出示课题)看到这个课题你想知道些什么?
生1:小数四则混合运算怎么计算?
生2:小数四则混合运算和以前学习的整数四则混合运算有什么联系和区别?
师:不学习你们会计算吗?
生:会。
师:怎么计算?请用一句简单的话告诉老师。
生:我们猜测可以按整数四则混合运算的方法来计算。
师:非常好,同学们能联系已学过的内容进行合理猜想,那我们可以直接按猜想的方法来计算吗?为什么?
生:不可以,这样不科学,也不严谨。
师:那我们需要做什么?
生:我们还得验证。
师:很好,那我们的探究之旅就从帮助赵大伯解决实际问题开始吧。
片段二:探究小数四则混合运算的运算顺序。
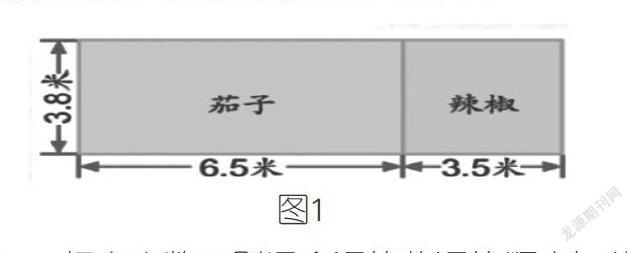
出示例题1:如图1所示,赵大伯在一块长方形菜地里种了茄子和辣椒。这块菜地的面积是多少平方米?
活动一:探究小数四则混合运算的运算顺序与整数是否相同。
活动要求:(1)根据题中信息可以怎样求这块菜地的面积?请列综合算式解答。(2)你是按怎样的顺序进行计算的?为什么可以这样计算?组内交流。(3)和整数四则混合运算的运算顺序比较,你们有什么发现?
生1:我是这样求的,茄子地的面积加辣椒地的面积等于菜地的总面积。列式为:6.5×3.8+3.5×3.8.6.5×3.8求的是茄子地的面积,3.5×3.8求的是辣椒地的面积,运算顺序是先算两个乘法,再算加法,结果是38平方米。
生2:这和整数混合四则运算的运算顺序是相同的,在既有加减法又有乘除法的算式里,应该先算乘除法,再算加减法。
生3:我是这样做的,(6.5+3.5)×3.8,先求出菜地的长,用菜地的长×宽=菜地的面积。所以计算时先算加法,再算乘法。这和整数混合运算的顺序也是一样的。
生4:我来总结一下。我们小组探究发现小数四则混合运算的运算顺序和整数相同。
片段三:探究整数的四则混合运算律是否适用于小数。
生:我还发现这两种解法是有聯系的,体现了乘法分配律。
师:哪里可以看出?
生1:因为6.5×3.8+3.5×3.8=(6.5+3.5)×3.8.
生2:我发现第二种方法更简便。
师:你们有什么想法?
生:我猜小数计算也能应用运算律进行简便计算。
师:仅以这一组算式能说明问题吗?
生3:不能,也许是巧合呢。
生4:那我们验证一下就可以了。
师:需要验证什么?怎么验证?
生4:验证所有的运算律,可以举例验证。
学生小组分工合作,举例验证。
二、案例反思
1.从学情出发,做合理猜想
美国著名的教育心理学家奥苏伯尔曾说:“假如让我把全部教育心理学仅仅归纳为一条原理的话,我将一言以蔽之:影响学习的最重要的因素是学生已经知道了什么,要探明这一点,并应就此进行教学。”小数四则混合运算对于学生来说非常简单,借助以往学过的整数四则混合运算的计算方法,学生很容易就会进行合情推理、合理猜想。片段一中,新课伊始,教师出示课题提出问题后,就问学生会不会计算,结果不出所料,所有学生都认为自己会算,认为“小数四则混合运算的运算顺序和整数相同”,且明确表示是他们猜测出来的。教师对学生能联系所学相近知识进行的合理猜想给予肯定,在学生感到得意时,让他们冷静思考:能否将猜想作为结论加以应用?这显然是不行的,学生认为这是“不科学”“不严谨”的,从而激发学生探究的欲望,突出验证猜想的必要性。学生自发地将学习活动推进到下一步,体现了学生学习是在教师的引导下自我建构、自我生成的过程,而非教师强行介入,学生被动执行。
教师以学生原有的知识和经验为教学活动的起点,尊重学生,从学生的学情出发,进行合理猜想,从而引领学生循序渐进地开展探究活动。
2.体验中发现,多角度验证
布鲁纳认为:“学习者在一定的问题情境中,对学习材料的亲身体验和发现的过程,才是学习者最有价值的东西。”片段二中,学生在对已有学习经验进行合情推理的基础上,借助解决赵大伯菜地面积的实际问题,学生用两种不同方法,根据解题思路、解题步骤理解算式的意义,确定计算的顺序,并和整数同类型计算的运算顺序进行比较,从运算顺序的一致性中验证了猜想,完成了对探究“活动一”的验证。
教师带领学生验证合情推理、合理猜想,得出结论,再加以应用。学生经历了“提出问题—合理猜想—设法验证—得出结论—加以应用”的学习过程,变被动接受为主动探索,这无疑会让学生在心理上产生一种极大的满足感和喜悦感,从而提高学习信心,激发学习兴趣,有利于学生学习能力的培养。
3.比较中发现,举例中验证
荷兰数学教育家弗赖登塔尔说:“真正的数学家,常常凭借数学的直觉思维做出各种猜想,然后加以证实。”片段三中,学生凭借已有的学习经验,感知两种解题方法之间的联系,发现乘法分配律的应用,且第二种方法更简便,从而引发新的猜想:运算律同样适用于小数计算,能让计算更简便。对于猜想是否成立,在讨论交流中学生认为需要全面举例验证,从而顺理成章地开展第二轮探究活动:小组分工,分别举例验证所学的5个运算律是否适用于小数的计算,并在合作交流中得出结论:运算律对于小数计算同样适用。学生合情推理、合理猜想,设法验证,学生在探究活动中一步步获得真知。直觉思维与逻辑思维的有机结合,不仅促进了学生思维水平的提升,而且培养了学生实事求是的科学态度。
对于小数四则混合运算的运算顺序及运算律的应用,两个看似“简单”的毫无难度的教学内容,却在这并不“简略”的学生猜想及自主探究活动中得以一步步验证。学生经历探究过程,验证猜想方法,有利于学生形成科学严谨的学习态度和综合数学素养。
【参考文献】
游建青.合理猜想,有效验证——运用“猜想验证”实施小学数学教学的有效探究[J].数学学习与研究,2016(22):167.
