探究数学课堂教学的设问

黄连旺

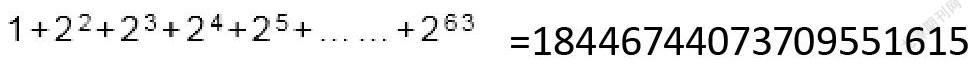
摘要：思维总是指向解决问题，教师在课堂上设计问题，不仅能巩固与检测教学效果，而且能促进学生把知识转化为技能，优化学生的思维和能力，所以，课堂教学中需要教师精心设计问题，优化学生的思维品质，提高学生的学习能力。

关键词：课堂;设问;思维;能力

课堂教学的设问，能增强学生的主动参与意识，增进师生交流，集中学生注意力，激发学生的学习兴趣，促进学生思维的发展，锻炼学生的表达能力。教师通过提问可以获取教学反馈信息，提高课堂的教学效果。在新课标下如何打造高效的数学课堂就成为教师面临的挑战。本文从以下几个方面谈谈自己的一些认识。

一、有效的課堂设问可以情境化，使其具有一定的趣味性，激发学生的学习兴趣。

合理有效的课堂提问在数学教学中能直接激发学生的学习兴趣，提高用数学思维和数学方法来分析和解决实际问题的能力，使学生由“学会”数学转变为“会学”数学。因此有效的课堂提问可以创设情境，让学生觉得数学来源于生活又用于生活，能够真正体现数学之奇，使枯燥的数学知识活跃起来，以激发学生的学习兴趣，引导学生主动参与数学学习。

例如，在教学“等比数列前n项和”时，教学情境可以引入“国王下棋的故事”：传说，古印度有一个人发明了一种游戏棋，棋盘共64格，玩起来十分新奇、有趣。国王要奖赏这种棋的发明者，问他想要什么，发明者说：“我只需要粮食，只要求在棋盘的第一个格子里放一颗麦粒，在第二个格子放两颗麦粒，第三个格子里放四颗麦粒……总之，后面格子里的麦粒都是它前一格的2倍，把64格都放满了就行。国王一听，满口答应。大臣们也都认为，这点麦粒，算得了什么，便领发明者去领麦粒。岂料，到后来把所有仓库里的存麦粒都付出了，还是不够。你知道这是为什么吗？

解：麦粒数根据制棋人的要求。可列式为：

=18446744073709551615

这些麦子究竟有多少？假定千粒麦子的质量为42克，据查世界年度小麦产量约6亿吨，请判断国王能否实现？引出学习等比数列求和公式的推导。这样一个情景的设立贴近生活，激发学生的好奇心，引导学生主动探索。

二、有效的课堂设问可以开拓启发学生的思维空间。

有效性的课堂提问不仅要能激发学生强烈的求知欲望，而且还能促使其知识内化，促进学生思维发展。通过问题的设置，引导学生多角度，多途径寻求解决问题的方法，开拓思维，培养思维的发散性和灵活性。通过教师的启发引导，学生去探索，充分发挥了学生的创造性思维。教师设置的提问还需问在学生有疑处，有疑问才会有争论，有争论才能辨别是非，也才能引起学生探求知识真理的兴趣，特别是经过教师的引导，同学之间的交流，使问题得到解决.例如，在教学《余弦定理》这节课时，学生已经学习了正弦定理，而本节课学习的内容与正弦定理有一定的联系。为此教师就利用这个旧知识，提出了这么一个问题：

（1）在△ABC中，已知a=15cm，b=10cm，A=60°，则c等于多少？

帮助学生复习正弦定理，学生解决了这么一个问题后，教师引导学生复习正弦定理的是如何推导出来的，为学生学习余弦定理铺设了桥梁。在此基础上，教师提出了第二个问题：

（2）在△ABC中，已知c=15cm，b=10cm，A=60°，则a等于多少？

通过解决这个问题，再引出了更加一般化的问题：在△ABC中，已知c，b，A，则a等于多少？，将学生引到本课要学习的余弦定理。

知识之间都存在联系，一节课的内容也不是孤立的。虽然一节课学习的内容是有限的，但是每节课的内容就形成了整个知识网络，他们之间存在着内在的联系。教学中，如果只立足一节课的内容，没有沟通知识的前后联系，就势必会影响到学生系统知识结构的建构。在新旧知识的链接点设置问题，能很好的解决这个问题，促进学生思维发展。

三、有效的课堂设问增强学生的主动参与意识，增进师生交流，集中学生注意力。

教学过程中的师生交流主要体现在一问一答中，巧妙、有效的“问”，能使交流反馈更加及时、顺畅;通过学生的“答”，能及时洞察学生的学习心理，及时调整教学策略;同时教师可以巧妙的利用每一次问答机会和学生进行情感交流，给学生以鼓励和帮助，融洽师生关系，创建和谐课堂。这样有效的课堂设问要有针对性和适度性，能调控整个教学过程。

例如，学习必修2《圆与圆的位置关系》这一节时做好以下的设问：

1.两圆的位置关系有哪些？注：初中学过，引起回忆。2.判断两圆的位置关系，有什么好的方法吗？注：好的办法是利用连心线的长与两圆半径和、差的关系发现判断和解决两圆的位置关系的方法…3.课本第129页例3中能根据题目，在同一个直角坐标系中画出两个方程所表示的圆吗？能从中发现了什么？4.根据你所画出的图形，可以直观判断两个圆的位置关系吗？5.从上面你所画出的图形，你能发现解决两个圆的位置的其它方法吗？6.如何判断两个圆的位置关系呢？阅读例3的两种解法，并加以归纳总结：一是判别式法，二是圆心距法。7.归纳总结：判断两个圆的位置关系方法？它们的特点是什么？

在学生合作交流中，答案马上出来了。所以通过问答，教师能及时了解学生的思维过程，避免教师想当然、误解学生，同时通过及时调整，让学生大胆发言，可以使学生建立学习的信心，并且在以后的学习中更加积极主动。

四、课堂设问可以通过创设数学实验情境，增强学生理解抽象的数学问题。

如排列组合知识作为高中的选修内容，由于抽象程度很高而成为“教”与“学”的难点。很多时候我们很难用清晰简洁的语言把题目讲清楚，且学生的认知水平也存在差异，从而思维能力受到了很大的限制，因此学生对题目的理解一知半解、模棱两可。

例如在讲解高中选修2-3的组合中的分组、分配问题时可选例题：

6本不同的书，按下列条件，各有多少种不同的分法：

（1）分成三份，一份1本，一份2本，一份3本;这是分组问题。

（2）分给甲、乙、丙3人，一人1本，一人2本，一人3本;这是上一问的基础上再分配。

在课堂上可以让一个学生拿出6本书进行分组实验：一份1本，一份2本，一份3本，可以让三个学生做分6本书实验：一人1本，一人2本，一人3本。

这里的关键就是将抽象问题具体化、生动化，让学生成为题目中的“演员”，成为问题解决的主角，从而提高学生学习的兴趣与积极性，同时还可以充分调动学生学习的积极性。

总之，设计问题时，还需要考虑设问的对象、提问时机等。归根结底，所谓数学课堂中有效设问，其实就是一切围绕学生为主体，发现、寻找使课堂教学有效开展的问题情景，在合适的时间、合适的空间以合适的方法把它呈现出来，让学生能迅速、正确地理解问题的指向，充分培养学生的思维能力，使不同的学生在数学能力上得到不同的、他所需要的发展。

参考文献：

[1]《数学教学通讯》2013年2月;

[2]《数学教学通讯》2012年9月;

[3]《高中数学教与学》2012年第一期。