农村初中数学教学中数形结合思想的实践分析

李海青

摘要：随着新课改进程更广泛更深入地推进，农村教育越来越受到国家的重视。由于农村的教学条件不够富裕，师资力量有限，在新课改背景下，农村的初中数学教学正面临着极大的挑战，同时也存在很大的发展机遇。若要提高农村初中数学教学质量，农村教师就需要改变教学方法，数形结合的思想方法就非常有利于学生学习数学。本文主要分析数形结合的数学思想在农村初中数学中的应用实践。

关键词：农村初中;数学教学;数形结合;实践分析

初中数学是为学生未来更高层次的数学学习打基础的关键阶段，初中数学知识较为抽象复杂，再加上初中生的抽象逻辑思维还处于经验型，理解纷繁复杂的数学知识具有一定的困难。数形结合的思想方法是把图形和数字结合起来，帮助学生直观感受抽象的数学概念和原理，有助于加深学生的理解记忆[1]。农村初中数学教学的特殊性，要求农村教师需要因地制宜，教给学更好的学习方法。因此，将数形结合思想应用在农村初中数学教学中，有助于突破农村教学环境的限制，让学生更好的学习数学知识。

一、在函数问题中运用数形结合思想

函数在整个初中数学学习过程中占有重要的位置，在中考试卷中也占有很高的分值，但是函数方面的问题比较抽象复杂，学生理解起来有一定的困难。不同的函数具有自己不同的图像和性质，函数与其图像是紧密联系在一起的，学生在解题过程中画出函数的图像，尤其是对于解决二次函数的问题来说，很多时候就能找到解决问题的突破点[2]。因此，农村教师在讲解函数的过程中，要让学生养成运用数形结合思想解题的习惯。

例如，讲授人教版初中数学九年级上册《二次函数y=ax2+bx+c的图象和性质》时，教师在教学过程中可以渗透数形结合的思想，给学生提供有关的数学问题，如这道数学题：已知二次函数y=x2-x+a（a>0），当自变量x取m时，其相应的函数值y小于0，那么下列结论中正确的是

（A）m-1的函数值小于0（B）m-1的函数值大于0

（C）m-1的函数值等于0（D）m-1的函数值与0的大小关系不确定

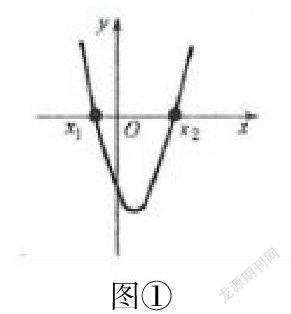
教师在讲解这道题时，要让学生从二次函数的图形入手，确定图像的大致位置，根据图像的特点来确定m-1的大小。让学生动手画出二次函数的草图，可以看出这个函数的开口向上，由已知条件“当自变量x取m时，其相应的函数值小于0”可以得出二次函数的图像与X轴有两个交点。二次函数的草图如图①所示：

设x1，x2是方程x2-x+a=0的两根，故x1+x2=1，x1*x2=a，|x1-x2|=√（x1+x2）2-4x1x2=√1-4a，因为a大于0，所以√1-4a小于1，所以|x1-x2|小于1，又因为当自变量x取m时，其相应的函数值y小于0，所以当自变量x取m-1时，m-1的函数值y大于0，故答案选B。类似的二次函数题都要借助函数的图形来求解，才能得出正确的答案。

二、在不等式问题中运用数形结合的思想

初中生在学习过程中，经常仿照老师运用的代数方法去解决同类问题，但学生并不能深刻理解所用方法的意义，如果转换出题的形式，学生就很难想到用同样的代数方法解题。如果在讲解不等式时，让学生明白题目的几何意义，那么无论出题形式怎么变化，学生都能抓住解题的关键。因此，农村教师在教学过程中要渗透数形结合的思想，帮助学生将题目快速解答出来。

例如，讲授人教版初中数学七年级下册《不等式与不等式组》这一单元，初中数学教材讲解的是一元一次不等式，涉及到的题目难度相对来说不大，很多都是如|x-2|<6这样的题目，教师在讲解时引导学生探寻他们的几何意义，由此入手培养学生运用数形结合思想来解题，把题目中给出的已知条件转换成数轴的问题，相当于是说x与2相距的距离小于6，这道题的答案就是划定范围中全部的有理数。如果只是单纯运用代数方法求解，会增加解题的步骤，降低学生答题的速度。通过培养学生数形结合的思想，将复杂的不等式题目与数轴结合起来，使学生能够从直观上分析所求的问题，有助于学生快速得出正确的答案。

三、在方程应用题中运用数形结合的思想

初中数学中涉及到许多应用问题，这是考试重点考察的内容，也是学生解决起来比较困难的一类问题。很多应用题给出的已知信息量比较大，学生理解起来有一定的困难，需要把题目重复看好几遍，非常耽误做题时间。因此，在解决应用题时，采用数形结合的思想方法，将繁多的数字文字信息变成直观的函数图象进行求解，不但节省了做题的时间，也提高了做题的正确率。

例如，讲授人教版初中数学七年级上册《实际问题与一元一次方程》，有一些应用题需要教师引导学生，采用数形结合的思想来解决，如解决相遇问题：A、B两地之间相距360千米，甲车从A地出发开往B地，速度为72千米/小时，乙车从B地出发开往A地，速度位48千米/小时，两车同时出发，多少小时候两车相遇？这种应用题如果只是单纯地靠大脑想象，解題速度就会很慢，如果学生在草稿纸上画出两车的线形示意图，就能把题目给出的信息简单直观的表达出来，从而快速找到题目中相等的数量关系是甲车行驶的路程+乙车行驶的路程=总路程，进而列出方程。设两车同时出发后x小时相遇，由题目可得72x+48x=360，x=3，所以两车出发后3小时相遇。这道问题还可以改成若甲车出发30分钟后乙车再出发，求乙车出发几小时后两车相遇？教师引导学生画出线形示意图，找出问题中的等量关系是甲车前30分钟的路程+甲车30分钟后的路程+乙车行驶的路程=总路程，设乙车出发x小时后两车相遇，由题目可得72*1/2+72*x+48x= 360，即可求得x=2.7。

结束语

初中数学较为抽象和复杂，为了让学生更好的理解抽象的数学知识，农村初中教师需要因地制宜，传授给学生数形结合的思想方法，将问题变得简单直观，使学生能够快速找到解题的突破口，提高做题的速度和正确率。

参考文献：

[1]谢良毅.数形结合思想在初中数学教学的运用[J].福建基础教育研究，2018（1）：79-81.

[2]张宏.提高农村中学数学教学效果的几点认识[J].学周刊，2017（30）：118-119.