图形联袂求极值 数理携手筑思维

张彦升　徐恒震　张丽萍

摘   要：针对三则富有代表性的连接体极值问题的案例进行剖析，并巧以图像法嵌入，以此将物理问题转化为函数关系，将物理过程转化为图像语言，由此实现问题解决与思维培植的双赢，进而获得学科素养之科学思维的提高。

关键词：高中物理;连接体极值问题;图像法

中图分类号：G633.7    文献标识码：A    文章编号：1009-010X（2019）32-0004-03

物理学中的连接体泛指两个（或两个以上）物体通过叠放、媒介（轻绳、轻杆、滑轮）等维系所构成的系统。连接体问题具有过程复杂、对象多元、综合抽象等特点，其中的连接体极值问题（也有称临界问题）是物体的运动状态发生突变的边界状态，其相应物理量的临界值（能量极值、速度极值、位移极值）是考查学生逻辑思维、发散思维的着力点。通过巧妙搭建a-t图、v-t图能将其化隐为显、化难为易、化冗为简，即使问题解决与思维培植同步共赢，现择三例进行阐释。

一、案例1：v-t图趣解能量极值

如图1所示，物块A、B通过弹簧相连，已知所有接触面光滑，弹簧起始处于自然伸长状态，两物块质量相等。现对物块A施加一水平向右的恒力F，物块A、B从静止开始向右运动，则下列说法中正确的是（   ）

A.弹簧第一次达到最长时，系统动能最大

B.弹簧第一次达到最长时，系统弹性势能最大

C.当A、B加速度相等时，系统的机械能最大

D.当A、B加速度相等时，两者的动能之差最大

【试题解析】A物体：F-kx=maA，B物体：kx=maB，随着弹簧伸长量x的增大，A做加速度减小的变加速运动，B做加速度增大的变加速运动，据此绘制图2。由图像可知：在t1时刻两者加速度相等，速度差最大，动能差最大;在t2时刻两者速度达到最大，系统动能最大，面积差最大，弹簧伸长量最大，弹性势能最大，则机械能也最大，故正确选项为ABD。

【思维解析】该题目源于2009年江苏卷第9

题的变形，体现了以下思维及特点：1.数形思维：v-t图能以斜率表征加速度的动态变化，同时使研究对象的运动过程更加清晰化、直观化，以数解形、以形助数，彰显了数形思维;2.模型思维：连接体本身是一种物理模型，在弹簧被拉长的过程中，当弹簧弹力与拉力大小相等时必然出现临界状态，产生极值问题，以模型为依托则能去粗取精，训练抽象思维;3.思维的灵活性：在解题中以隔离法明晰研究对象的加速度，由加速度推理速度，由速度推理位移，由位移推理能量，步步为营、节节推进，如此趣解物理问题，可体现思维的灵活性。

二、案例2：v-t图巧解位移极值

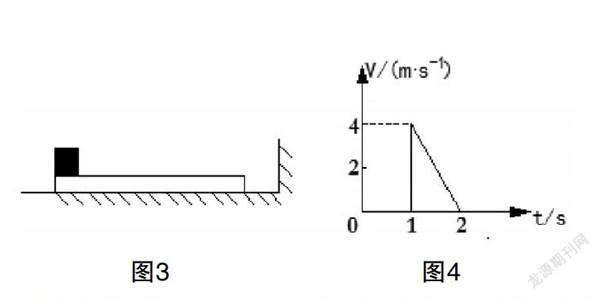
一长木板置于粗糙水平地面上，木板左端放置一小物块，在木板右方有一墙壁，木板右端与墙壁的距离为4.5m，如图3所示。t=0时刻开始，小物块与木板一起以共同速度向右运动，直至t=1s时木板与墙壁碰撞（碰撞时间极短）。碰撞前后木板速度大小不变，方向相反，运动过程中小物块始终未脱离木板。已知碰撞后1s时间内小物块的v-t图线如图4所示。已知滑板与地面、物块间的动摩擦因数分别为μ1=0.1，和μ2=0.4，木板的质量是小物块质量的15倍，重力加速度大小取10m/s2.求：

（1）木板的最小长度;（2）木板右端离墙壁的最终距离。

【试题解析】（1）规定向右为正方向。设经过t1，木板与物块具有共同速度v，碰后物块和木板加速度分别为a1、a2，速度为v1、-v1，物块相对于木板的位移为S1，由图4可知a1=-4m/s2，v1=4m/s.

由牛顿第二定律及运动学公式得：

μmg+μ（M+m）g=Ma

v=-v+at=v+at

解得：t=1.5s，v=-2m/s

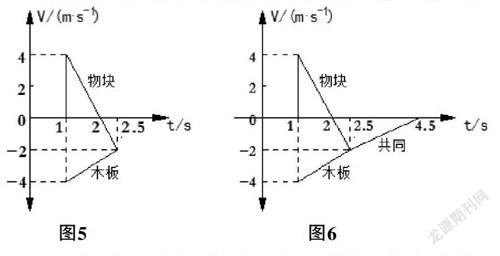
绘制图5，由图得：S=1.5m，S=4.5m（木板位移为负）

故物块相对于木板的位移S=S-S=6m

（2）物块和木板共速后向左做匀减速直线运动直至停止，设加速度为a3，用时为t2，木板右端离墙壁的最终距离为S2，由牛顿第二定律和运动学方程得：

μ（M+m）g=（M+m）a

v=at

解得：a=1m/s，t=2

绘制图6，由图知：物块与木板在t=4.5s时刻停止，则S=6.5m.

【思維解析】该题目源于2015年新课标Ⅰ卷第25题的变形，体现了以下思维及特点：1.逆向思维：物块与木板在2.5s～4.5s之间做匀减速直线运动，直接求解难以摆脱待求量过多的困境，辅助以逆向思维，则可将系统的匀减速直线运动反向视为初速度为零的匀加速直线运动，这体现了巧解物理问题，凸显正难则反、以反求正逆向思维的灵活性;2.整体思维：在物块与木板具有相同的加速度时，常将物块与木板视为一个系统，即不考虑系统内力，直接对系统运用整体法求解，这也是处理力学问题的基本思路之一;3.思维的深刻性：题干信息给出了碰撞后1s内物块的v-t图，碰撞前后木板速度大小不变，方向相反，这实际上是隐晦给出了木板运动的初速度，这告诉我们要善于抽离物理情境的复杂表象，挖掘隐藏信息，如此就能由此及彼、由表及里、化隐为显、化繁为简，展现思维的深刻性。

三、案例3：a-t图妙解速度极值

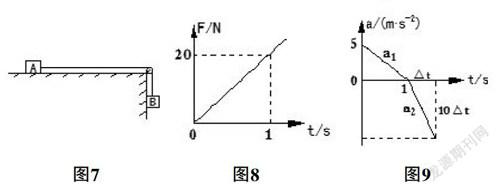
一平臺的局部如图7所示，水平面光滑，竖直面粗糙，动摩擦因数μ=0.5，右上角固定一定滑轮，一轻绳绕过定滑轮，轻绳左端系在一质量mA=1.0kg的物块A上，右端系住一相同质量的物块B，物块B刚好可与竖直面接触。起始时令两物块都处于静止状态，绳被拉直，设物块A距滑轮足够远，台面足够高，最大静摩擦力等于滑动摩擦力，忽略滑轮质量及其与绳之间的摩擦，已知未对物块B施加力F前，A、B共同加速运动的加速度为5m/s2，现同时由静止释放A、B，同时对物块B施加力F，方向水平向左，大小随时间变化如图所示，求物块B运动过程中的最大速度及施加力F后经多长时间停止运动？g取10m/s2.

【试题解析】当物块B受到水平向左的力F时，下滑时会受到竖直墙壁的摩擦力，以物块A、B为系统，由牛顿第二定律可得：

mBg-μF=（mA+mB）a

由F-t图可知：F=20t，化简得a=-5t+5，绘制图9 a1-t则物块B在t1=1s时，a=0，速度达到最大，vmax=×1×5m/s=2.5m/s

此后F继续增大，设物块B的加速度为a2，由牛顿第二定律可得：mBg-μF=mBa2

化简得a2=-10t+10，绘制图9a2-t

设物块B从vmax至停止运动所需的时间为△t，则只需两个三角形面积相等即×5×1=×△t×10△t，解得△t=s，故t=t1+△t≈1.7s.

【思维解析】该题目源于韩国2017年科学

探究领域（物理Ⅱ）第17题，体现了以下思维及特点：1.灵感思维：题目求解由牛顿第二定律和F-t的函数关系得到a-t的函数关系后，很多学生求解到这里很可能会卡住。实际上，巧以F-t图得a-t图，巧以加速度求速度，以图构图，另辟蹊径，妙解物理问题，这正是灵感思维的完美呈现;2.类比思维：由a-t函数关系求速度极值联想到常规的以v-t函数关系求位移极值，从联想到类比，搭建思维支架，实现触类旁通、一法多用，展现类比思维的巧妙之处;3.思维的敏捷性：题设物块B何时停止运动，巧以数形结合为思维抓手，可将题设转换为简单的数学问题（求三角形面积），如此可轻松实现极值问题的思维转换，凸显思维的敏捷性。

事实上，任何质量上乘的物理习题设置的初衷都并非局限于知识点的考查，它更隐藏着方法与能力，特别是思维能力的考查。嵌入图像求极值实际上就是一种思维转换，它将抽象复杂的物理过程转换为清晰明了的几何图像，将繁杂冗长的数学形式转换为具体简单的函数关系。“以理携数”突破了凝固型思维的“藩篱”，实现了化隐为显、化难为易、化冗为简，凸显了思维的灵活性、深刻性和敏捷性。现实中，“物理+”的深度融合是丰富教师外源性知识，形塑教师教学逻辑，激发更大红利的“金钥匙”，更是点亮学生发散思维，激活学生创新思维的“法宝”，因此要引起我们的重视以提高我们的教学质量。

参考文献：

[1]任佳蕾，张丽萍，李   炎.以实验撬动思维之探——“探究物体对电流的阻碍作用”教学纪实[J].物理教学，2018，（6）：47～48.

[2]张丽萍，董博清，李文娜.我国高中物理准教师外源性知识结构的现状与分析[J].课程·教材·教法，2009，（7）：90～92.

[3]董   静，于海波.教师个人教学逻辑：内涵、形成与发展[J].教育研究，2017，（10）：126～129.