用三个公式全面、完整地解决欧德斯猜想
2019-09-10李君池
李君池


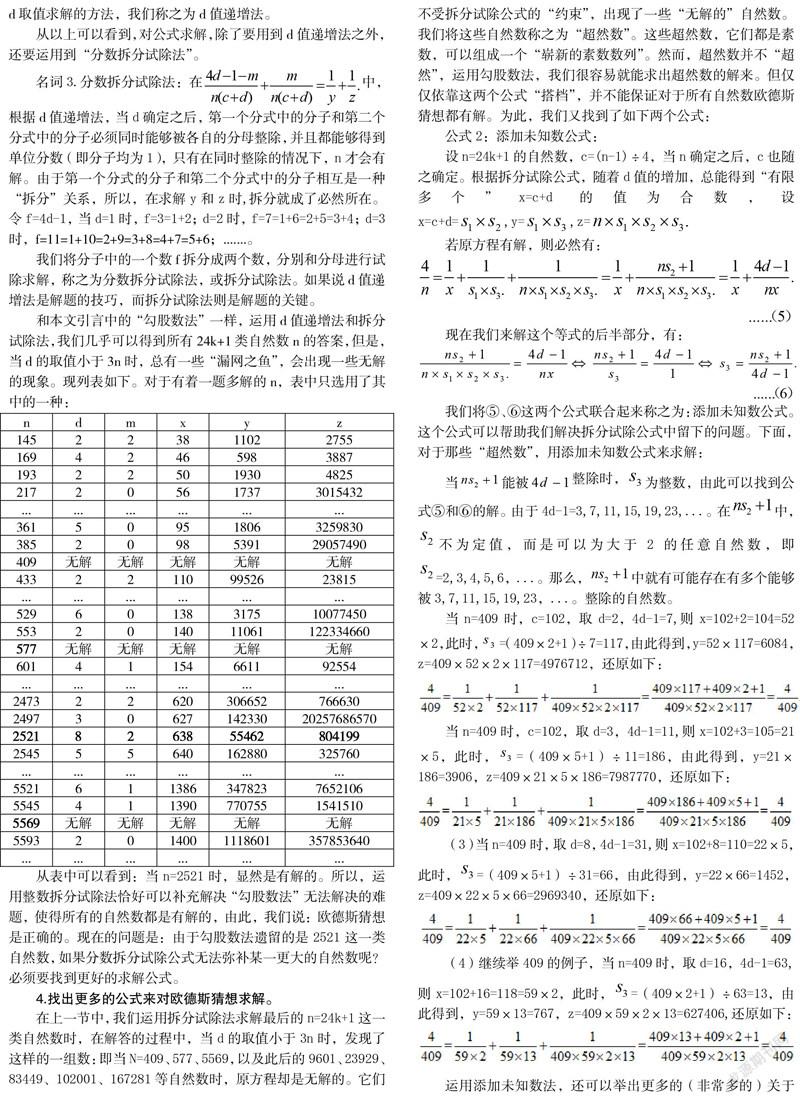

摘要:数学家保罗·埃德斯与恩斯特·斯特劳斯于1948年共同提出了一个数学猜想:对于所有n>1,方程4/n=1/x+1/y+1/z都有正整数解。自欧德斯猜想诞生以来,吸引了无数的数学家和数学爱好者进行了大量的探讨与研究,但七十年多过去了,一直没有什么大的进展,成了一道看似简单却又很棘手的世界难题。本文用三个公式全面、完整地解决了欧德斯猜想。文章的结论是:欧德斯猜想是一个正确的猜想。
关键词:欧德斯猜想;负余数;分数拆分试除公式;d值递增法;分数拆分试除法;超然数;添加未知数公式;递增综合公式;猜想正确
从表中可以看到:当n=2521时,显然是有解的。所以,运用整数拆分试除法恰好可以补充解决“勾股数法”无法解决的难题,使得所有的自然数都是有解的,由此,我们说:欧德斯猜想是正确的。现在的问题是:由于勾股数法遗留的是2521这一类自然数,如果分数拆分试除公式无法弥补某一更大的自然数呢?必须要找到更好的求解公式。
4.找出更多的公式来对欧德斯猜想求解。
在上一节中,我们运用拆分试除法求解最后的n=24k+1这一类自然数时,在解答的过程中,当d的取值小于3n时,发现了这样的一组数:即当N=409、577、5569,以及此后的9601、23929、83449、102001、167281等自然数时,原方程却是无解的。它們不受拆分试除公式的“约束”,出现了一些“无解的”自然数。我们将这些自然数称之为“超然数”。这些超然数,它们都是素数,可以组成一个“崭新的素数数列”。然而,超然数并不“超然”,运用勾股数法,我们很容易就能求出超然数的解来。但仅仅依靠这两个公式“搭档”,并不能保证对于所有自然数欧德斯猜想都有解。为此,我们又找到了如下两个公式:
运用此种方法解答欧德斯猜想,用人工计算,稍微麻烦一些,但用电脑解题,把公式输入就可以了。由于这种方法可以一个不漏地全面解决所有的自然数问题,因此,我们再也不用担心会出现“2521”、“超然数”等这一类难以解决的问题了。
5.结论。
本文根据负余数的理论,首先解决了自然数中欧德斯猜想的偶数问题,然后,对自然数中的奇数分开讨论,用多种方法一步步各个击破。当我们运用“分数拆分试除公式”,解决了“勾股数法”中遗留的2521这一类自然数时,却又产生了“超然数”这一新的问题。如果我们用“勾股数公式”回过头来解答超然数的问题,当然也是可以的。但仅仅依靠这两个公式搭档,并不能保证完整、全面地解决欧德斯猜想,还必须要找到更好的、可以完整地解答欧德斯猜想的公式。通过努力,我们又找到了“添加未知数”和“递增综合”这两个综合性的公式。特别是“递增综合公式”,它可以一个不拉地、全面地帮助我们解决欧德斯猜想中所有的自然数问题。至此,我们运用三个公式,全面、完整地解决了欧德斯猜想。
我们的结论是:欧德斯猜想是一个正确的猜想。
