采用石墨烯/聚二甲基硅氧烷的可调光栅设计及仿真计算
2019-09-10张周强王飞雷胥光申刘学婧曹亚斌闵渭兴
张周强,王飞雷,胥光申,刘学婧,曹亚斌,闵渭兴
(西安工程大学机电工程学院,710600,西安)
光栅作为一种重要的光学元件,被广泛应用于集成光路、光学测量、光通信、光信息处理等领域。可调光栅可通过外部激励(电激励、热激励等)来改变其周期,从而选择不同波长的光或将某一波长的光偏转不同的衍射角[1],相对于普通光栅来说是一种更具适应性和多功能性的光学元件。近年来,关于使用柔性材料制造可调光栅的研究越来越多,可调光栅以其结构简单、易于制造[2],以及能产生巨大应变[3]的特点受到了广大研究者的青睐。由于外部激励能促使可调光栅的周期产生快速变化[4],越来越多的柔性材料和刺激响应聚合物被用来制造反射光栅[4]和透射光栅[5]。Aschwanden等首次提出用柔性的电活性聚合物作为驱动器来控制衍射光栅的周期[1]。文献[6]提出了具有介电弹性体驱动器(DEA)的可调透射光栅,可用电压信号驱动光栅并调节光栅周期,但对驱动电压要求过高。当DEA材料为聚丙烯酸聚合物(VHB4910胶带)时,8.5%的周期调谐范围需要的驱动电压为3.25 kV;当DEA材料为热塑性弹性体(SEBS12)时,1.3%的周期调谐范围需要的驱动电压为2 kV。文献[7]提出了基于MEMS可调光栅器件的热驱动器,在该驱动器的作用下光栅间距的延伸率可达到25%,但其响应时间较慢、功耗较大。文献[8]提出了一种近红外光驱动的可调透射光栅,其中驱动部分为石墨烯/聚二甲基硅氧烷(GNP/PDMS)复合材料,光栅部分为PDMS材料,在近红外光驱动下光栅周期的调谐范围在3 s内可达到2.7%,具有响应速度快、功耗小等优点。
本文针对石墨烯具有优异的红外光吸收能力和良好的导热性能[9],并且GNP/PDMS复合材料具有在近红外光照射下响应十分迅速[10]等特点,以及氰化氢气体在1 528 nm波长附近存在不同强度吸收谱线的性质,设计了一种基于GNP/PDMS复合材料和PDMS材料的近红外光驱动的可调透射光栅,利用comsol软件分别对栅线沿驱动方向和垂直于驱动方向的光栅进行了数值模拟,并对仿真结果做了对比分析,可为后续关于可调光栅分光实验的研究提供理论指导。
1 光栅的结构设计
若衍射屏上周期性地分布着一系列透光狭缝,则可形成一种最简单的平面型透射式光栅[11]。光栅的结构如图1所示,相邻两狭缝的距离(即光栅周期)为d,透光部分的狭缝宽度为a,不透光部分的宽度为b,a+b=d。光栅也称为衍射光栅,是利用多缝衍射原理使光发生色散(分解为光谱)的光学元件。衍射光栅在屏幕上产生的光谱线位置可用光栅方程表示为
d(sinθ±sinα)=kλ,k=0,±1,±2,…
(1)
式中:θ为衍射角,即光的衍射方向与光栅平面法线之间的夹角;α为入射角,即光的入射方向与光栅平面法线之间的夹角;k为衍射级数;λ为入射光的波长。
由式(1)可知,当光的波长大于光栅周期时,不满足光栅方程,此时光栅的量程(可以测量的最大波长)为光栅周期。如果入射光的波长范围为(λmin,λmax),则经光栅衍射后,每一级光谱都有一定的空间分布范围,即角度分布范围。为了使光谱线不重叠,必须使第k级长波端λmax的谱线与第k+1级短波端λmin的谱线不重叠,即θmax(k)<θmin(k+1),又由光栅方程可得
λmax-λmin<λmin/k
(2)
入射光的波长范围必须满足式(2),才能保证第k级光谱不与k+1级光谱重叠,该波长范围称作自由光谱范围,即光栅可以自由工作的波长范围。

图1 光栅结构示意图
对于相同的衍射级数k,当入射角α相同时,衍射角θ随波长λ的改变而变化,但每一条衍射光谱都有一定的空间分布范围,如果波长间隔为Δλ的两条光谱线距离较近,则有可能相互重叠而无法分辨。根据光栅方程和多缝衍射公式推导计算可得,可分辨的波长间隔范围为
Δλ≥λ/kN
(3)
式中N为光栅狭缝的数量。
本文针对氰化氢气体进行了光栅的结构设计,查阅HITRAN数据库得到氰化氢在1 528 nm波长附近的吸收谱线如图2所示。由图可知,在1 519~1 534 nm的波长范围内,氰化氢存在不同强度的吸收谱线。当入射光垂直照射到光栅上,即α=0°时,光栅方程则为dsinθ=kλ。由于|sinθ|≤1,所以可得:当k=±1即一级光谱时,满足光栅方程的条件为d≥λ;当k=±2即二级光谱时,满足光栅方程的条件为d≥2λ。光路衍射时,为了同时产生一级和二级光谱,需d≥2λ,所以选取d=4 μm、a=2 μm、b=2 μm、深度为2 μm。由式(3)可知,N越大,光栅的分辨能力越强,对于氰化氢气体的检测,可选取N=1 500,即一级衍射的分辨率为1 500,可分辨的最小波长间隔约为1 nm。因此,可调光栅的结构参数确定如下:透明PDMS层的长度为4 μm×1 500=6 000 μm=6 mm,宽度选取为6 mm,两侧GNP/PDMS复合材料薄膜长度分别选取为20 mm,光栅厚度选取为0.1 mm。
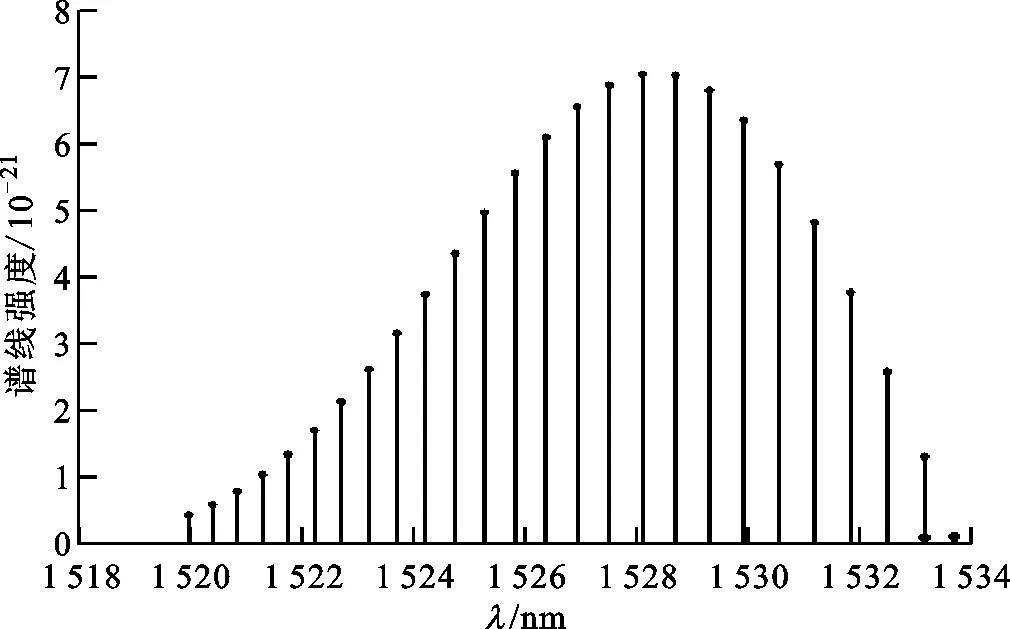
图2 氰化氢气体在近红外波段的吸收谱线
当GNP/PDMS复合材料中GNP的质量分数从0.1%增加到2%时,光引发的应力响应不断增强[10],且质量分数达到2%时,GNP/PDMS复合材料的光学机械响应趋于饱和。此时,在近红外光照射条件下,由于预应变的不同,复合材料薄膜会呈现出不同的变化状态:当预应变较低(<10%)时,薄膜膨胀,产生正应力;当预应变较高(>10%)时,薄膜收缩,产生负应力。膨胀变形和收缩变形均是可逆的变化过程,并且预应变达到40%时,光学机械响应达到最佳状态。本文设计的GNP与PDMS材料中GNP的质量分数选择为2%,并在近红外光照射前对整个光栅系统施加40%的预应变。在近红外光照射条件下,光栅两侧的GNP/PDMS复合材料薄膜产生可逆收缩变形,从而引起光栅中部的PDMS透明薄膜被拉伸,使得栅线沿驱动方向的光栅周期变小,垂直于驱动方向的光栅周期变大。当衍射光波长检测器的位置固定时,随着光栅周期的不断变化,接收到的波长也在不断变化,根据该波长与光栅周期的对应关系,即可选取所需范围的波长。
2 可调光栅的数值模拟方法
2.1 可调光栅模型
光驱动可调透射光栅的几何模型和结构参数如图3所示,其中:L1=6 mm;L2=20 mm;L=46 mm;W=6 mm;H=0.1 mm;a=2 μm;b=2 μm;d=4 μm;h=2 μm。

(a)栅线沿驱动方向的光栅结构
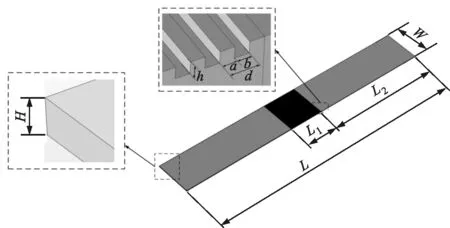
(b)栅线垂直于驱动方向的光栅结构图3 可调透射光栅的结构示意图
2.2 近红外光源模型分析
2.2.1 近红外光驱动光源 选择两个波长为808 nm的激光器作为驱动光源,分别垂直照射可调光栅两侧的GNP/PDMS复合材料薄膜部分并驱动光栅,驱动激光器与可调光栅的距离为50 mm,薄膜表面的功率密度为0.22 W·cm-2。
当使用近红外光驱动GNP/PDMS复合材料薄膜时,其光机械响应在5 s左右达到饱和[10]。对于两侧是GNP/PDMS复合材料薄膜的可调光栅,当驱动激光器工作3 s时,光栅周期的变化量达到最大值[8],因此本文将激光器的驱动时间设置为3 s,以模拟光栅周期达到最大值的变化过程。
2.2.2 近红外光驱动热源模型 在近红外光驱动条件下,石墨烯优异的光热转化能力使得GNP/PDMS薄膜温度迅速升高,产生的热应力将引起薄膜变形。在热输入分析中,热源的选择对模拟可调光栅中的温度场、应力场以及光栅周期的变化有至关重要的作用。
由于驱动激光器输出的激光热通量服从高斯函数分布,因此本文采用高斯分布热源模型进行仿真计算。高斯函数分布可表示为
QH=(2γP/πρ2)exp(-2r2/ρ2)
(4)
式中:γ为材料对光的吸收系数;P为激光器的输出功率;ρ为光束的有效半径;r为工作表面任意一点与光斑中心的距离。
2.2.3 PDMS材料与GNP/PDMS复合材料的属性 PDMS材料的热膨胀系数为9×10-4K-1,比定压热容为1 460 J/(kg·K),密度为970 kg/m3,导热系数为0.16 W/(m·K),杨氏模量为750 kPa,泊松比为0.49;GNP/PDMS复合材料的热膨胀系数为-3×10-4K-1,比定压热容为730 J/(kg·K),密度为960 kg/m3,导热系数为0.3 W/(m·K),杨氏模量为1 840 kPa[10],泊松比为0.48。
3 结果与分析
3.1 可调光栅栅线沿驱动方向的仿真分析
对图3a所示模型,采用comsol模拟了对其施加40%预应变后的相应变化。仿真结果表明,在施加预应变的方向,可调光栅总的长度(包括透明PDMS层和GNP/PDMS复合材料薄膜层)均比原长度增加了40%,宽度减小了1.25 mm,光栅周期由4 μm变为3.17 μm,减小了0.83 μm。
在上述仿真结果的基础上,模拟了该光栅在近红外光驱动条件下的响应。图4a所示为近红外光驱动条件下GNP/PDMS复合材料薄膜的温度分布图。使用3次多项式拟合了温度与时间的关系曲线,用决定系数R2表示函数的拟合优度(其值越接近于1,则方程的拟合程度越高),如图4b所示。拟合函数为
T=B0+B1t+B2t2+B3t3
(5)

(a)模型的温度分布

(b)光照位置的温度变化图4 栅线沿驱动方向时GNP/PDMS薄膜的温度变化
式中:t为时间;T为温度;B0、B1、B2、B3均为常数。由图4b可知,当使用波长为808 nm的近红外驱动激光器照射3 s时,GNP/PDMS复合材料薄膜的温度升高了大约55 ℃,最高温度达到75 ℃。
针对氰化氢气体的吸收峰(1 519~1 534 nm)进行了检测角度的设计,当光栅周期为3.17 μm时,波长为1 534 nm的光的一级衍射角约为28.94°。选择衍射角为28.9°的位置固定波长检测器用于检测波长的变化。图5给出了光栅不同位置处光栅周期与时间的关系,以及在28.9°检测角处波长与时间的关系。无论是光栅周期还是波长,其变化量与时间的关系曲线均可用多项式函数拟合如下
(6)
式中:时间t为自变量;光栅周期或波长的变化量Δd、Δλ为因变量;C1~C8均为常数。由图5可知,在近红外光驱动的条件下,光栅周期在光栅中部变化较大,两侧变化较小,调谐幅值约为21.3 nm,波长在该调谐范围内的最大变化量约为10.29 nm。图5中光栅周期的变化量均为负值,是因为激光器驱动可调光栅时,GNP/PDMS复合材料薄膜产生收缩变形,引起光栅部分被拉伸,从而使光栅周期减小所致。
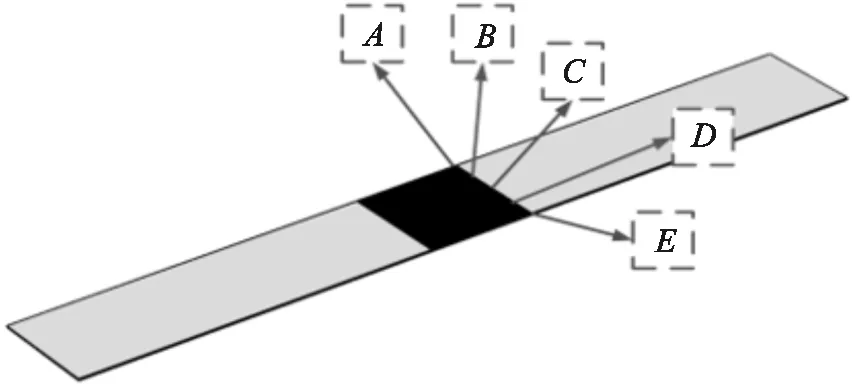
(a)柔性光栅模型
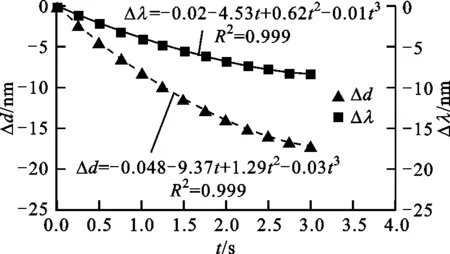
(b)位置A
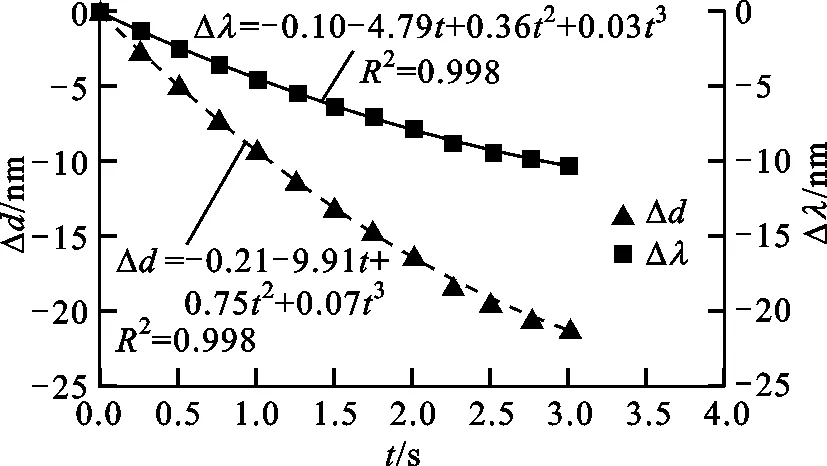
(c)位置B
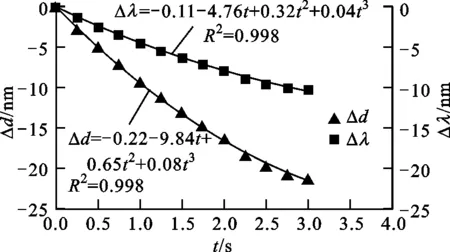
(d)位置C
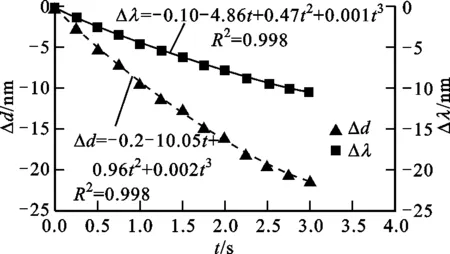
(e)位置D

(f)位置E图5 光栅周期/波长与时间的关系(栅线沿驱动方向)
可调光栅中部的光栅周期与波长的对应关系如图6所示,其中光栅周期由3 170 nm变为3 148.7 nm,检测角处的波长由1 532 nm变为1 521.7 nm。该波长范围满足吸收峰在1 528 nm附近的氰化氢气体的检测条件。

图6 光栅周期与波长的对应关系
3.2 可调光栅栅线垂直于驱动方向的仿真分析
对图3b所示模型,采用comsol模拟了对该光栅施加40%预应变后的相应变化,结果表明光栅周期由原来的4 μm变为5.6 μm。
在施加预应变的基础上,模拟了该光栅在近红外光驱动条件下的响应,GNP/PDMS复合材料薄膜的温度分布如图7a所示。使用式(5)拟合了温度与时间的关系曲线,如图7b所示。由图7b可知,当近红外激光器驱动3 s时,GNP/PDMS复合材料薄膜的温度升高了大约55 ℃,最高温度达到75 ℃。由于两种可调光栅(栅线沿驱动方向和垂直于驱动方向)的复合材料薄膜结构相同,并且近红外光驱动条件不变,所以温度仿真结果近似相同。

(a)模型的温度分布

(b)光照位置的温度变化图7 栅线垂直于驱动方向时GNP/PDMS薄膜的温度变化

(a)柔性光栅模型

(b)位置A
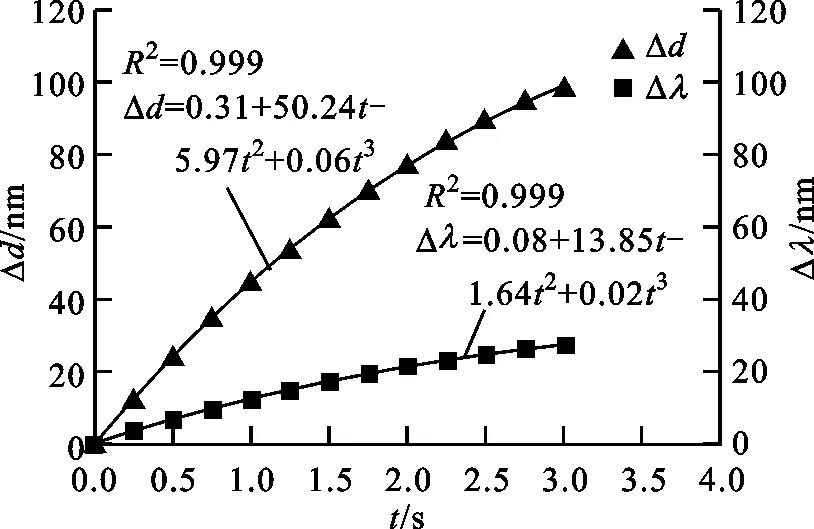
(c)位置B
(d)位置C
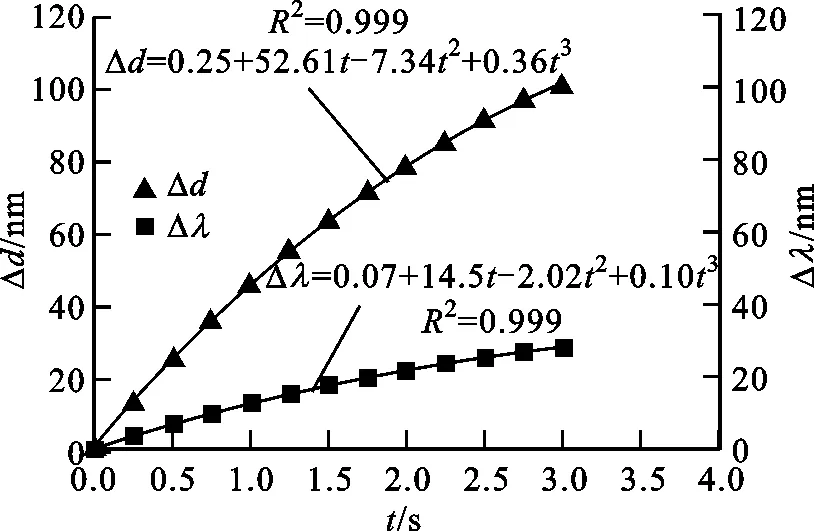
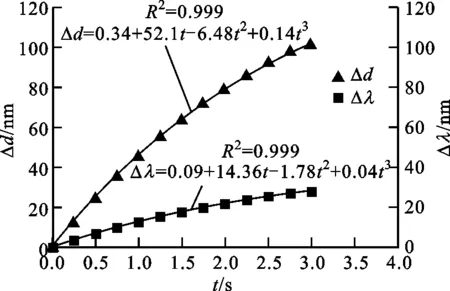
(e)位置D
当可调光栅的光栅周期变为5.6 μm时,波长为1 519 nm(氰化氢气体的吸收峰位于1 519~1 534 nm)的光的一级衍射角约为15.74°,所以检测角选择为15.7°。图8给出了近红外光驱动条件下光栅不同位置处光栅周期与时间的关系,以及在15.7°检测角位置处的波长与时间的关系。使用式(6)分别拟合了光栅周期与时间以及波长与时间的关系曲线,由拟合曲线可知,栅线垂直于驱动方向时,光栅中部的光栅周期的调谐幅值约为100.98 nm,波长在该调谐范围内的最大变化量约为27.33 nm,两侧的光栅周期的调谐幅值约为140.48 nm,波长最大变化量约为38.01 nm。
光栅周期与波长的对应关系如图9所示,其中光栅周期由5 600 nm变为5 700.98 nm,检测位置处的波长由1 515.36 nm变为1 542.69 nm,满足氰化氢气体的检测条件。
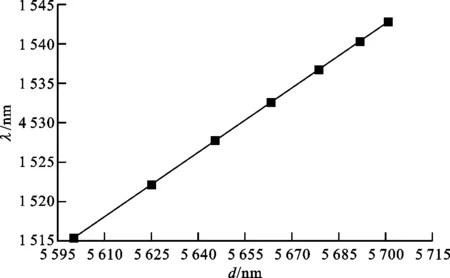
图9 光栅周期与波长的对应关系
3.3 结果对比分析
使用comsol模拟了近红外光驱动可调光栅对光栅周期的影响,发现当栅线方向与驱动方向一致时,光栅周期在光栅的中部变化较大,两侧变化较小。光栅周期的最大调谐范围位于光栅中部,幅值约为21.3 nm,波长在该调谐范围内的最大变化量约为10.29 nm。当栅线垂直于驱动方向时,光栅周期在光栅的中部变化较小,两侧的变化明显增大,但中间各部分光栅周期的变化趋于稳定,调谐幅值约为100.98 nm,波长在该调谐范围内的最大变化量约为27.33 nm。
鉴于上述光栅周期的不同变化方式,本文从微观角度切入,对位于光栅不同位置上的栅线变化进行了分析。栅线沿驱动方向的光栅周期变化如图10a所示,栅线垂直于驱动方向的光栅周期变化如图10b所示。结果表明,位于光栅中部的栅距变化均相对稳定,但两侧都会产生一定的突变,该突变对分光效果有极大的影响。光栅的有效分光区域为中间部分,如图10a所示光栅的有效分光区域距离光栅边缘0.63 mm,图10b所示光栅的有效分光区域距离光栅边缘1.2 mm。因此,使用柔性光栅进行空间调制时应控制光斑的大小和入射位置,使其照射于有效区域内。

(a)栅线沿驱动方向

(b)栅线垂直于驱动方向图10 光栅不同位置处光栅周期的变化量
为了验证上述数值模拟的可靠性,本文将近红外光驱动条件下可调光栅的数值模拟结果(复合材料薄膜温度变化与光栅周期变化)与文献[8]中的实验结果进行了对比,如图11所示。由图可知,无论是薄膜的温度还是光栅周期的变化量,模拟的变化趋势均与实验结果一致,但仍存在一定的差异,其中温度与光栅周期的变化量均服从线性关系,温度灵敏度约为1.73 nm/ ℃。造成该差异的原因主要是在进行GNP/PDMS复合材料薄膜制备加工时,受外界环境、加工工艺、材料配比等因素的影响,其属性值(热膨胀系数、泊松比、杨氏模量等)产生了一定的差异,而该差异直接影响了数值模拟的结果。

(a)温度变化对比
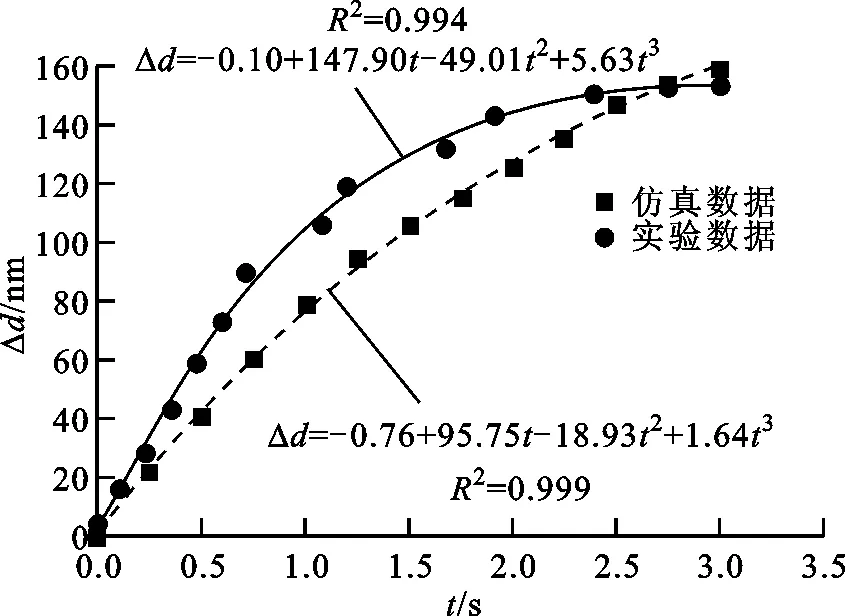
(b)光栅周期变化量对比
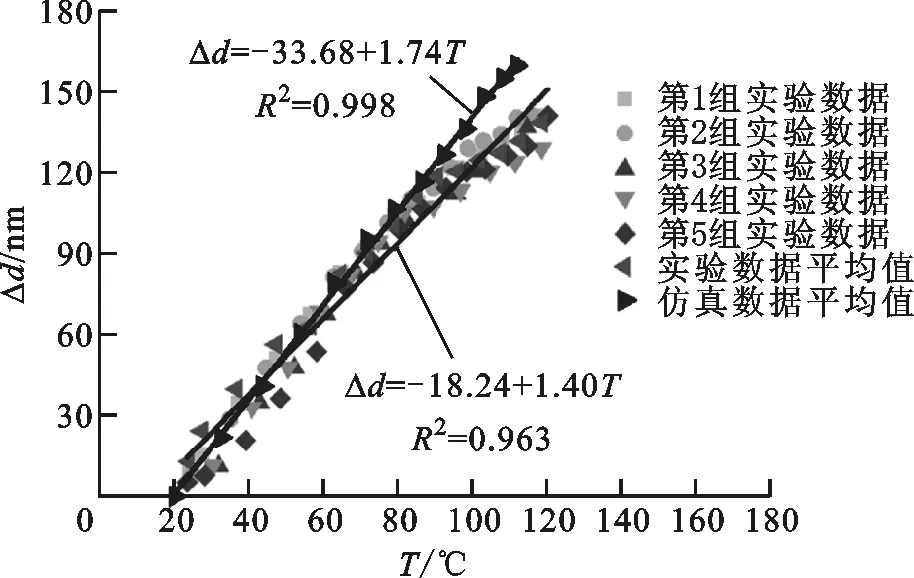
(c)温度与光栅周期变化量的关系图11 可调光栅的数值模拟与文献[8]实验结果的对比
4 结 论
本文针对氰化氢气体设计了近红外光驱动的可调透射光栅,重点研究了近红外光在不同方向(栅线沿驱动方向与垂直于驱动方向)驱动可调光栅对光栅周期的影响,揭示了位于光栅不同位置处光栅周期的变化规律,以及光栅周期与波长的对应变化关系,得出主要结论如下。
(1)当栅线方向与驱动方向一致时,光栅周期随着驱动时间的增加而减小,且在光栅中部的变化幅度高于两侧,变化范围为3 170~3 148.7 nm,对应的波长变化范围为1 532~1 521.7 nm。
(2)当栅线垂直于驱动方向时,光栅周期随驱动时间的增加而增大,且光栅中部的变化幅度低于两侧,变化范围为5 600~5 700.98 nm,对应的波长变化范围为1 515.36~1 542.69 nm。
(3)两种方式均能满足对氰化氢气体的检测,但值得注意的是,光栅两侧的光栅周期均会产生突变,故在进行分光时应控制光斑的大小与照射位置。该研究对后续氰化氢气体检测系统中的分光处理具有指导意义。
