基于隧道轴线控制的通用型管片主要构造参数设定研究

刘 欣

(广州地铁设计研究院股份有限公司， 广东 广州 510010)

0 引言

盾构法以其高效、安全、经济等优势，在市政道路、轨道交通、综合管廊、水利工程等领域得到广泛应用。随着我国经济高速发展，大型基础设施工程的建设力度空前，地下空间大力度开发，可利用的地下空间资源越来越少，隧道工程建设的边界条件越来越复杂，隧道小曲线半径转弯、大坡度线路敷设等情况屡见不鲜，因此对盾构隧道管片构造设计提出了更高的要求。为适应复杂工程建设条件下盾构隧道管片构造设计的要求，研究盾构管片的外径、环宽、纵向螺栓孔数以及管片楔形量等几何参数对盾构隧道的最小拼装半径以及拼装精度的影响是十分必要的。

目前，国内学者针对管片排版计算及纠偏方法开展了大量研究。刘凤华[1]、张志华等[2]通过分析盾构管片与设计线路的几何关系，各自提出了通用环管片的排版计算公式。张忠桢等[3]、刘欣等[4]则针对转弯环管片，分别利用齐次变换方法和几何迭代法对管片排版的位置和点位公式进行了推导。储柯钧[5]根据管片楔形量大小计算了在平、纵断面上的曲线纠偏时标准环与楔形环的配比。宗言海[6]、潘国荣等[7]分析设计线路的曲线要素特点及管片构造的几何特点，提出了通用环或者转弯环管片的纠偏计算方法。吴海彬等[8]基于通用楔形管片盾构隧道曲线段线路拟合原理、算法及相关规范，分析了不同管片参数对曲线拟合精度的影响。上述文献针对管片排版及纠偏已有较深入的研究，然而在实际工程设计过程中，在施工图开展之前，管片选型和构造设计往往已经确定，较少文献考虑管片构造的几何参数与设计线路的适应关系，且尚无针对此问题进行深入研究的案例。本文将以通用环双面楔管片为例，详细分析管片构造的各几何参数与隧道最小拼装曲线半径的关系，提出满足线路曲线半径拼装要求的管片几何参数组合，并基于实际工程中的设计线路，比较不同管片楔形量对拼装误差的影响，以期为实际工程的管片选型及构造设计提供合理建议。

1 通用环拼装设计基本思路

在刘欣等[4]提出的标准环+转弯环管片的排版计算方法的基础上进行扩展，可应用于双面楔的通用环管片拼装计算。假设盾构管片外径为D，环宽为B，楔形量为Δ。

本文未考虑盾尾间隙、管片环间张开量、错台等随机量的影响，是在理论上讨论管片几何参数与管片拟合能力的关系。如图1所示，针对盾构管片的几何特征和已完成拼装的管片数据分析，可得出如下管片几何变量和设计线路变量的定义：

1)tanα=Δ/(2D)；

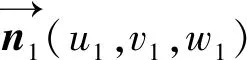
3)封顶块与管片拼装面水平左端点(9点方向)的夹角θ0；

4)当前线路方程f(L)及里程L0。

将盾构管片沿线路方向纵向投影，如图1(a)所示。设当前环终点面的最大楔形量短边角点为O4，可根据管片几何参数求解出当前环O4坐标(xo4,yo4,zo4)。

线段OO4长度与楔形量Δ关系为：

(1)

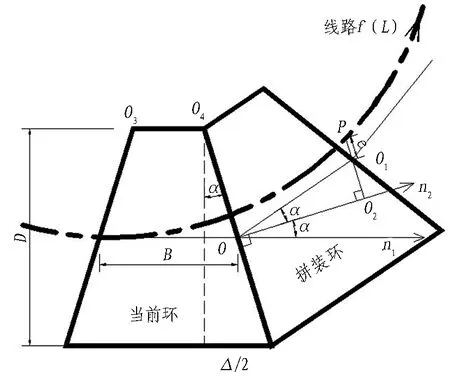
(a) 管片拼装姿态示意图

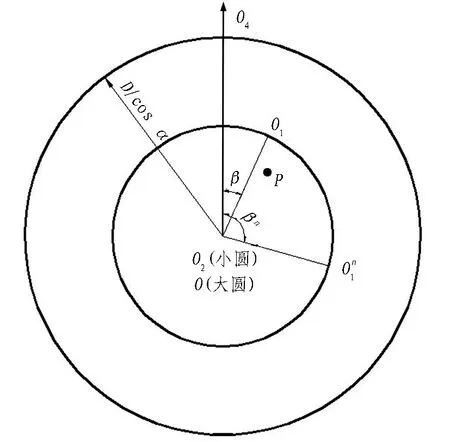
(b) 管片拼装点位旋转示意图

Fig. 1 Sketches of segment assembling posture and assembling point rotation

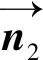
(2)

(3)

(4)

根据向量数量积公式，设拼装环终点面中心O1坐标为(xo1,yo1,zo1)，得出如下关系式：

(yo4-yo)(yo1-yo2)+(zo4-zo)(zo1-zo2)]/(Δ·B) 。

(5)

线段O1O4的长度由几何关系得：

(6)

线段OO1的长度为管片环宽B，得到：

(7)

联立式(5)、(6)、(7)，可求得拼装环相对当前环旋转β角度后的O1坐标 (xo1,yo1,zo1)。

通用环管片若采用错缝拼装方式，可根据管片分块构造及纵向螺栓组分布排除通缝拼装点位(对应的相对转角βx列为无效转角)，在求解上述方程时只计算能形成错缝拼装的有效相对转角值β(设存在m个有效相对转角)，每个β值对应有一组O1坐标解。

(8)

点P位于线路上，里程位于L=L0+B附近，将点P(xp,yp,zp)代入线路方程f(L|P(xp,yp,zp))，联立式(8)，迭代可求出点P坐标。

(9)

(10)

计算出拼装环最佳点位后，拼装环封顶块与管片拼装面水平左端点的夹角为θ1=θ0+β(若θ1>360°，θ1=θ1-360°)。在确定了拼装环的姿态后，下一环的拼装计算把拼装环作为当前环，重复上文内容，求解下一环的O1坐标，即下一环的管片拼装姿态。

2 管片几何构造对最小拼装半径的影响分析

盾构管片的外径、环宽、纵向螺栓孔数以及管片楔形量等几何参数限制着线路方案设计，影响着管片在线路曲线段的最小拼装半径和拼装精度。

1)管片内、外径的大小是对沿线地质情况、隧道深度、施工水平和运营限界条件等因素综合研究后决定的。由于施工技术的进步和隧道内部空间需求的增加，近年来大直径盾构隧道进入了大规模建设时期。管片直径的增大，将会制约线路设计的灵活性。

2)管片环宽的确定需要考虑盾构的构造、施工进度、施工水平及配套机械[9]。过大的环宽除了会削弱管片对线路的拟合能力，还会导致管片分块质量增加、盾构盾体加长、施工运输成本增加。过小的环宽会使隧道接缝增多、整体性变差、环缝渗水风险增加。

3)楔形量是管片能够进行曲线拼装的一个重要几何参数。小楔形量管片对线路的拟合能力和纠偏能力有限。大楔形量管片容易发生螺栓错位安装，隧道断面椭圆度增大，甚至出现拼装环突破盾尾间隙而造成管片卡壳事故。

4)环间纵向螺栓孔数量和管片分块情况决定了管片有效拼装点位数量，对成型隧道的线路精度有一定影响。

本文以通用环双面楔管片为例进行分析，其他类型的圆形管片与设计线路具有相同的几何关系。设通用环双面楔管片的内切楔形量位于封顶块中点，即封顶块中点为环宽最窄处。在小曲线拼装时，线路半径为R，管片状态如图2所示，管片①封顶块处于拱腰处，平面内楔形量最大。由于采用错缝拼装，先排除通缝拼装点位，定义备选拼装点位，假设沿管片周向均匀分布N组拼装点位，单位轴转角γ=360°/N。管片②不可与①点位相同，故管片②相对管片①发生一个单位轴转角γ时，隧道管片处于最小拼装半径的状态。

图2 管片沿曲线线路拼装示意图

将图2中线段fgh近似看作一段圆弧。扇形fah与扇形bac共用圆心a，根据相似原理，可推出如下等式：

(11)

式中C=2/(1+cosγ)，与有效拼装点位有关，一般有效拼装点位为8～12组，γ为30°～45°，则C∈[1.072, 1.172]。

由式(11)可知，在其他几何参数一定时，管片的线路最小拼装半径R与管片外径D、环宽B成正比，与楔形量Δ成反比。

楔形量、管片外径、环宽与管片最小拼装半径的关系见图3和图4。由图3可知，在管片外径为6 m、有效拼装点位为12组的条件下，环宽分别为1.2 m、1.5 m和2.0 m的管片楔形量与最小拼装半径的曲线变化趋势相似，在楔形量较小时，Δ-R下降曲线斜率大，楔形量变化对最小半径的影响明显。随着楔形量增大，Δ-R曲线趋于平缓，此时楔形量对最小拼装半径的改善效果不明显。图4描述了在楔形量、有效拼装点位相同(Δ=40 mm，拼装点位为12组)时，最小拼装半径与管片外径的关系。图4中，最小拼装半径随管片外径的增大呈线性增加，且较大的管片环宽Δ-D曲线的斜率较大。由式(11)也可看出，不同的环宽B1、B2在管片外径一定的情况下，最小拼装半径始终保持RB1=B1/B2·RB2的关系。

图5为有效拼装点位与最小拼装曲线半径的点位关系图。由图5可知，有效拼装点位小于8组时，对最小拼装半径的影响较大。在实际工程中，拼装点位一般大于8组，此时拼装点位对最小半径的影响较小，8～18组拼装点位的最小半径变化幅度在8%左右。因此，通过管片分块和纵向螺栓数量确定有效拼装点位时，应着重考虑隧道的整体连接刚度及材料和运维成本，螺栓数量增多对管片在最小拼装半径方面的拟合能力并无太大提高。

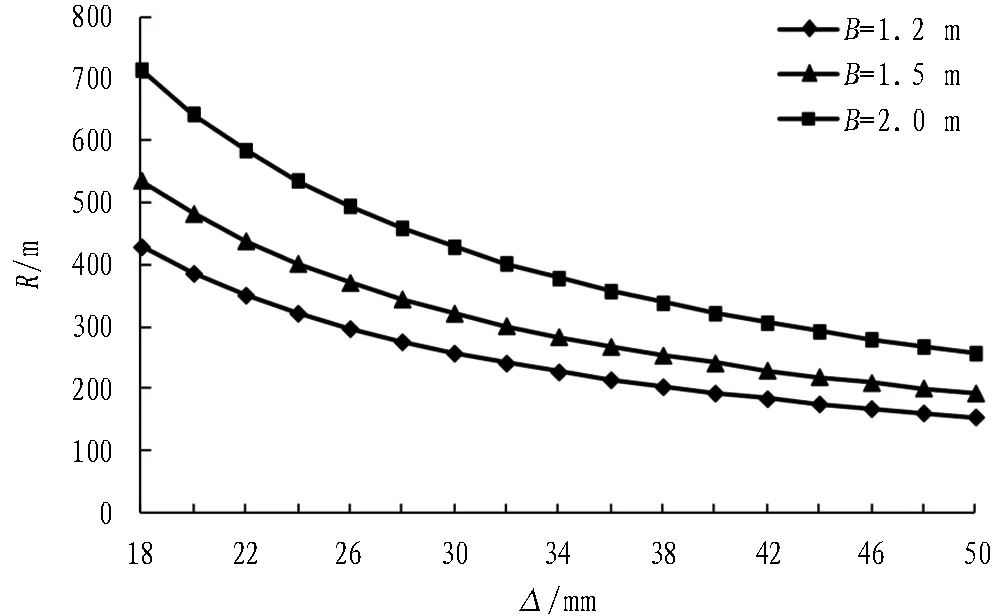
图3管片楔形量对最小拼装曲线半径的影响(D=6 m，拼装点位为12组)

Fig. 3 Effect of segment wedge quantity on minimum assembling curve radius(D=6 m and 12 assembling point positions)

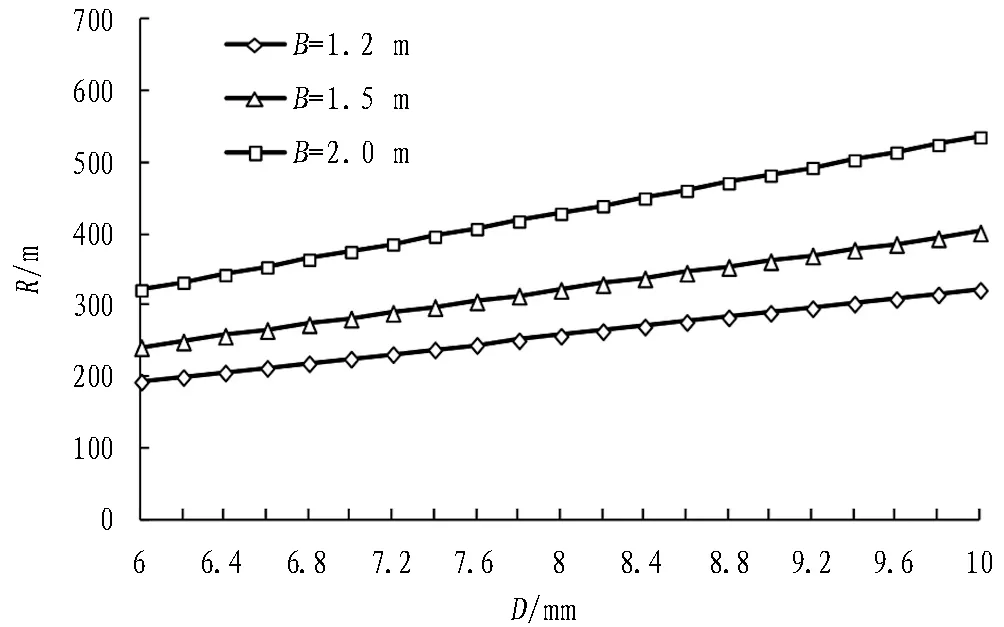
图4管片外径对最小拼装曲线半径的影响(Δ=40 mm，拼装点位为12组)

Fig. 4 Effect of segment outer diameter on minimum assembling curve radius(Δ=40 mm and 12 assembling point positions)

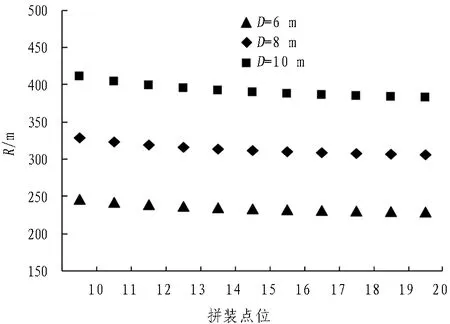
图5拼装点位组数与最小拼装曲线半径的关系(Δ=40 mm，B=1.5 m)

Fig. 5 Relationship between number of assembling point positions and radius of minimum assembling curve radius (Δ=40 mm andB=1.5 m)

在管片构造设计时，几何参数的选择必须保证隧道对线路最小半径的适应性。图6示出针对最小拼装半径的变化范围，环宽分别为1.2 m、1.5 m和2.0 m时的管片外径与楔形量取值的分布情况。设计人员可根据线路设计输入条件，先利用图6对管片的几何参数进行合理组合，后续再综合考虑限界、设备、施工等因素细化管片选型和构造设计。

3 实例分析

以南京地铁某区间线路为例，利用上文所推导的通用环管片排版计算公式进行隧道预拼装，比较环宽B=1.5 m时，外径为6 m和8 m的管片在不同楔形量的条件下，拼装轴线与线路的误差变化。该区间平面曲线半径为450 m，缓和曲线长度为70 m，切线长度为107.32 m，纵断面设计为V型坡，出站后线路先以4.943‰的坡度下坡，坡长634 m，后以3‰的坡度抬升，坡长223 m，竖曲线半径为3 000 m。线路起点标高为1.485 m，竖曲线交点标高-1.232 m。区间长度为857 m，直缓ZH点位于411 m(274环)，圆曲线起点和终点分别位于481 m(321环)和554 m(370环)，缓直HZ点位于624 m(416环)。

(a) 环宽B=1.2 m (b) 环宽B=1.5 m (c) 环宽B=2.0 m

雷达图周向数字表示管片直径，单位为m；竖向数字表示楔形量，单位为mm。

图6管片外径和楔形量针对不同最小拼装半径的组合分布图(拼装点位为12组)

Fig. 6 Distribution of wedge shape quantities under different segment outer diameter and minimum assembling radius(12 assembling point positions)

图7示出采用本文提出的排布计算方法，在楔形量分别为30、40、50 mm时，有效拼装点位12组的通用环管片预拼装150～400环与线路的误差分布情况。其中，图内实直线为D=6 m的误差趋势线，虚直线为D=8 m的误差趋势线。由图6(b)可知，在线路曲线半径为450 m时，环宽1.5 m的管片外径D=6 m的楔形量要求为Δ>21.4 mm，外径D=8 m的楔形量要求为Δ>28.6 mm。可见，2种管片外径类型的3种楔形量(30、40、50 mm)管片均具有线路曲线半径为450 m的拟合能力，但D=8 m管片在Δ=30 mm时已接近最小楔形量。

在图7(a)中，Δ=30 mm时，外径D=6 m的管片能较好地适应线路直线段和曲线段的变化，误差趋势线(实线)为平缓上升趋势线，说明在直线段的拼装误差控制比曲线段较强，最大误差值17.1 mm出现在第2段缓和曲线内；外径D=8 m的管片由于楔形量已接近450 m曲线半径的最小楔形量，误差趋势线(虚线)斜率较大，在曲线段的拼装误差的控制能力较差，出现明显的误差突出点，隧道在圆曲线终点达到误差最大值34.2 mm。

在图7(b)中，Δ=40 mm时，外径D=6 m的管片拼装误差趋势线(实线)平缓上升，最大误差值15.3 mm出现在第2段缓和曲线内，较Δ=30 mm的外径6 m管片最大误差值小，但总体误差分布较分散。对于外径8 m的管片，最大误差值23.5 mm出现在第1段缓和曲线内，误差趋势线(虚线)处于较低值，斜率已大大减小，但仍然出现了3个较明显的误差突出点。

在图7(c)中，Δ=50 mm时，外径D=6 m的管片拼装误差震荡很大，误差趋势线(实线)呈下降趋势，即直线段的拼装误差比曲线段大，最大拼装误差37.8 mm发生在直线段。这是由于通用环管片的楔形量一直存在，大楔形量管片在直线段拼装时会出现“用力过猛”的情况。在管片选型和构造设计时应该避免此类情况，确定楔形量的大小不能只关注曲线段的拟合能力，还需综合考虑线路整体情况，兼顾控制直、曲线的拼装误差。而外径D=8 m的管片则能良好地适应线路变化，最大误差值18.2 mm出现在圆曲线内，误差突出点基本消除。故综合隧道在线路直线段及曲线段的拼装误差，设计线路曲线半径为450 m时，外径6 m管片在3种楔形量中选择楔形量Δ=30 mm能更好控制拼装误差，外径8 m管片选择楔形量Δ=50 mm更合理。

通用环楔形量影响平面直线段拼装的误差，考虑错缝拼装、纵断面坡度等因素影响，最大楔形量可参考如下估算式计算：

(12)

根据《盾构法隧道施工及验收规范》[10]，要求盾构拼装在平面与高程上的误差范围为±50 mm。按规范控制值70%设计，误差e取35 mm，输入管片直径及环宽，由式(12)求出Δmax，并与由图6得到的最小楔形量Δmin求和后取均值，可得到楔形量建议值，如表1所示。在表1中，环宽1.5 m、直径6 m和8 m的管片在曲线半径450 m的楔形量建议值分别为34.05 mm和45.40 mm，与图7中误差分析结果吻合。另外，与实际线路对比后，楔形量建议值与实际工程采用值相近。可见，由图6和式(11)估算出的楔形量建议值具有较高的参考价值。

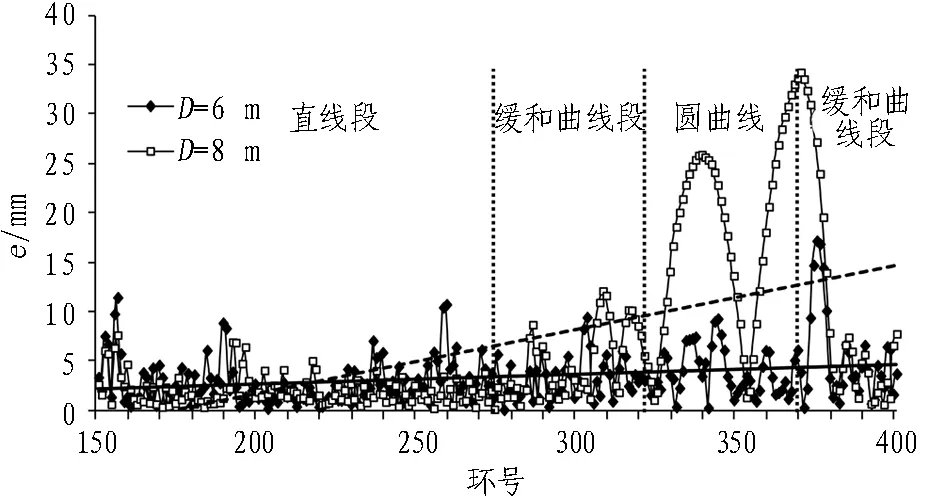
(a) Δ=30 mm

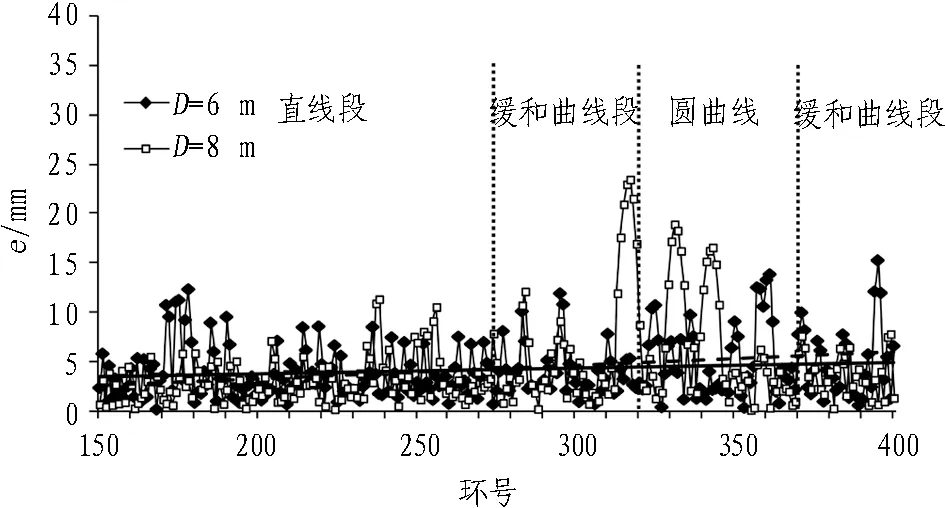
(b) Δ=40 mm

(c) Δ=50 mm

Fig. 7 Error distribution map of completed shield tunnel and design line

表1 楔形量建议值表

4 结论与讨论

本文推导了通用环管片错缝拼装的排版公式，分析了管片主要几何参数对最小拼装曲线半径的影响，为管片选型和构造设计提供适合线路特点的几何参数组合，并以某地铁区间线路作为设计输入进行了管片预拼装，比较了在不同楔形量情况下管片的拼装误差分布，说明了楔形量的合理确定能限制成型隧道发生过大的拼装误差，得到以下结论：

1)盾构管片的外径、环宽、纵向螺栓孔数以及楔形量等几何参数影响着盾构隧道最小转弯半径的大小。在其他几何参数一定时，管片最小拼装半径与管片外径、环宽成正比，与楔形量成反比。而纵向螺栓组增多对管片的最小半径拟合能力并无太大提高。

2)在确定管片楔形量的大小时，需要兼顾控制直、曲线的拼装误差。大楔形量管片虽然能满足小曲线半径的拼装要求，但在直线段或者较缓的曲线段拼装时会出现误差震荡过大，拼装精度难以保证。

3)考虑错缝拼装、纵断面坡度等因素影响，提出了管片最大楔形量估算式，结合线路曲线半径的最小楔形量计算值，得出对应线路的楔形量建议值，并通过与实际线路的应用对比，验证了楔形量建议值计算方法的合理性。

本文虽未分析管片环间张开量、错台等施工随机因素在盾构掘进过程中对管片拼装精度产生的影响，但《盾构法隧道施工及验收规范》中对管片环间张开量、错台等施工偏差已限制在小范围内，在正常施工过程中上述因素对整体拼装精度的影响是轻微的、可控的。故本文所论述的内容对管片选型及构造设计具有一定指引性的工程参考价值。

参考文献 (References)：

[1] 刘凤华. 盾构隧道通用管片拟合排版与管片选型技术研究[D]. 上海： 同济大学, 2007.

LIU Fenghua. Study on the composition and ring selection technology of universal segments for shield-driven tunnels[D]. Shanghai： Tongji University, 2007.

[2] 张志华, 朱国力, 隆泗. 盾构管片排版计算方法的研究[J]. 地下空间与工程学报, 2013, 9(5): 1040.

ZHANG Zhihua, ZHU Guoli, LONG Si. Study on calculating method for composition of segments for shield tunnels[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(5): 1040.

[3] 张忠桢, 骆汉宾, 余群舟, 等. 地铁圆弧形隧道等腰楔形环的拼装与设计： 齐次变换方法[J]. 隧道建设, 2017, 37(10): 1217.

ZHANG Zhongzhen, LUO Hanbin, YU Qunzhou, et al. Design and assembly of isosceles wedged rings for circular metro shield tunnel: a homogeneous transformation method[J]. Tunnel Construction, 2017, 37(10): 1217.

[4] 刘欣, 刘鑫, 柳宪东. 标准环+转弯环的双面楔形盾构管片排版技术研究[J]. 隧道建设(中英文), 2018, 38(5): 805.

LIU Xin, LIU Xin, LIU Xiandong. Study of layout technology for double-sided-wedge shield tunnel segment with standard ring and turning ring[J]. Tunnel Construction, 2018, 38(5): 805.

[5] 储柯钧. 地铁盾构管片在平、竖曲线上的排版探讨[J]. 隧道建设, 2007, 27(4): 20.

CHU Kejun. Array of segment rings for shield-driven metro tunnel[J]. Tunnel Construction, 2007, 27(4): 20.

[6] 宗言海. 地铁隧道常用管片特点与选型计算[J]. 隧道建设, 2009, 29(增刊1): 15.

ZONG Yanhai. Characteristics and model selection calculation of pipe segments often used in metro tunnel[J]. Tunnel Construction, 2009, 29(S1): 15.

[7] 潘国荣, 荣一夫. 盾构通用管片排版与纠偏控制的简化解算[J]. 大地测量与地球动力学, 2014, 34(1): 55.

PAN Guorong， RONG Yifu. Simplified calculation of gemeral segment composition and correction control[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 55.

[8] 吴海彬, 何川, 晏启祥, 等. 通用楔形管片盾构隧道曲线段线路拟合算法及应用[J]. 铁道学报, 2016, 38(10): 90.

WU Haibin, HE Chuan, YAN Qixiang, et al. A study on curve fitting algorithm of curved shield tunnels assembled by universal wedge segments and its application[J]. Journal of the China Railway Society, 2016, 38(10): 90.

[9] 宋成辉. 软土地层地铁盾构通用环管片结构设计研究[J]. 地下空间与工程学报, 2011, 7(4): 733.

SONG Chenghui. Study on structure design for universal shield segments of metro in soft soil[J]. Chinese Journal of Underground Space and Engineering, 2011, 7(4): 733.

[10] 盾构法隧道施工及验收规范： GB 50446—2017[S]. 北京: 中国建筑工业出版社, 2017.

Code for construction and acceptance of shield tunnelling method: GB 50446-2017 [S]. Beijing: China Architecture & Building Press, 2017.