地下工程平衡稳定理论再研究
2019-09-10朱汉华吴志军王迎超
朱汉华, 吴志军, 王迎超, 丁 智
(1. 浙江省公路局, 浙江 杭州 310000; 2. 武汉大学土木建筑工程学院, 湖北 武汉 430000; 3. 中国矿业大学 深部岩土力学与地下工程国家重点实验室, 江苏 徐州 221116;4. 浙江大学城市学院工程学院, 浙江 杭州 310015)
0 引言
地下工程施工过程中容易发生坍塌事件甚至安全事故,通过对大量地下工程施工实践和坍塌事件或安全事故调查分析[1-2],得出如下结论: 1)地下工程“基本维持地层(围岩)原始状态”比“合理发挥地层(围岩)自承能力”更容易判断地下工程结构体系是否满足结构变形协调控制。若满足结构变形协调控制,则结构实际受力变形状态与设计受力变形状态基本一致; 反之,结构实际受力变形状态与设计受力变形状态有差别,容易产生各种意想不到的问题; 2)设计中往往忽视施工过程的结构力学平衡稳定性,连结构力学平衡稳定性都不满足,就更不会满足新奥法了,实际上隧道设计中不但要研究结构整体稳定性,还要研究施工过程中分部结构稳定性; 3)部分工程师往往缺乏类似施工经验,虽然熟记新奥法理念,但忽视了结构力学稳定平衡问题,方法应用不到位,实际还是不满足新奥法。需要明确的是新奥法是一种理念,而结构力学是基石。
很多工程师在技术层面知道如何按照规范进行工程结构设计和施工,但对产生结构病害的结构与力学关系研究多注重力学平衡性,而对协调性研究主要注重变形协调理论、变形协调假设等,而系统研究合理结构构造与力学关系的变形协调控制方法较少,难以保障结构传力介质的适应性和避免结构亚稳定平衡问题。全面研究结构与力学关系才可能避免“亚稳定解”(满足规范,但结构构造欠合理,可能耐久性不够甚至存在特殊风险),而从“可用解”(满足规范,可能合适、保守、特殊情况存在缺陷或风险)提升到“优化解”(优于规范,前沿研究成果或当前优化解决方案,但要防止特殊缺陷或风险),不断寻求结构设计、施工研究等科学问题的真谛。也可简述为工程结构设计阶段就要考虑施工过程每一步都满足稳定平衡与变形协调控制,并在施工过程严格落实和监控工程结构稳定平衡与变形协调控制的核心指标在设计允许范围之内。
实际上,“新奥法”的本质是地下工程建设过程中“合理发挥地层(围岩)自承能力”的设计施工理念与方法,如果结构欠合理,虽然有监控量测或预测控制,还可能发生特殊风险甚至安全事故。地下工程建设全过程必须满足结构稳定平衡与变形协调控制,才能真正“合理发挥地层(围岩)自承能力”和满足建设运营全过程的质量安全要求。地下工程平衡稳定理论的优势是设计中无论采用松弛荷载理论还是现代力学(如有限元)等预先判断地层(围岩)自承能力或计算结构荷载,其中还涉及软岩(土)强度值与初始流变应力值的差异和有效利用软岩(土)高限流变应力值问题,拿出较好的支护开挖方案和应急预案,施工中采用“新奥法”理念支护开挖,并监控量测或预测控制,然后动态调整设计施工方案,“合理发挥地层(围岩)自承能力”和满足结构稳定平衡与变形协调控制,确保地下工程结构质量与安全。
本文统计大量地下工程施工的成功与失败案例,从地下工程结构的受力变形状态稳定性方面出发,研究松弛荷载理论和岩承理论和其他地下工程理论与相应技术的科学本质,及其指导现代地下工程建设实践的意义和价值,探索并建立地下工程平衡稳定理论[3]。以前的研究主要只是针对某一工程而言,本文在总结众多工程实践的基础上,将地下工程平衡稳定理论提炼升华,使其上升到一定的理论高度,具有更强更广泛的适用性,能更好地指导实际工程的实施。与已有的研究相比,取得了长足的发展与进步,为解决新型地下工程问题做出了有益的尝试。
1 工程结构稳定平衡与变形协调控制的物理意义
为了说明工程结构稳定平衡与变形协调控制关系的物理意义,可以通过图1所示重物稳定平衡与变形协调控制关系示意图[4]直观地理解变形协调控制对结构平衡状态稳定性的影响。图1中的重物W由n股绳子悬挂,绳子作用力S1,S2, …,Sn与自重W共同作用处于平衡状态。该平衡状态因为绳索作用力Si和重物W共同作用的变形协调控制关系不同,其平衡稳定状态也不相同,具体表现如下。

图1 多股绳子悬挂下的重物稳定平衡与变形协调控制关系图
Fig. 1 Relationship between stable equilibrium and deformation coordination control of heavy objects under multi-strand rope suspension
1)当重物W受静载荷作用时,S1,S2, …,Sn与W共同作用处于平衡状态,当S1,S2, …,Sn都在各自强度允许范围内系统处于稳定平衡;当出现某个Si超过极限而破坏,此时,剩余n-1根绳索的受力状态会重新分配。在内力重分布过程中,可能出现2种情况: 若内力能够合理转移,剩余n-1根绳索受力仍处于强度范围内,系统将再次平衡;若系统结构设计不当,系统内力不能合理转移,将导致剩余n-1根绳索内力再次超过强度范围而引起断裂,该过程重复出现将引起连锁反应而使系统整体失稳。从能量传递角度看,上述现象可以解释为: 由于重物W的作用,每根绳子内积聚的应变能为Ui(i=1,2,…,n), 此时结构处于稳定平衡。倘若某个绳子内部储存能量Ui已达到其吸能极限而出现断裂,则Ui完全释放。由于系统总体能量不变,则结构变形能将重新分配,将出现2种情况: 若能量能够合理传递,剩余n-1根绳索能有效吸收所有变形能,系统将再次平衡;若结构设计不当,外力做功将再次突破结构储能极限,导致剩余n-1根绳索断裂,引起连锁反应而使系统整体失稳。
2)当重物W受到扰动时,重物W将偏离原始的位置,因而S1,S2, …,Sn的大小将重新分布,只有当S1,S2, …,Sn变形协调(即S1,S2, …,Sn之间的内力能够合理转移)时,且都在强度允许范围内时就处于稳定平衡与变形协调控制状态,系统才能恢复到新的平衡位置。否则,当结构设计不合理时,系统内部受力不能合理转移,S1,S2, …,Sn的重新分布可能会造成某个绳子作用力Si超过极限而破坏甚至引起连锁反应而出现系统整体失稳。从能量分析角度则更好理解: 外界对重物W的扰动将给结构输入一定的能量,只有当结构变形协调(即总体变形能在每根绳子之间能够合理传递)时,且考虑到空气和结构内部耗能机制(例如阻尼、摩擦等),系统才能恢复到原始的位置。否则,当结构设计不合理时,系统内部能量不能合理传递,U1,U2, …,Un的重新分布可能会造成某个绳子无法吸收应有的能量而破坏甚至引起连锁反应从而出现系统整体失稳。
3)当重物W受动荷载作用时,各S1,S2, …,Sn受力不均匀性更加明显,S1,S2, …,Sn与W共同作用的稳定平衡与变形协调控制更加复杂,因为结构输入能量的大小随着外部动荷载作用形式的变化而变化,考虑到空气和结构内部耗能机制(例如阻尼、摩擦等),结构体系在振动过程中也会消耗一部分能量。当结构变形协调,通过外力做功输入到结构体系的能量与系统耗散的能量处于动态平衡过程,系统不会出现能量不断积聚过程。当结构设计不合理,变形不协调时,通过外力做功输入到结构体系的能量总体上大于系统耗散的能量,系统能量不断积聚,导致发散的系统振动,最终出现能量在结构薄弱环节积聚而导致局部破坏甚至引起连锁反应而出现系统整体动力失稳。
一般工程结构力学分析中隐含荷载、变形适应性,实际工程结构首先要稳定平衡,再者结构措施要保障结构变形协调控制,往往实际工作中容易忽视。为了便于理解工程结构稳定平衡、稳定平衡与变形协调控制2个概念的内在联系,将这2个概念对应的工程结构受力分析问题以及理论适用条件归纳总结,如表1所示。
表1变形协调控制与结构平衡状态的关系
Table 1 Relationship between deformation coordination control and structural equilibrium state

状态工程结构受力分析适用条件稳定平衡 采用精确分析法解决工程结构问题 隐含或自然满足变形协调控制 稳定平衡与变形协调控制 先整体控制与细节把握,再用精确分析法解决工程结构问题 构建合理结构体系和合理工法或工艺以及有效过程控制措施等,确保力的合理传递或转移路径等
工程结构只有处于稳定平衡与变形协调控制状态才能存在。对于地下工程结构而言,“基本维持地层(围岩)的原始状态”和“施工过程控制”至关重要。以新奥法等为代表的现代施工技术的核心是“充分发挥围岩的自承能力”,这一提法从力学角度提出了保持围岩稳定的思路,决定围岩稳定性的关键是围岩与支护系统共同作用达到“稳定平衡与变形协调控制”。在实际工程中,地下工程开挖后围岩应力会重分布,特别是存在塑性区时围岩的应力还会产生转移。因此,围岩应力的集中区分布、围岩稳定性可能出现突变点位置的把握是十分困难的,也难以用应力控制手段实现围岩的稳定性判断。在围岩稳定性评价中,关键是要控制变形异常,对Ⅰ级、Ⅱ级、Ⅲ级偏好围岩主要控制块体掉落和块体的稳定平衡,而Ⅲ级偏差围岩及Ⅳ级、Ⅴ级、Ⅵ级围岩主要控制变形协调、不产生有害变形导致坍塌和丧失稳定平衡。“基本维持地层(围岩)原始状态”的理念,直接面对围岩的“稳定平衡与变形协调控制”,从整体稳定的视角出发,既是保持原有围岩与支护系统共同作用达到稳定平衡和控制变形异常,又是“合理发挥地层(围岩)自承能力”的充分必要条件。工程实践中“合理发挥地层(围岩)自承能力”和“基本维持地层(围岩)原始状态”二者理念相同,而“基本维持地层(围岩)原始状态”理念便于实践应用并控制围岩稳定。
地下工程不同的施工工序通常会给岩土体带来不同的受力变形状态。地下工程设计中通常只考虑工程结构完成时的受力状态,而忽视施工过程中的受力变形状态。自承能力好的围岩,在应力重分布后可以重新调节达到稳定平衡,开挖方式对围岩和支护结构的影响不大;但在自承能力较差的岩土体中,施工过程中必须合理把握施工工序,注重过程控制,把握施工过程中岩土体与支护结构的受力变形状态,才能确保其受力变形状态符合设计要求,从而实现地下工程岩土体“基本维持地层(围岩)原始状态”及结构“稳定平衡与变形协调控制”。围绕岩土体的受力变形状态进行研究,地下工程过程控制和时空效应的研究与实践是等效的。要切实落实过程控制,必须注重地下工程建设的时空效应,做到4个及时: 及时支护,及时封闭,及时量测,及时反馈。
2 传统荷载理论
2.1 松弛荷载理论
“松弛荷载理论”由Haim等提出,其核心内容是:稳定的岩体有自稳能力,不产生荷载;不稳定的岩体则可能产生坍塌,需要用支护结构予以支承。这样,作用在支护结构上的竖向荷载就是围岩在一定范围内由于松弛并可能塌落的上覆岩土层的重力γH。这一理论适用于浅埋隧道,但是随着隧道埋深的不断增大,该理论存在许多不合理之处。对埋深较大的隧道,计算得到的压力偏大。
松弛荷载理论曾经产生过重要的影响,作为围岩压力的近似计算方法,应用比较简便。在岩体破碎或浅埋隧道情况下其计算结果仍具有重要的价值,至今仍在一些国家广泛应用。而依据松弛荷载理论统计地下工程围岩塌方规律的规范值大部分可行,但在没有采用变形协调控制手段修正其开挖和支护工法时,对于围岩偏差和偏好的情况存在工程风险和支护过度问题。
2.1.1 围岩破坏的有限区域理念——普氏理论
普氏理论[5]是早期的围岩压力计算理论,虽然在许多情况下其计算结果可能与实际情况有较大的误差,但其围岩破坏的有限区域理念仍然具有重要意义。
这个理论的基本要点是: 1)将岩体看成具有一定黏结力的松散体;2)作用于衬砌上的围岩压力,仅为压力拱与衬砌间破碎岩体的重力,而与拱外岩层及洞室埋深无关。根据普氏理论得到矩形洞室荷载计算图如图2所示。
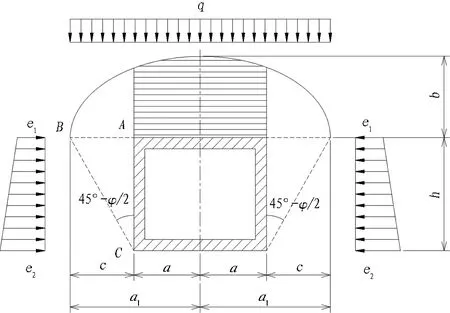
φ为岩体的内摩擦角,°;q为压力拱上的垂直均布荷载,N/m;ei为水平荷载,N/m;b为自然平衡拱的最大高度,m;a1为自然平衡拱的最大跨度,m。
图2压力拱理论计算图
Fig. 2 Theoretical calculation sketch of pressure arch
2.1.2 围岩破坏的稳定平衡理念——太沙基理论
太沙基理论[6]将地层看作松散体,但它是基于应力传递概念而推导出作用于衬砌上的垂直压力,其核心思想是力的平衡。假定在深度为H的岩体内开挖跨度为2b的矩形洞室。开挖后侧壁稳定,拱顶不稳定,可能沿着图3所示的面AB和CD发生滑移,洞顶围岩压力等于上覆岩柱的重力减去侧壁抗剪力。

图3 侧壁稳定时的围岩压力计算图
Fig. 3 Surrounding rock pressure calculation under condition of sidewall stability
开挖后如侧壁不稳定,拱顶不稳定,则按图4所示的面AB和CD发生滑移,计算相应的围岩压力。对于围岩的变形破坏方式假设,太沙基理论可能过于简化或者有不合理之处,但其力学平衡的分析理念在当前的隧道工程实践中仍具有重要的价值。
2.1.3 代表性施工方法
隧道的常规施工方法又称为矿山法[7],因最早应用于采矿坑道而得名。在矿山法中,多数情况下都需要钻孔爆破进行开挖,故又称为钻爆法。从隧道工程的发展趋势来看,钻爆法仍将是今后我国隧道最常用的开挖方法。在矿山法中,可分为以钢木构件支撑的施工方法和采用钻爆开挖加锚喷支护的施工方法。

图4 侧壁不稳定时围岩压力计算图
Fig. 4 Surrounding rock pressure calculation under condition of sidewall intability
基于传统太沙基理论或普氏理论等设计方法的松驰荷载理论是建立在浅埋松散地层和深埋松散岩土体统计值的力学方法基础之上,没有变形协调控制和过程控制概念,也没有体现“合理发挥地层(围岩)自承能力”和“基本维持地层(围岩)原始状态”基本理念。对于相对比较破碎岩体或软土地层,只有满足“基本维持地层(围岩)原始状态”条件,才能达到“合理发挥地层(围岩)自承能力”。对于浅埋松散地层隧道或软土盾构隧道可采用简化计算即荷载结构法思路(对应于松散荷载理论),产生的误差在支护结构强度允许范围之内;但施工工法和过程控制措施应采用地层结构法思路(对应于岩承理论),实现地层与支护结构共同作用达到“稳定平衡与变形协调控制”,消除风险隐患,确保受力安全。
2.2 岩承理论
2.2.1 基本原理
“岩承理论”是一种现代支护理论。其核心内容是: 稳定围岩是因为岩体有自承能力;不稳定围岩丧失稳定是有一个过程的,如果在这个过程中给围岩提供必要的帮助或限制,则围岩仍然能够进入稳定状态。这是一种比较现代的理论,它已经脱离了地面工程考虑问题的思路,而更接近于地下工程实际,近半个世纪以来被广泛地推广应用。
传统“松弛荷载理论”更注重结果和对于结果的处理;而现代“岩承理论”则更注重过程和对过程的控制,即对围岩自承能力的充分利用。由于有此区别,2种理论在原理和方法上各自表现出不同的特点。以这2种理论为指导的施工方法也截然不同,对隧道围岩稳定产生的影响也不尽相同。基于“岩承理论”的围岩支护与围岩位移关系如图5所示。在一定范围内,允许围岩变形量越大,需要的支护力就越小,否则会出现相反的情况。但要使围岩不发生破坏,必须限制变形的发展。
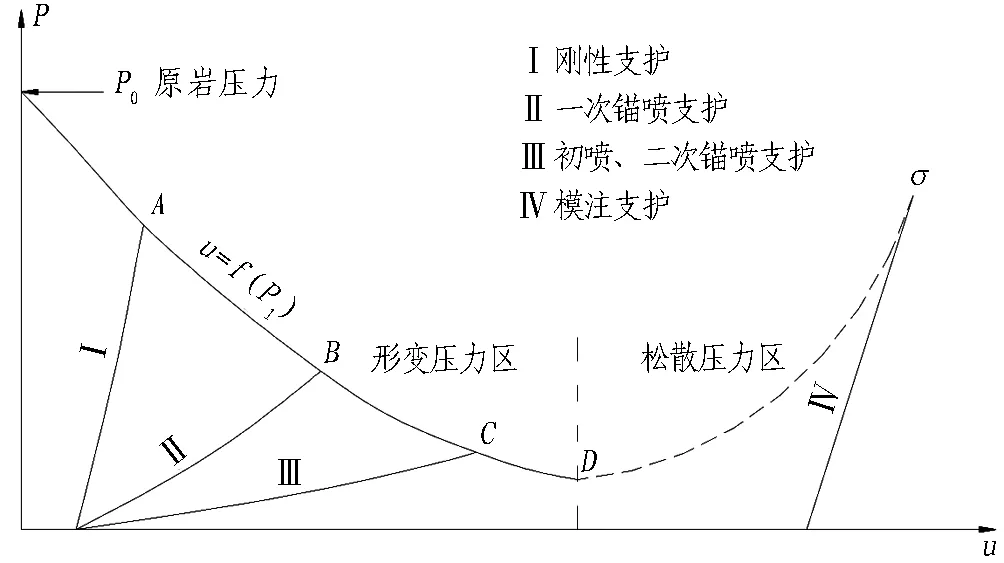
图5 围岩位移支护特性曲线
Fig. 5 Displacement supporting characteristic curve of surrounding rock
新奥法核心概念广泛应用于隧道及地下工程设计施工等实践过程中。但是基于围岩位移支护特性曲线进行围岩支护设计存在一个重要问题: 支护特性曲线上的D点是理论上存在而实践上无法把握的点,围岩位移支护特性曲线虽然解决了隧道围岩结构受力平衡问题,但是较难把握隧道围岩结构的平衡稳定性问题。依据“岩承理论”的新奥法源于硬岩,虽然强调了硬岩与软岩应用有区别,但在不良地质条件下,对于分支点失稳工程问题,很难把握围岩与支护结构共同受力平衡状态的稳定性,地下工程施工安全事故与衬砌开裂现象就说明了其存在的工程风险。
2.2.2 代表性工法理念——新奥法
新奥法是由奥地利土木工程师Rabcewicz等在20世纪60年代总结隧道建设实践经验的基础上创立的。自提出后,该理论基础不断得到完善,隧道支护技术手段不断丰富,在世界隧道设计和施工中获得广泛的应用,当前已被国内外作为隧道结构设计和施工的重要方法。新奥法的理论基础是“合理发挥围岩自承能力”,以喷射混凝土、锚杆加固为代表和量测技术为主要特征的新奥法,尽可能保护围岩原有强度、容许围岩变形但又不致出现强烈松弛破坏、掌握围岩与支护结构变形动态的隧道开挖与支护原则,使围岩变形的外荷载与限制变形的结构支护抗力保持动态平衡,该施工方法具有很好的适用性和经济性。
新奥法是建立在岩石试验力学的基础之上,其结构力学分析方法不很明确,使用中容易忽视,使得支护结构不合理。要体现“合理发挥地层(围岩)自承能力”和“基本维持地层(围岩)原始状态”理念,需要深厚力学理论知识和丰富类似工程实践经验相结合,才能真正落实岩承理论的精髓,确保围岩与支护结构共同作用达到“稳定平衡与变形协调控制”。在“合理发挥地层(围岩)自承能力”和“基本维持地层(围岩)原始状态”即“变形协调控制”理念基础上,建立适用多种岩土体结构特征的广义力学稳定平衡方程,重视合理开挖工法、支护结构措施及施工过程控制等研究,确保围岩与支护结构共同作用达到稳定平衡与变形协调控制,这也是地下工程结构设计和安全分析的基本要求。在不良地质条件下,地下工程施工过程中地层(围岩)与支护结构共同作用力的平衡稳定性和变形协调性有时不一定满足,施工单位也难以有效控制,往往产生施工安全事故,只好要求在规划和设计过程中加以考虑,才能避免类似事故。
3 地下工程平衡稳定理论
3.1 隧道有效承载结构层控制围岩荷载转移规律
3.1.1 围岩应力会向深部转移
通过适当开挖与支护,围岩应力会逐渐向深部转移,减轻表部围岩应力集中导致变形或破坏。天然洞穴如图6所示,该洞穴高200 m,宽150 m,此洞穴尺寸会逐渐扩大,这是由于周边围岩产生了塑性破坏,使得围岩的应力集中区向深部逐渐转移。

图6 天然洞穴
3.1.2 隧道有效承载结构层控制围岩荷载转移规律
隧道围岩的稳定是隧道围岩与支护系统共同作用的结果,如果施工开挖支护过程不合理,平衡状态就会发生转换。当隧道采用预支护而使围岩基本保持原始状态时,有
P1cosα1+P2cosα2=T=W。
(1)
式中:P1、P2为围岩之间相互支持力,N;W为重力,N;T为支护抗力(T起到合理发挥P1、P2的作用),N。
破碎围岩等特殊地质隧道开挖后自稳时间短,易形成冒落。通过施加预支护,预支护结构、初期支护和二次衬砌形成支护结构体系共同承载。采用浅埋暗挖法或类似软土隧道盾构施工原理的预支护,可以防止松弛坍塌和产生松弛压力。但其机制与锚喷支护不同,可参照普氏理论和太沙基理论进行设计。由于破碎等特殊地质围岩自稳能力差,且常常伴有地下水的作用,为安全起见,不考虑围岩的内摩擦角φ和黏聚力c值(即c=φ=0)的作用,仅考虑由于预支护而不产生有害松弛的围岩之间相互支持力P1和P2的作用(见图7)。
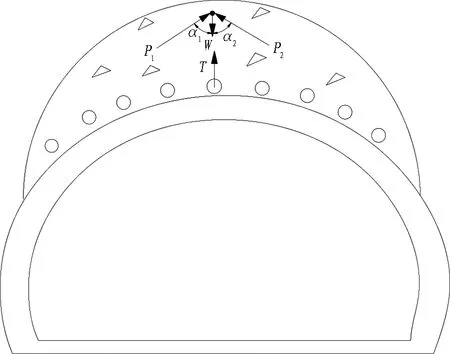
图7 隧道有效承载结构层控制围岩荷载转移规律
Fig. 7 Load transfer law of surrounding rock controlled by effective bearing structure layer of tunnel
当隧道围岩没有采用预支护而发生较大松弛或塌方时,则有T≤W。也就是说,对于破碎等特殊地质围岩必须采用预支护技术才能确保支护结构承受的围岩压力是形变压力而不是松弛压力。同时,施作预支护时也必须考虑到预支护的刚度和开挖后喷射混凝土的时间,即时空效应,这些都影响特殊地质围岩的变形,即影响围岩压力的大小和分布情况。隧道有效承载结构层控制围岩荷载转移规律,选取适当的预支护刚度和喷射混凝土的时间等及时形成隧道有效承载结构层十分重要。
3.2 地下工程平衡稳定理论的建立
不论松弛荷载理论还是岩承理论,在实际地下工程应用中有优势也有不足,甚至存在安全隐患,本文通过大量岩石、土体、岩土混合体地下工程结构应力变形状态试验研究得出。岩土体地下工程结构控制安全边界线如图8所示。图5中P0-D段与图8中控制安全边界线相对应,而图5中D-σ段在地下工程设计施工中没有应用意义。在控制安全边界线内,能有效利用高限流变应力值,其对建立地下工程平衡稳定理论具有较好的实践意义。

(a) 应变边界
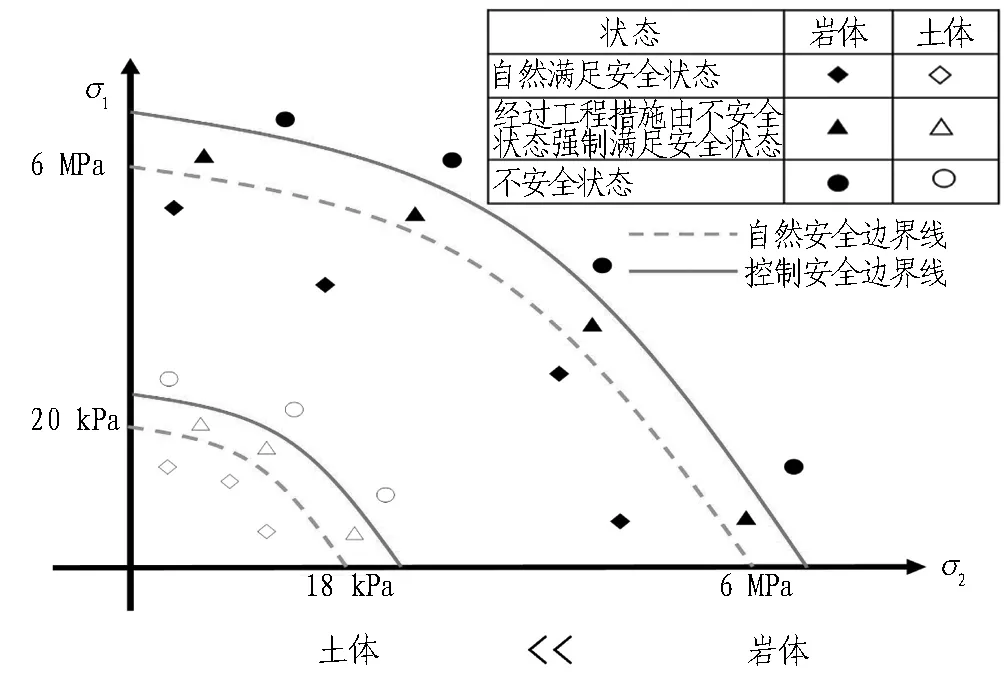
(b) 应力边界
Fig. 8 Safety boundary line of structure control for underground engineering of rock and soil mass
以淤泥质软土和砂岩为例,对比了土体或岩体在工程应用中应力控制方法和应变控制方法的工程力学特性(见图8)。虚线为岩体或土体对应原始状态的安全控制边界,即自然安全边界线。虚线内部的受力或变形状态为安全状态(四边形所示状态),超出虚线即认为岩体或土体发生破坏。该状态可以通过工程措施得到一定程度的提高,例如在软土中注浆、在岩体中加锚杆锚索,如果工程结构满足变形协调控制,安全容许范围就会扩大至实线范围。此时某些原本不安全状态就转化为安全状态(三角形所示状态),即通过工程措施能够有效利用高限流变应力值。值得注意的是,工程措施实施过程必须满足变形协调控制,否则会产生局部应力过大或者变形过大导致结构失稳。只有这样,才能保证地下工程结构力的合理传递或转移、稳定平衡与变形协调控制。
由图8还可以发现,地层岩土应力大的应变反而小,因此结构变形协调控制对不良岩土地层地下工程控制变形尤为重要。地下工程稳定平衡状态可以抽象并提炼出隧道围岩自承力P、支护抗力T和围岩原岩压力P0三者之间的力学关系,真实反映隧道“围岩-支护”体系在开挖与支护(含预支护)过程中的互动过程和相互作用。建立地下工程建设工程平衡稳定理论将有助于解决地下工程设计计算方法的合理选用和施工方案的合理制定。
隧道施工开挖形成新的临空面,导致隧道围岩在径向上产生应力释放,而远离隧道地层的应力状态并不发生变化。不失一般性,考虑均匀地应力场,用P0表示原岩压力。围岩与支护共同作用如图9所示。从静力学的原理可知,P0由“围岩-支护”结构体系的承载力来平衡。
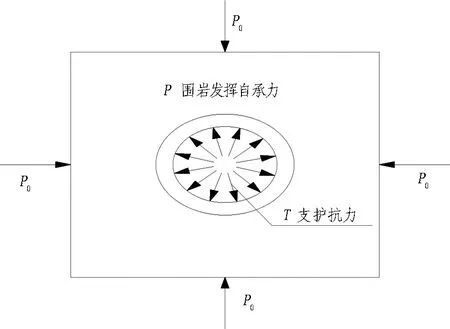
图9 围岩与支护共同作用
隧道预支护力[8]不只是支护结构对围岩的作用力,它是由围岩结构自承能力和支护结构直接对围岩提供的支护抗力共同组成的。围岩结构自承能力可以通过预支护措施和采取合理开挖措施得到维持。
为了更好地理解预支护力,将其定义为
F=T+P。
(2)
式中:F为预支护力,N;T为支护抗力,N;P为围岩自承能力,N。
当预支护力大于使围岩发生过大变形或破坏的力时,隧道围岩处于稳定平衡状态。根据围岩稳定的一般原理,地应力是使围岩发生变形和破坏的根本动力[9],是使围岩失稳的“力源”。隧道预支护技术可进一步表述为: 预支护力F要始终保持大于或等于隧道施工前保持原始岩体稳定平衡的原岩压力P0,围岩处于稳定平衡状态,即
F≥P0。
(3)
式(3)普遍适用于解决地下工程稳定平衡问题,各种理论表现形式,可以随着“具体问题具体分析”而变化,但式(3)是不变的。
地下工程平衡稳定理论的力-位移特征曲线图如图10所示。其总体可表述为如下形式: 1)自承能力好的完整围岩,这种完整围岩自承能力比较大,可以提供维持围岩稳定所需要的承载力,如图11(a)所示,即使不采取任何支护措施,围岩也能自稳,可以取消系统锚杆,自然满足式(3),对应于挪威法。2)有一定自承能力的围岩,这种围岩的预支护原理的曲线如图11(b)所示,采用新奥法施工,容易满足式(3);或用有限元初步计算P0,然后根据地质情况折算P,则可以初步估计T值,也可以满足式(3),对应于新奥法。3)自承能力差的破碎围岩或软弱围岩,如图11(c)曲线所示,这种破碎围岩的自承能力相对较小而且在隧道开挖后会迅速下降,围岩形变压力迅速转化为松弛压力,围岩很快进入松弛状态,即很快从非稳定平衡状态向失稳状态转化,所以要求开挖前提供预支护或超前支护,以改善围岩的原始状态提高自承能力,这时围岩自承能力P约为0,系统锚杆不起作用,则要求T>P0,对应于新意法; 4)其他情况可参考式(1)、(2)、(3),并依据地下工程平衡稳定理论执行。

图10 地下工程平衡稳定理论的力-位移特征曲线图
Fig. 10 Force-displacement characteristic curves of equilibrium and stability theory for underground engineering

(a) 围岩(对应于挪威法)
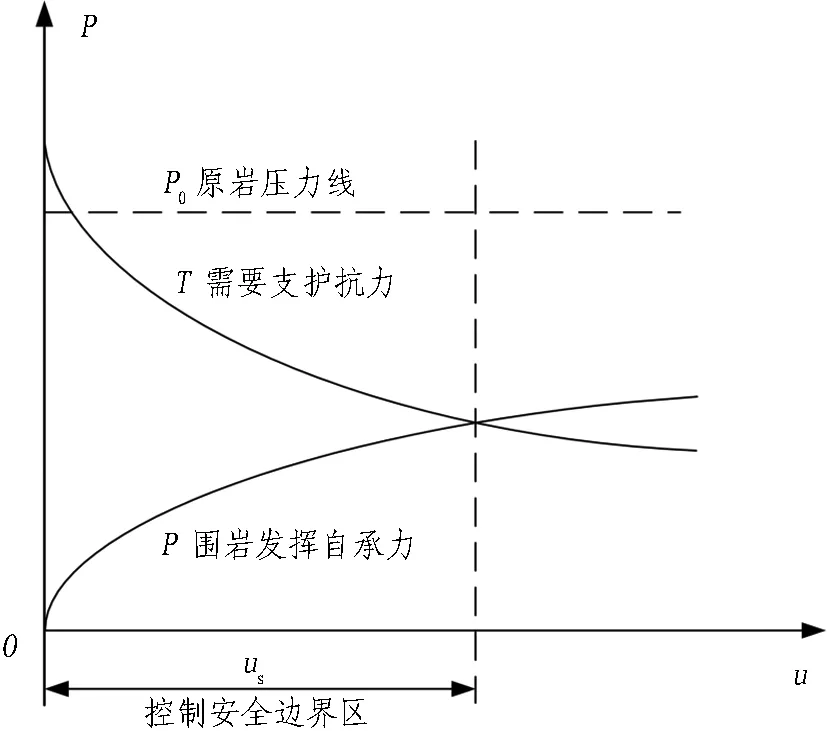
(b) 一般自承能力的围岩(对应于新奥法)
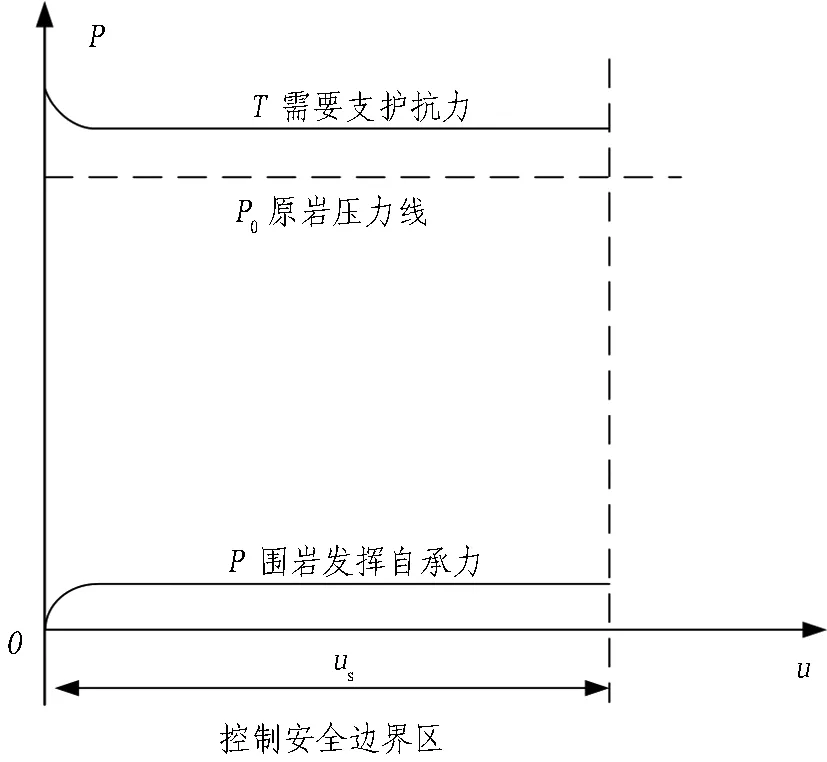
(c) 自承能力很差的围岩(对应于新意法)
图11地下工程平衡稳定理论的力-位移特征曲线3种阶段特例图
Fig. 11 Three stages of force-displacement characteristic curves of equilibrium and stability theory for underground engineering
地下工程平衡稳定理论既反映了传统“松弛荷载理论”和现代“岩承理论”的基本内容,又拓宽了平衡稳定性等内容,是地下工程平衡稳定性的新认识、新理念。该成果基于规范但又宽于规范,在已有地下工程建设理论的基础上,把平衡稳定理论应用于地下工程,建立了更加全面的地下工程平衡稳定理论,同时可以较好解释许多工法和理念的合理性,如取消系统锚杆、合理开挖与支护技术等,以便更好地指导地下工程设计与施工。采用基本力学(理论力学、结构力学、能量增量法等)处理复杂问题一定要先从系统角度理解事物并从整体上加以把握,再从整体与局部的关系把握问题,统筹考虑各方面因素,深入分析围岩、环境、支护系统相互作用之间的力学或能量增量模式(F>P0或ΔU>ΔT(即应变能增量大于外力做功增量))[10-12],主要状态符合基本力学或能量增量关系或通过合理刚度支护系统达到“基本维持地层(围岩)原始状态”和“稳定平衡与变形协调控制”,并把复杂力学问题转化为简单力学问题,就可应用基本力学解决地下工程问题。
总之,工程实践揭示了隧道有效承载结构层控制围岩荷载转移规律,建立了地下工程平衡稳定理论,兼容了新奥法、挪威法、新意法等思想,便于根据围岩承载能力不同阶段,分类预防和控制地下工程质量和安全。另外,地下工程平衡稳定理论拓宽了研究与应用范围: 例如“松弛荷载理论”可以和现代工法结合,“岩承理论”可以和传统工法及更多现代工法结合,“松弛荷载理论”与“岩承理论”也可以拓宽理念或相互融合(完善软土盾构施工理念等),更加适应复杂环境和复杂结构,再和传统工法及更多现代工法结合,能进一步扩大其应用范围。实践发展要求理论创新,犹如计算机系统主板把许多不同功能硬件板卡有机组合起来一样,地下工程平衡稳定理论基于力学分析研究地层支护结构系统的力学状态,用平衡稳定理论把传统“松弛荷载理论”和现代“岩承理论”的基本内容有机组合起来,同时拓宽了许多方面内容,以丰富地下工程平衡稳定理论,全面体现地下工程平衡稳定性的根本内涵,即F>P0或ΔU>ΔT。
3.3 地下工程平衡稳定理论的应用
地下工程结构体系满足“变形协调控制”条件的判别方法: 现有工程材料的强度破坏准则,无论是经典的摩尔-库仑准则,还是双剪应力屈服准则,乃至统一强度理论,均以应力作为衡量标准。但是对于复杂的地下工程,按工程力学分析结果和应力强度标准判断,有时理论上整体满足条件,实际工程结构仍有可能存在一些问题甚至安全隐患,因此利用传统破坏准则判别结构是否安全不全面或不够全面,还应该增加变形控制条件。对于简单结构体系变形具有确定性,不会产生畸变,但是对于复杂工程结构有时由于构造不合理,容易产生变形畸变等,出现实际状态与设计状态不符。简而言之,对于没有变形协调问题的材料单体或者简单结构,因为已经隐含变形协调条件,所以利用现有判断准则不会出现问题。但是对于复杂结构,并不一定符合变形协调控制条件,所以利用现有判断准则很可能产生变形畸变,进一步影响应力的重分布使之与设计状态不符,导致结构积累损伤甚至破坏。
对于复杂工程结构稳定平衡与变形协调控制问题,尽管本质因素是判断结构实际受力变形状态稳定性或者分析结构是否超过设计受力变形状态[13],但在实际工程应用中,常采用具体的、易测量的变量(如变形量、自振频率等)来衡量变形状态稳定性。
地下工程结构也可用围岩是否满足或有效控制“基本维持岩土体的原始状态”条件来判断地下工程结构体系是否满足变形协调控制条件。若满足变形协调控制条件,则结构实际受力变形状态与设计受力变形状态基本一致;反之,结构实际受力变形状态与设计受力变形状态有差别,容易产生各种意想不到的问题。
工程结构体系设计过程中,先借鉴经典工程结构构造特征,初步设计合理工程结构体系[14],一般情况能满足“变形协调控制”条件;复杂或特殊情况可用模型或大比例尺试验进一步验证。
“力和能量要有相应物质载体,并具有相应传递或转换路径”,结构“稳定平衡与变形协调控制”和“能量合理转换”是统一的,结构变形协调控制又是能量法和力法或位移法结构分析的必要条件。确保“力、变形、能量”按设计路径传递并按设计方式转换是结构稳定、安全、合理的基本要求,也是维持设计形式不产生有害过程的基础。根据实际情况,分别从“力、变形、能量”3要素中的1个或几个要素入手进行优化,可更好地控制地下工程结构行为。而确保结构的“稳定平衡与变形协调控制”,不仅需要目标控制,更需要围绕目标实现结构安全合理的过程控制,否则结构就会不稳定或破坏。通过对大量国内外经典历史工程考察、现代力学逻辑分析与判断等可以得出结论: 地下工程围岩与支护结构共同作用,在建设使用全过程都必须满足稳定平衡与变形协调控制,使得各受力的组合结构系统由组合或单体受力体转变为整体共同受力,否则会改变原始力学平衡形式或出现非预期的新的力学平衡形式,甚至丧失稳定性;对于无法实现变形协调控制的多个独立受力单元的地下工程组合结构系统,避免连接部分开裂是重点,例如连拱隧道与小净距隧道及多个独立平行斜交连续梁桥,要提高他们的受力独立性。平衡稳定理念就由稳定平衡拓展到稳定平衡与变形协调控制,包括“合理发挥地层(围岩)自承能力”、F>P0或ΔU>ΔT,以及延伸拓展“基本维持地层(围岩)原始状态”、开挖能量控制技术、强预支护技术、受力独立性综合技术、变形协调控制技术等,以便于更加全面研究地下工程建设安全等问题。
实现稳定平衡的目标,需要现代施工技术(如新奥法、浅埋暗挖法、挪威法、新意法等)和传统施工技术(如矿山法、太沙基理论、普氏理论等)及适用特殊环境地下工程的其他有效工法作为辅助手段,以及开挖能量控制技术、强预支护技术、受力独立性综合技术、变形协调控制技术等隧道工程建设的技术措施。只有掌握其指导思想和技术措施,才能真正应用好地下工程平衡稳定理论。
4 结论与建议
本文在大量工程实践和试验的基础上,揭示了地下工程有效承载结构层与围岩荷载转移规律之间的关联性,建立了地下工程平衡稳定理论和创新了4项关键技术,兼容了新奥法、挪威法、新意法等的基本思想,主要结论与建议如下。
4.1 地下工程荷载转移规律和变形协调控制方法
通过大量地下工程实践、观察、试验、统计等,揭示了地下工程有效承载结构层与围岩荷载转移规律之间的关联性,类似围岩开挖卸荷破坏的能量机制,为建立地下工程平衡稳定理论与关键技术打下基础。可指导围岩稳定性评价计算及加固设计,为利用地下工程开挖能量释放来平衡围岩稳定提供了变形协调控制方法基础。
4.2 地下工程平衡稳定理论体系与关键技术
面对不同地质地段导致的地下工程施工中的坍塌、渗漏水、地层变形过大等施工难题,在传统工程结构平衡稳定理论的基础上,按照工程结构变形协调控制方法,融合“松弛荷载理论”和“岩承理论”的优势,创建了地下工程平衡稳定理论体系和配套关键技术。在国内外首次兼容了新奥法、挪威法、新意法等的基本思想,可根据围岩承载能力不同阶段,分类预防和控制地下工程质量和安全,确保地下工程施工质量与安全。
4.3 地下工程围岩变形协调控制等新技术
开发了挤压大变形围岩隧道近似全断面开挖与让压-刚性联合支护设计施工方法、浅埋下穿高速公路大断面隧道的施工方法、双侧偏压小净距隧道施工方法等多个新方法和隧道坍腔充填泡沫、连拱隧道结构优化设计等多个新型结构的地下工程变形协调控制新技术,确保地下工程平衡稳定理论体系与关键技术解决实际问题更加实用可靠。
本文虽然对地下工程平衡稳定理论提炼升华,使其上升到了一定的理论高度,具有更强、更广泛的适用性,能更好地指导实际工程的实施,但由于地下工程的复杂性与多样性,实际施工过程中往往会遇到意想不到的困难,建议具体问题具体分析,这样才能更好地运用地下工程平衡稳定理论,并使其不断丰富与发展。
