土岩起伏地层地铁隧道受上部卸荷影响的变形响应研究

张建斌

(厦门路桥工程投资发展有限公司, 福建 厦门 361026)

0 引言

近年来，越来越多的基坑工程在运营地铁隧道邻近位置或上方进行施工，既有隧道受上部卸荷影响的变形响应分析已成为工程研究的热门问题之一。厦门海沧海底隧道在石鼓山立交段上穿地铁1号线区间隧道，分析和控制上跨基坑开挖卸荷对下卧地铁隧道的影响对工程实施及确保地铁1号线的安全显得尤为重要。

目前，国内研究基坑开挖对地铁变形影响的方法主要包括数值分析方法[1-8]、理论分析方法[9-10]和实测分析方法[11-12]。在数值分析方面，徐凌等[7]通过数值模拟及实测数据分析得出软土地区基坑开挖引起的隧道纵向变形曲线基本呈高斯正态分布，隧道变形影响范围为基坑沿隧道纵向开挖长度的2～3倍； 薛彦琪等[8]通过MIDAS GTS软件对考虑坑底止水帷幕受浮力作用及地下水渗流条件下的坑底回弹和隧道隆起位移进行分析，得出基坑开挖卸荷影响深度约为基坑开挖深度的1.6倍，抗浮锚索对坑底回弹有明显的约束作用。

在理论分析方面，周泽林等[9]将软土地基考虑为3参量 H-K 黏-弹性体，推导了自由边界半无限黏-弹性空间体在内部集中荷载作用下的 Mindlin 时域解，并将隧道看成Pasternak 黏-弹性地基上的欧拉伯努利长梁，推导得到隧道纵向附加变形和内力公式； 陈郁等[10]采用Mindlin经典理论解推导得出由开挖卸荷引起的隧道结构的附加应力，并根据弹性地基梁理论推导出隧道隆起计算公式。以上利用理论分析得出的竖向隆起变形曲线均符合高斯正态分布。

在实测分析方面，陈郁等[11]结合工程实例，利用现场实测数据，分析了基坑开挖对下卧隧道的影响，其认为土体的回弹会引起隧道的变形，隧道的最大隆起点接近基坑开挖的中心处，隧道变形曲线近似为正态分布； 魏纲[12]收集了14个国内基坑工程实例的实测数据，对数据进行统计分析，提出了隧道隆起值的经验预测公式，认为隧道的收敛变形由“水平向拉伸、竖向压缩”向“水平向压缩、竖向拉伸”转变。

以上研究均是针对软土地区盾构隧道，而海沧海底隧道上跨地铁1号线段岩面起伏较大，下卧的地铁区间隧道采用矿山法施工。关于起伏花岗岩复杂地质条件下上部基坑开挖卸荷对矿山法地铁隧道影响的研究较少。起伏花岗岩地层中不同的土岩分界面深度造成了不同的隧道变形结果。土岩分界面深度不同，岩土刚度沿深度的分布则不同，故岩土分界面对隧道变形的影响实质就是刚度对隧道变形的影响，这使得在土岩起伏地层中开挖基坑引起的邻近隧道变形相对于软土地区具有明显差异。

本文针对厦门土岩复合地层中基坑施工对下卧地铁隧道变形的影响问题，提出基于Boussinesq解与Mindlin解的半解析预测方法，计算获得不同基岩面埋深对隧道隆起的影响规律，并拟合提出考虑岩面埋深对隧道隆起变形影响的简化预测公式。为确保施工安全，开展基坑施工全过程中隧道左右线的竖向变形人工和自动化监测，分析土岩起伏地层条件下基坑开挖引起的隧道变形规律，以期为今后类似工程提供参考。

1 工程背景

1.1 工程概况

厦门海沧海底隧道上穿地铁1号线区间隧道。基坑沿地铁轴线宽度为38.5 m，垂直于隧道轴线方向宽约40 m，开挖深度为13.5 m左右。地铁1号线区间隧道采用矿山法施工，为单洞单线马蹄形断面，隧道中心线埋深约23 m，拱顶埋深约20 m，衬砌顶部距离围护桩底最小约为2.6 m，距离坑底最小约为7 m。隧道断面净空约为5.6 m，断面净跨约为5.2 m。支护结构采用复合式衬砌，初期支护采用钢筋网、格栅钢架及喷射混凝土联合支护，二次衬砌为防水钢筋混凝土结构。上跨基坑和地铁隧道的位置关系如图1所示。围护桩采用φ1 000 mm@1 200 mm的钻孔灌注桩，隧道上方钻孔灌注桩桩长15 m，距离隧道拱顶约2.4 m，隧道两侧维护桩桩长21 m。基坑止水采用φ800 mm@1 000 mm高压旋喷桩止水帷幕，旋喷注浆压力为25 MPa。考虑到隧道上方嵌固深度不足，故设置3道内撑，第1道为混凝土支撑，第2道、第3道为钢支撑。基坑底板厚1.8 m。地铁1号线隧道埋深约为20 m，衬砌顶部距离围护桩底最小约为2.6 m，距离坑底最小约为6.4 m。

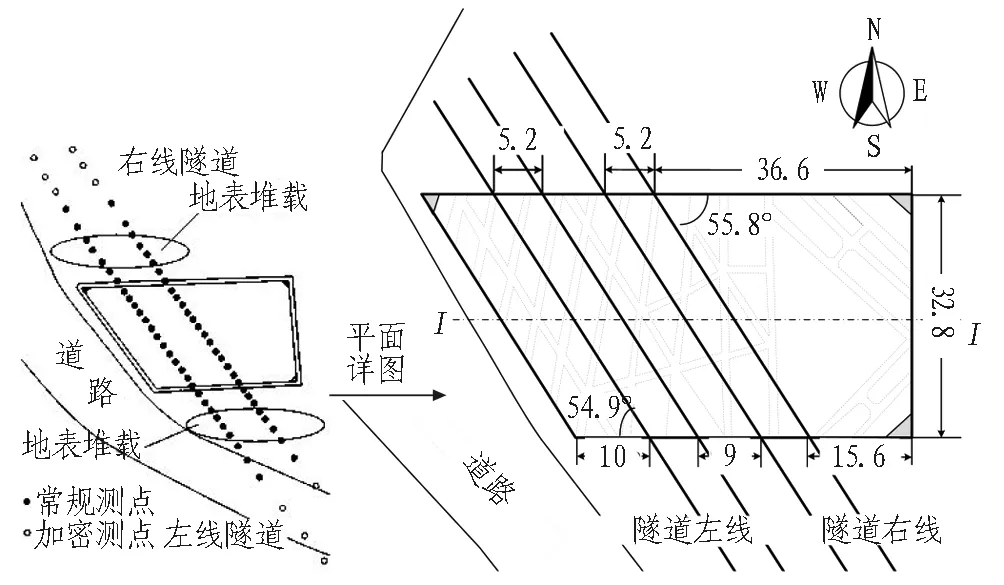
(a) 平面图

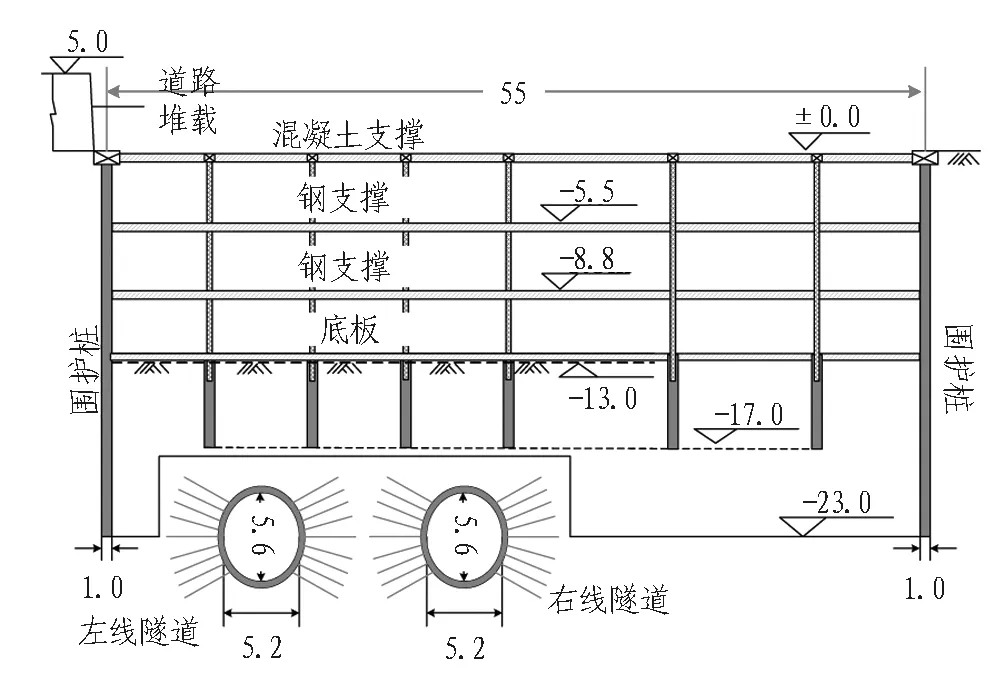
(b) I-I剖面图

Fig. 1 Location relationship between foundation pit and metro tunnel (unit: m)

1.2 工程地质条件

根据地质勘察报告，场区地质条件复杂，主要体现在2个方面： 1) 场区地层为典型的土岩复合地层，既包含与软土地区性质相似的杂填土、粉质黏土、残积土土质地层，又包含全风化、中风化岩等由花岗岩风化产物组成的岩质地层。基坑主要位于土质地层中，而隧道大部分位于风化岩层中。2) 场区土岩分界面起伏不定，沿双线隧道地层分布呈现明显差异，土层及岩层分界明确，左线隧道与右线隧道之间亦展示了截然不同的地层分布剖面。在基坑范围内场区地层包括： ①1杂填土，②3粉质黏土，③残积砾质黏性土。坑底位于残积砾质黏性土中； 坑底下土层为⑤1全风化花岗岩、⑤2-1砂砾状强风化花岗岩和⑤2-2块状强风化花岗岩; 地铁区间隧道拱顶位于⑤2-1砂砾状强风化花岗岩中，隧道洞深大部分位于⑤2-2块状强风化花岗岩中。地铁隧道左右线地质纵剖面图如图2所示。由图2可以看出，隧道左右线地质差异比较大。地铁区间隧道各土层物理力学指标见表1。

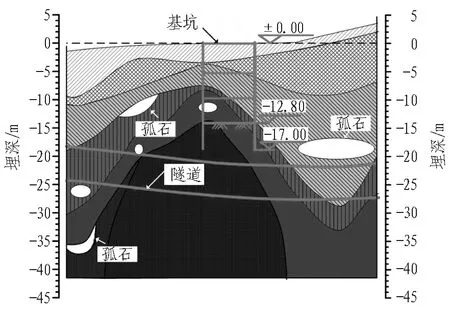
(a) 左线隧道

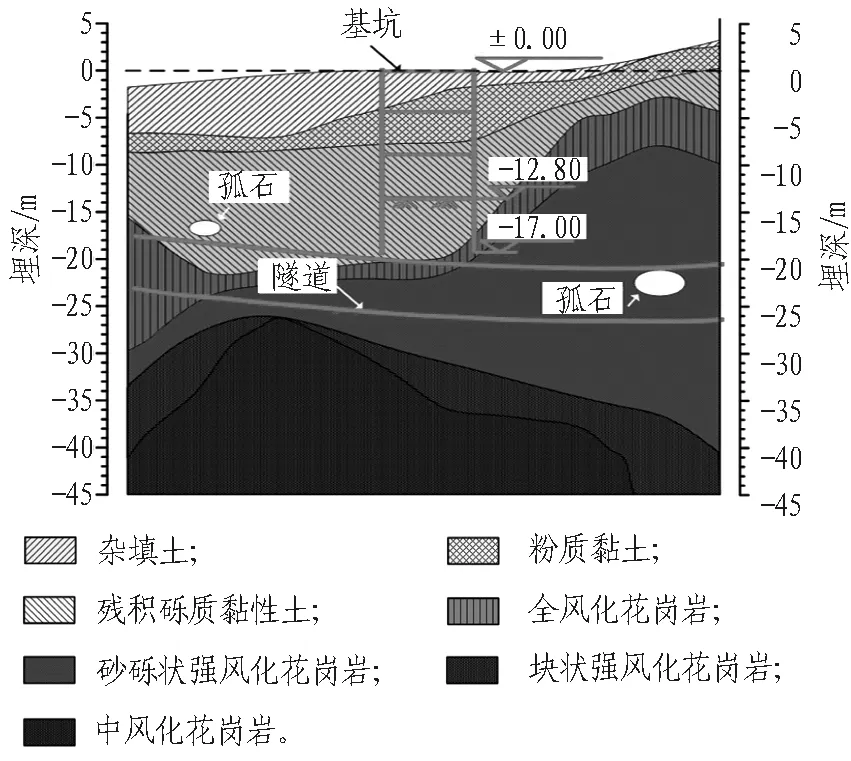
(b) 右线隧道

Fig. 2 Geological profile of left and right lines of metro tunnel (unit: m)

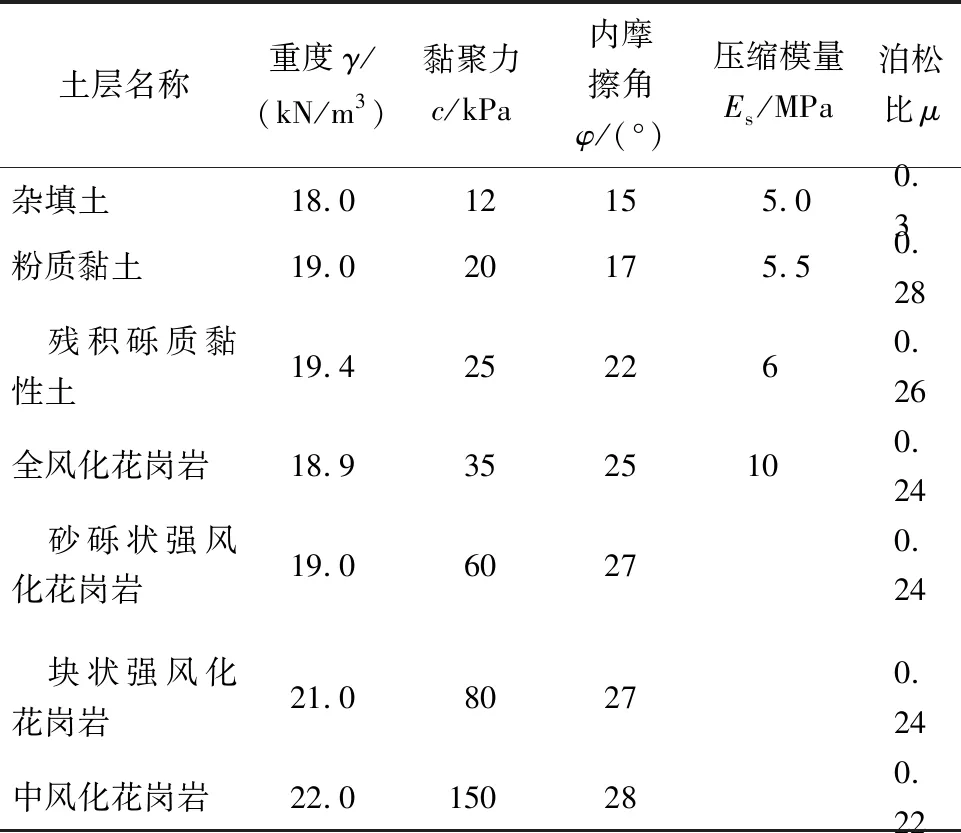
表1 地铁区间隧道各土层物理力学指标

1.3 施工工况

基坑采用明挖法施工，分4层开挖，第1层开挖约1 m，然后施工混凝土支撑；第2层开挖至地面以下7 m，安装第1道钢支撑；第3层开挖至地面以下10 m，安装第2道钢支撑；第4层开挖至坑底，施工混凝土垫层和底板。

2 基坑开挖对下卧隧道变形影响的半解析预测方法

基坑开挖引起隧道隆起是应力释放引起土体回弹与隧道抗力共同作用的结果。理论计算和数值模拟是研究开挖引起下卧隧道变形常用的2种方法。理论计算具有计算效率高、成本低等特点，因此，被广泛应用于施工前期的变形预测。本文基于Boussinesq解和Mindlin解，将隧道简化为等效连续地基梁模型，建立变形控制方程，考虑土与隧道的共同作用，通过迭代计算，获得隧道隆起变形。隧道变形计算分析简图如图3所示。

隧道变形预测计算方法为： 首先，通过式(1)和(2)计算开挖引起的隧道所在位置处土体的竖向变形ω1(x,y,z)； 其次，假设隧道不产生抗力，通过式(7)确定不考虑隧道抗力的隧道变形初始值s=ω1(x,y,z)-ω2(x,y,z)； 再次，通过式(5)计算该变形s下隧道的抗力F，并将各段矩形梁单元(隧道)处的抗力F代入式(3)的Pi中(Pi与Fi互为作用力和反作用力)； 从次，通过式(4)求得隧道抗力作用引起的土体变形ω2(x,y,z)； 最后，通过式(7)求出经过一次迭代得出的隧道变形值s。通过多次迭代，隧道变形量s将趋于稳定，该数值即为隧道实际隆起变形值。利用该隆起变形理论分析方法，通过参数分析，提出考虑不同卸荷比及土岩分界面埋深影响的起伏土岩地层中隧道最大隆起预测公式。

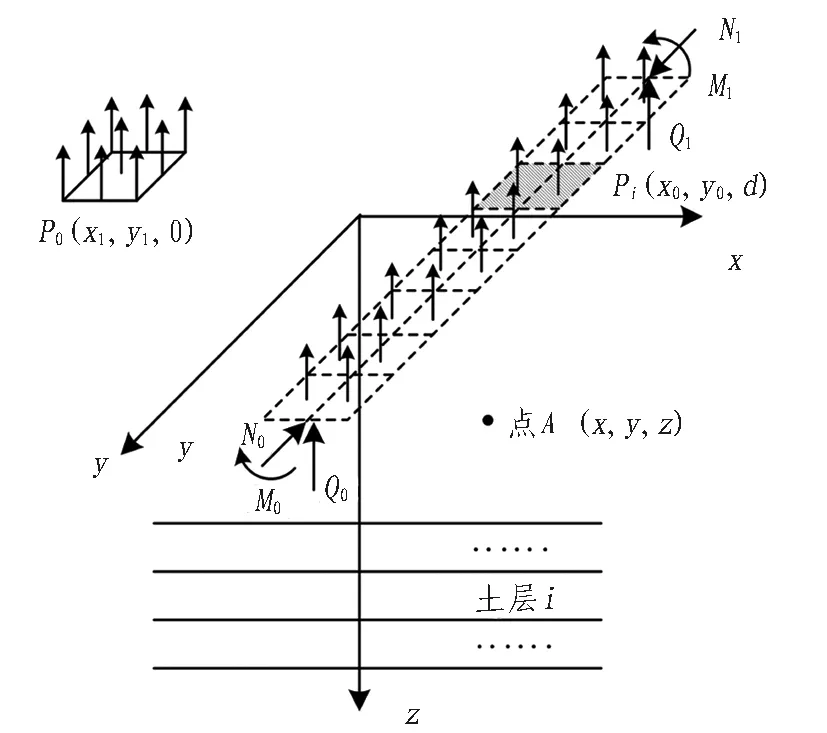
P0为基坑开挖卸荷量;Pi为梁单元i上的荷载；N0、N1分别为作用在隧道两端的轴力;Q0、Q1分别为作用在隧道两端的剪力；M0、M1分别为作用在隧道两端的弯矩。

图3隧道变形计算分析简图

Fig. 3 Schematic diagram of tunnel deformation calculation and analysis

2.1 计算方法

首先利用Boussinesq解计算基坑卸荷条件下土体内部任意点A的附加应力

(1)

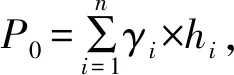
利用分层总和法计算基坑开挖卸荷引起的隧道处土体竖向变形

李碧华以女性特有的敏锐在小说中融入现代港人内心深处的香港意识，但其港人的身份在加剧这种意识的同时亦使得香港的本土意识在传统与现代两相对照中渐趋含混化了。

(2)

式中：Hi为基坑卸荷影响深度范围内隧道埋深以下的分层厚度，m；σi(x,y,z)为各分层中心处开挖卸荷引起的附加应力，kPa；Esi为各土层的压缩模量，kPa。

利用Mindlin解计算隧道抗力作用引起的附加应力，将隧道视为可沿隧道轴线分割成若干矩形单元的梁单元，隧道抗力引起的下卧土层中任意点处的附加应力为各矩形单元的作用力之和，可表示为：

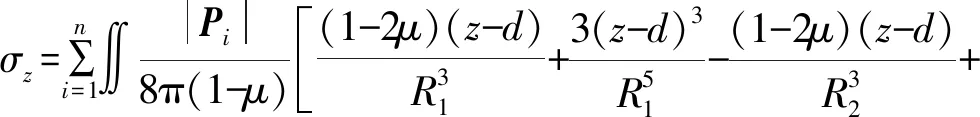
(3)

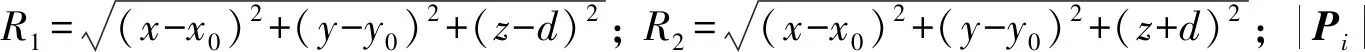
利用分层总和法求得隧道抗力作用引起的隧道处的土体竖向变形

(4)

由于隧道的横向尺寸远小于纵向尺寸，则可将隧道简化为图3所示的等效连续化地基梁模型，其受力如图3所示。当隧道足够长时，作用在隧道两端的轴力、剪力及弯矩可视为零，即N0=N1=0、Q0=Q1=0、M0=M1=0。对隧道弯曲变形进行分析，根据梁平衡方程则有：

K×s=F。

(5)

式中：s为隧道(连续梁)的位移向量，m；F为作用在隧道(连续梁)上的荷载，与隧道对土的抗力Pi互为作用力和反作用力，kPa;K为整个隧道(连续梁)的刚度矩阵，见式(6)。

(6)

考虑隧道与土的相互作用，由于基坑开挖过程中隧道与土体保持完全接触，即隧道与周围土体是变形协调的，据此进行耦合分析，可得位移协调方程：

s=ω1(x,y,z)-ω2(x,y,z)。

(7)

式中：s为经过n次迭代后的隧道位移向量，即为隧道隆起变形；ω1(x,y,z)为基坑卸荷引起的隧道处土体竖向变形，可由式(2)求得；ω2(x,y,z)为隧道抗力作用引起的隧道处土体竖向变形，可由式(4)求得。联合求解式(2)、(4)、(5)、(7)，经过迭代计算直至前后2次所得的计算结果误差不超过0.1%，即可求得隧道任意点处的隆起变形。

2.2 理论分析结果及经验预测公式

根据2.1节提出的隧道隆起变形分析方法，以残积土层与全强风化岩层交界面为分界线，分析分界线位置变化对下卧隧道隆起的影响规律，进而分析隧道位于岩层或土层中受上部基坑开挖卸荷的影响规律。本工程隧道埋深为20 m，定义分界线至地表高度为h，分别取h为0、5、10、15、20、25、30 m，模拟隧道与岩层、土层的相对关系。当h=0 m时，地表以下全部为岩层; 当h=20 m，隧道上方全部为土层。

为便于分析，设基坑开挖深度为He，隧道埋深为Hf，两者的比值定义为卸荷比R，即R=He/Hf。设基坑坑底距隧道拱顶之间的距离为ht，上部基坑卸荷跨度为B(隧道在基坑卸荷范围内的长度)。考虑到实际工程中主要关注隧道的最大隆起量，因此，本文只讨论开挖对隧道最大隆起量的影响。将隧道最大隆起量δ进行归一化处理，拟合曲线如图4所示。拟合出经验预测公式为：

(8)

(9)

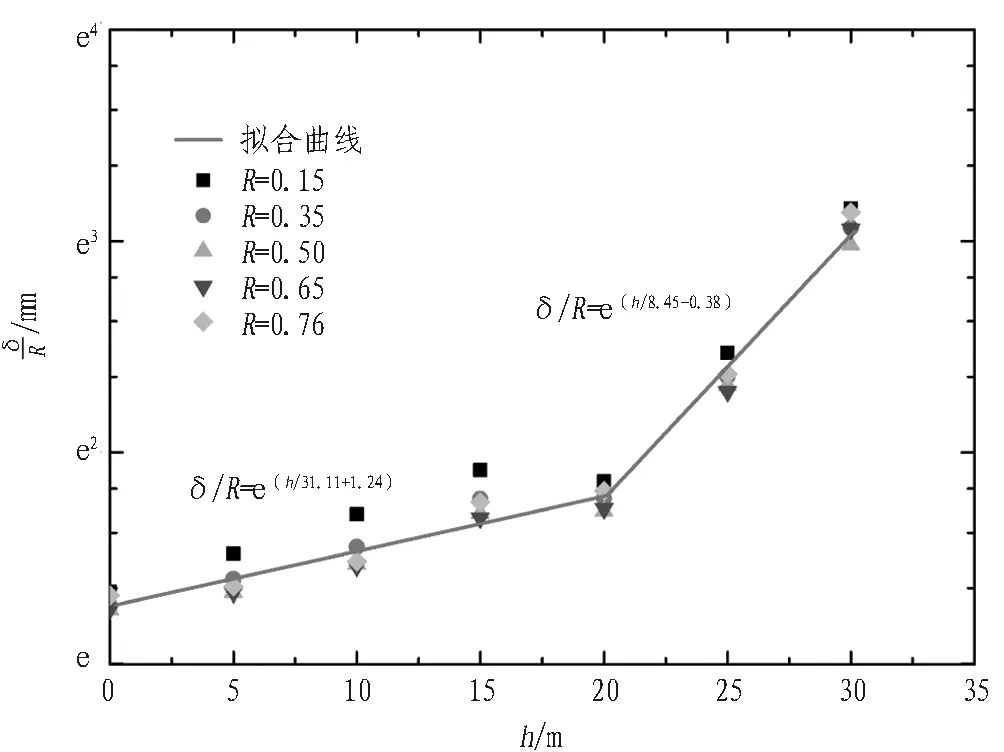
图4 隧道拱顶最大隆起量拟合曲线

Fig. 4 Fit curve of relationship between tunnel crown uplift deformation andh

由图4可知，上部开挖卸荷引起的下卧隧道竖向变形受隧道所处的地质环境影响显著。当h≤20 m时，隧道拱顶位于土岩分界面以下，隧道主体处于岩质土层中时，土层相对较硬，隧道竖向隆起随h增加的速率较慢，隧道隆起相对较小；当h>20 m(h=25 m和h=30 m)时，隧道拱顶位于土岩分界面以上，隧道主体逐渐向土层中转移，拱顶竖向隆起急剧增大。

3 人工与自动化监测结合的测试方案

由于厦门地铁1号线在基坑开挖过程中处于试运营期间，因此，采用人工监测结合自动化监测的方法进行监测，其中，自动化监测采用徕卡TM50全站仪。考虑到监测过程中地铁区间隧道内无通讯，因此，专门在隧道内架设光纤以保证监测工作的顺利开展。在初始状态调查过程中发现隧道存在渗漏水及裂缝。为了满足地铁保护要求，本次监测增加了裂缝及隧道衬砌内力监测，具体监测项目及监测频率见表2。区间隧道内测点布置如图1(a)所示。除人工道床竖向位移测点加密外，其他常规测项均为左右线各29个测点，其中，0.8倍的基坑开挖影响范围内按间距3 m布置，共23个测点； 0.8倍的基坑开挖影响范围外按5、8、12 m间距布置，共6个测点； 加密点在常规测项两端分别按9、10、10 m间距各加密3个测点。

表2 隧道监测项目及监测频率

4 既有隧道变形响应分析

4.1 理论预测与实测数据对比分析

针对以上工程案例，采用式(8)和(9)对施工过程中隧道的最大隆起量进行预测，预测结果如图5所示。对比分析预测结果与实测数据可知，实测数据位于预测曲线的两侧，且与拟合曲线接近。由此可知，所得到的经验公式可用于预测不同土岩分界面埋深下开挖引起的隧道隆起。

本工程左线和右线隧道在基坑中心处土岩分界面埋深分别为10 m和20 m，由式(8)可知，开挖过程中，δ/R的值分别为4.76 mm和7.29 mm。不同卸荷比下左线和右线隧道的最大隆起量实测值和预测值对比见表3。由表3可以看出，卸荷比较小时，理论预测结果与实测结果相差较大，随着开挖的进行，二者之间的误差逐渐减小，开挖结束后，实测值和预测值之间的误差小于3%，满足工程中的精度需求。

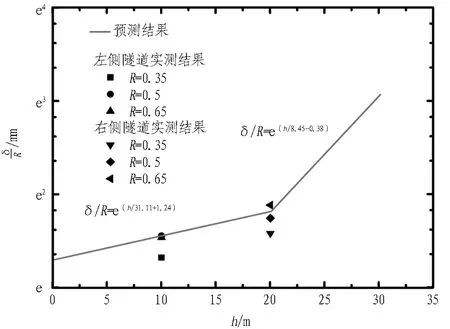
图5 隧道拱顶隆起量预测结果

Fig. 5 Prediction results and measured data of tunnel crown uplift deformation

表3不同卸荷比下左线和右线隧道的最大隆起量实测值和预测值对比

Table 3 Comparison between measured and theoretical values of maximum uplift deformation of left and right line tunnels under different unloading ratios

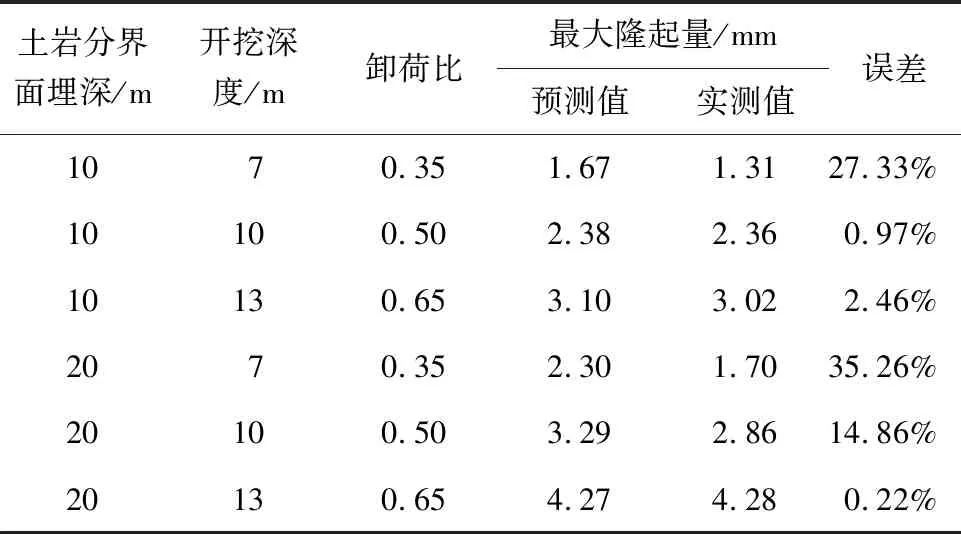
土岩分界面埋深/m开挖深度/m卸荷比最大隆起量/mm预测值实测值误差1070.351.671.31 27.33%10100.50 2.38 2.36 0.97%10130.65 3.10 3.02 2.46%2070.35 2.30 1.70 35.26%20100.50 3.29 2.86 14.86%20130.65 4.27 4.28 0.22%

基坑开挖引起的双线隧道竖向变形分布曲线如图6所示。开挖结束后到浇筑底板期间，隧道变形仍在不断增大，主要原因是底板施工期间经历强降雨，由于土体流变产生的时空效应，隧道变形不断增大； 浇筑底板后至隧道上方底板结构施工开始之时，左线拱顶最大变形约4.08 mm，增大约36%，右线隧道拱顶最大变形约6.65 mm，增大约58%； 随后进行结构施工，隧道受结构自重荷载作用下沉，至结构施工完成，左线隧道拱顶最大变形约3.4 mm，减小约20%，右线拱顶最大变形减小至5.4 mm，减小约20%。文献[11]和文献[14]的实测结果也表明，浇筑基坑底板能有效控制隧道的隆起。因此，施工中基坑开挖至底部时应尽快进行底板浇筑，避免长时间坑底暴露导致隧道竖向变形大幅增大。

4.2 地质条件对隧道最大隆起量的影响

为了进一步研究地质条件对隧道变形的影响，将左线和右线隧道最大隆起量和最大沉降量随时间的变化曲线进行对比分析，结果如图7所示。由图7可以看出，随着开挖的进行，右线隧道拱顶隆起以及沉降的最大值均大于左侧隧道。受地质条件起伏的影响，卸荷区域范围内，隧道左线大部分位于强、中风化岩层中，隧道右线大部分位于全风化岩及砂砾状强风化岩中，隧道左线比隧道右线地质条件好，同一时刻隧道右线相对于隧道左线拱顶竖向变形大，说明地质条件越好，隧道拱顶竖向变形越小。

土岩复合地层中，上部开挖引起的下卧隧道隆起变形规律明显不同于其他地质条件下的隧道隆起变形规律。郭鹏飞等[15]、Chen等[16]、黄宏伟等[2]和魏纲[12]收集了大量上跨基坑开挖隧道变形的实际工程监测数据。为了得到不同地质条件下上部开挖引起的下卧隧道的变形分布规律，对其进行整理，并与本文基坑数据进行对比。其中，除了梅溪湖隧道为矿山法隧道外，其他均为盾构法隧道。

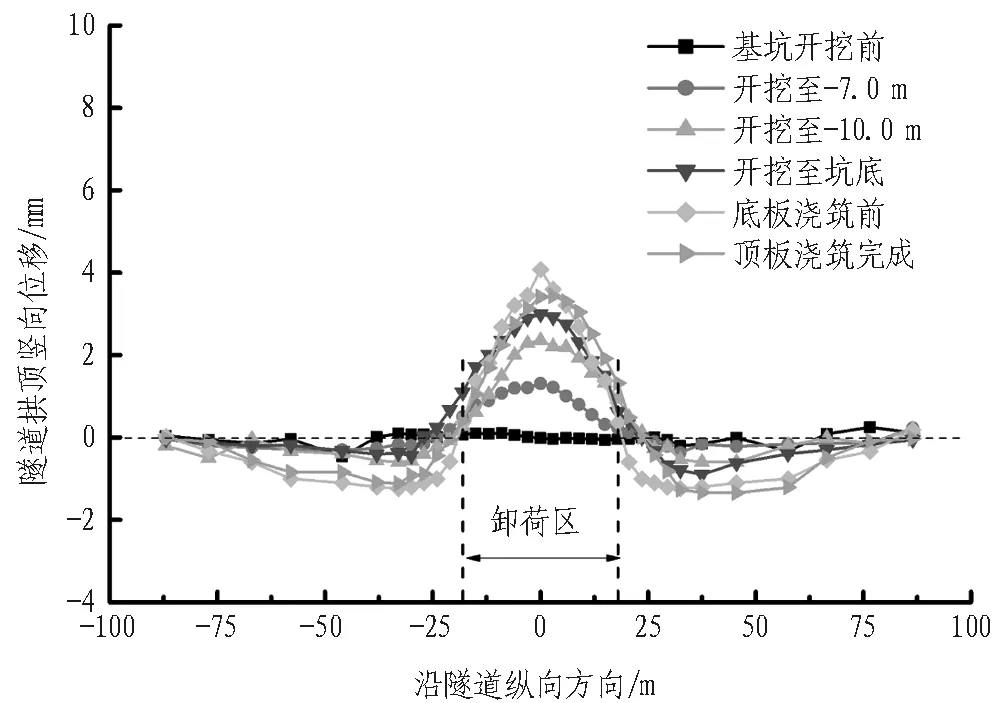
(a) 隧道左线

(b) 隧道右线

Fig. 6 Vertical cumulative deformation curves of tunnels caused by excavation of foundation pit

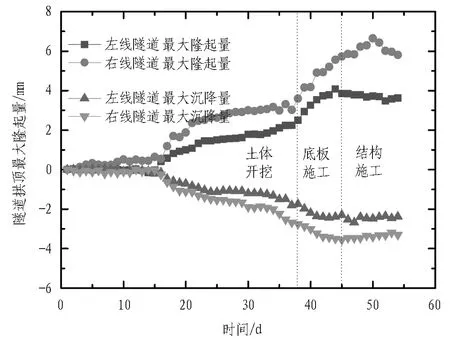
图7左、右线隧道拱顶最大隆起量与最大沉降量随时间的变化曲线

Fig. 7 Curves of maximum uplift deformation settlement of left and right line tunnel crown with time

不同地质条件下隧道最大竖向变形与开挖卸荷率R的关系如图8所示。由图8可知，不同地质条件下，隧道最大隆起变形总体上随上部基坑开挖卸荷率的增大而增大。不同地质条件下隧道最大隆起变形分布不同，软土地区隧道隆起变形较大，分布范围为9R～29R，平均15.5R；粉黏土地区隧道隆起变形次之，分布范围为5.77R～14R，平均11.2R；土岩复合地区隧道隆起变形最小，分布范围为0～5.77R，平均3.34R，同一卸荷率下为软土地区隧道隆起变形的1/5～1/4。本工程中基坑开挖到坑底时，隧道左右线的隆起变形分别为3.10 mm 和4.27 mm，在所统计的其他土岩地层上限附近。在基坑底板混凝土浇筑前，受降雨的影响，因土体流变效应隧道隆起变形进一步增大，左、右线分别增大了36%和58%，达到4.08 mm 和6.65 mm。

图8 隧道最大竖向变形与开挖卸荷率R的关系

Fig. 8 Relationship between maximum vertical deformation of tunnel and unloading rateR

5 结论与建议

本文针对厦门海沧海底隧道石鼓山立交段上跨地铁1号线区间隧道基坑开挖对下卧地铁隧道变形的影响问题，通过理论分析和现场测试，研究了土岩起伏地层对既有隧道在上部开挖卸荷下的变形响应影响，得出如下结论与建议。

1)提出基于Boussinesq解与Mindlin解的半解析预测方法，通过系统参数分析，得到考虑土岩界面位置变化的隧道最大隆起量预测公式。通过与现场实测数据进行对比，验证了所提出预测公式的准确性。

2)土岩起伏地层对既有隧道竖向变形的影响较大。测试结果显示，位于强、中风化岩中的左线隧道最大隆起变形约为3 mm，位于残积土及全风化岩中的右线隧道最大隆起变形约为4.2 mm。后续工程应加强位于残积土及全风化岩中隧道的保护措施。

3)风化岩层中既有隧道竖向最大隆起变形相对于软土地区隧道竖向最大隆起变形小。根据实测统计分析可知，软土地区隧道最大竖向隆起变形平均为15.5R(R为卸荷率)；风化岩地区隧道隆起变形较小，平均为3.34R，为软土地区隧道最大竖向隆起变形的1/5～1/4。本工程中基坑开挖引起的隧道隆起变形在所统计的其他土岩地层上限附近。

4)在基坑开挖到底至底板混凝土浇筑期间，受降雨的影响，左右线竖向隆起变形分别增大了36%和58%，分别达到4.08 mm 和6.65 mm。因此，降雨影响不可忽视，后续在残积土中开挖基坑应尽量减少坑底在暴雨中的暴露时间。