峡岛湍流海域水流力荷载计算方法探讨

刘建波 何超然 杨炎华 张磊 董海洋

摘要：与常规明渠流断面流速对数分布形态不同，外海连岛间海域断面流速呈现出复杂的分布特征，其主要原因在于凹凸不平海床面对海域流场分布有很大的影响。通过室内模型试验发现，峡岛湍流海域垂线流速基本呈二次抛物线分布形态，随后通过分析计算提出了以等效坡度为主因子的湍流流速分布公式。该公式计算结果与现场实测结果比较吻合，同时还给出了以抛物线分布形态为基准的水流力荷载计算修正系数。研究成果可为峡岛海域的工程结构设计提供参考。

关 键 词：水流力;修正系数;湍流流速;断面流速分布; 等效坡度;峡岛海域

中图法分类号： TV14 文献标志码： ADOI：10.16232/j.cnki.1001-4179.2019.01.033

与常规明渠流断面流速呈对数分布形态不同[1]，外海连岛间海域断面流速呈现出复杂的分布特征，其主要原因在于凹凸不平海床面对海域流场分布有很大的影响。国外相关学者通过试验对不同植被高度和种植密度下的底部植被对垂线流速分布规律及其参数的影响进行了研究，如Yokojima和Cassan等对植被明渠水流结构的影响进行了深入研究[2-3]。李冬等通过室内试验方法总结了断面流速分布与植被高度的关系[4]。槐文信等通过研究得出非淹没及淹没刚性植被稳恒流纵向流速垂向分布规律[5]。针对河/海床面形态对流场的影响，也有许多学者进行了相关研究。例如贾国珍等研究了底床上单个丁坝在完全淹没条件下的坝后水平流场及垂向流场[6]，给出了丁坝坝后流场的部分三维特性。李凤英等采用水槽试验[7]，研究分析了坡面径流水深、流速与流量、坡度的相关关系。已有的研究文献表明[8]，对于复杂、不规则海底的外海连岛海域，其断面流速形态不再符合常规明渠流流速分布特征。

浙江省舟山连岛工程作为我国东南沿海公路交通枢纽的重要组成部分，其建设面临着复杂多变的海洋环境[9]。该区域岛屿较为分散，岩层地质强度较高，连接各岛屿的通道大多采用桥梁工程。而外海岛屿间海域流速分布特征复杂，若采用常规对数分布形态确定水流荷载，可能会导致永久结构或临时结构的受力安全系数不足，这给桥梁工程（特别是基础工程）的设计和施工带来了极大的不确定性。基于上述原因，有必要针对外海连岛海域湍流流速分布规律进行深入研究。

1 室内水槽模型试验

1.1 底床模型设计

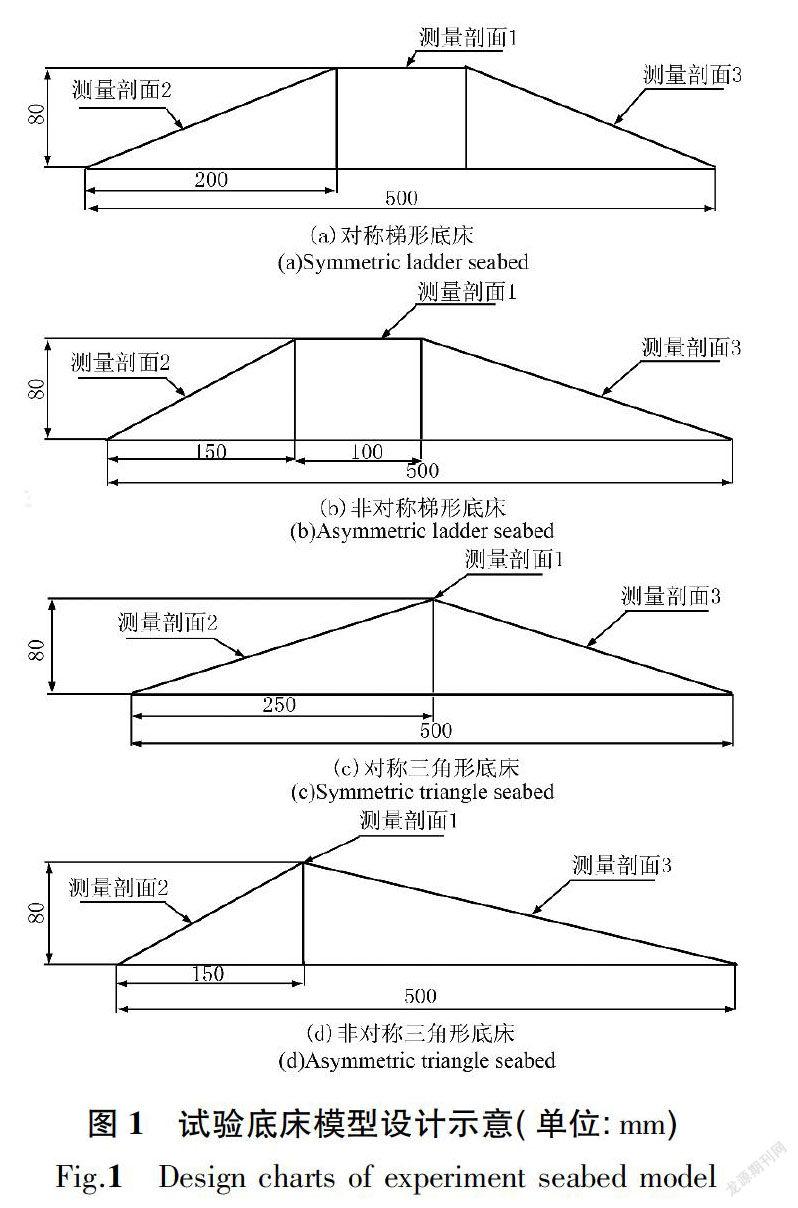
为了研究不同形状海床面对湍流流速（顺流向）分布形态的影响，在进行室内模型试验时，在水槽底设置了等腰梯形、不等腰梯形、等腰三角形和不等腰三角形等多种底床模型（见图1）。

等腰梯形迎水面坡度为0.4，不等腰梯形迎水面坡度分别为0.32（缓坡）和0.53（陡坡），等腰三角形迎水面坡度为0.32，不等腰三角形的迎水面坡度分别为0.23（缓坡）和0.53（陡坡），共4种不同坡度，如表1所示。

1.2 试验流量及工况

试验流量分别取60，50，40 L/s。试验中水深控制在30 cm，对试验中的水温进行实时测量，温度数值在19℃～22℃之間。在不同底床模型坡度（含无底床模型）、不同流量的情况下（共21种工况）进行流速观测。

2 湍流流速概率分析

湍流流速按以下公式计算：

U=u2+v2+w2（1）

式中，u、v、w分别为x、y、z方向上的平均流速，U为平均流速的大小。将平均流速进行数据整理和概率统计，计算其方差、标准差、均值等，并绘制其概率密度曲线。

2.1 无底床模型

在不放置凸底床模型的情况下，选用不同流速对水槽断面中间垂线的流速观测点时变情况进行分析，选取的测点距底面高度为h=0.3 H（9 cm）。图2为无底床模型不同流量情况下流速概率分布情况。

从图2可以看出，当流量Q=40L/s时，该观测点x轴流速均值0.194 8m/s，均方差为0.011 m/s;流量Q=50L/s时，该观测点x轴流速均值为0.281 9m/s，均方差为0.006 m/s;流量Q=60 L/s时，该观测点 x 轴流速均值为0.382 2 m/s，均方差为0.001 7 m/s。相对于流速均值，均方差较小，两者比值在10%以下，说明观测数值稳定，可以用于流速分布分析。

2.2 三角形底床模型

对于三角形底床模型，我们只选取了 Q =50 L/s工况下两种不同坡度的流速数据进行分析，如图3所示。

从图3可以看出，在 Q =50 L/s流量下，当 J = 0.23 时，流速均值为0.395 2m/s，标准差为0.001 m/s，流速为0.393 2～0.398 2 m/s，即均值上下3倍标准差 （ν±3σ）范围内出现的概率达到了92.17%;当J =0.32时，流速均值为0.385 4 m/s，标准差为0.005 5 m/s，流速在0.368 9～0.401 9 m/s，即均值上下3倍标准差 （ν±3σ） 范围内出现的概率达到了94.32%。

2.3 梯形底床模型

同样选取流量Q=50 L/s工况进行测试，见结果如图4所示。

从图4可以看出，在Q=50L/s流量下，当J= 0.40 时，流速均值为0.393 3m/s，标准差为0.002 4 m/s，流速在0.386 1～0.400 5 m/s之间，即均值上下3倍标准差（ν±3σ）范围内出现的概率达到了 93.72 %;当J=0.53时，流速均值为0.38m/s，标准差为0.005 2 m/s，流速在0.364 4～0.395 6 m/s之间，即均值上下3倍标准差（ν±3σ）范围内出现的概率达到了96.18%。

3 湍流流速分布特征

20世纪30年代，Keulegan等提出了明渠流速垂线分布呈对数分布形式[10]：

u+=Alny++B（2）

式中，u+=u/u*，y+=yu*/ν，u*为摩阻流速，ν为运动黏度，A、B为常数。其中A=2.3/κ，κ为Karman常数，B为反映壁面情况的积分常数[11-12]。

为了验证上述明渠流垂线分布公式在湍流流速中的适应性，对等腰三角形底床不同流量下垂线流速分布形态与理论对数分布曲线进行了对比。

从图5中可以看出，该试验条件下，对于高度 h=（0.2～0.3）H段，对数流速分布和实测数据吻合较好，而在（0.4～0.7）H段，实测流速达到垂线上的最大区域，实测流速大于对数分布规律理论值;当高度高于0.7 H以上时，接近水体表面处流速减小，小于对數分布曲线得到的流速理论值。对数流速分布规律是基于底面摩阻而建立的[13]，体现了水体底床摩阻对于水流的影响，所以对水底0.2 H 以内的流速分布描述较为准确，而对于深水急流海峡来说，底面摩阻作用范围相对较小，大部分水体的流速垂线分布与对数分布规律偏差较大。对于不同的断面流量试验，均观察到类似现象，说明对数流速规律对深水急流海峡垂线流速分布上存在一定的偏差，尤其对于水体表层和中段，对数流速分布规律并不能准确地描述流速分布。

4 峡岛湍流流速垂向分布公式

借鉴上述研究，采用二次抛物线拟合流速的垂线分布情况[14-16]。为得到更普遍规律，笔者首先将流速无量纲化，其无量纲水深的关系可以用二次抛物线描述：

uv=a（ yH）2+b（ yH）+c（3）

式中，u为测线上任一点流速，v为断面平均流速，y为测点距海床底距离，H为水深，a，b，c为待定系数。

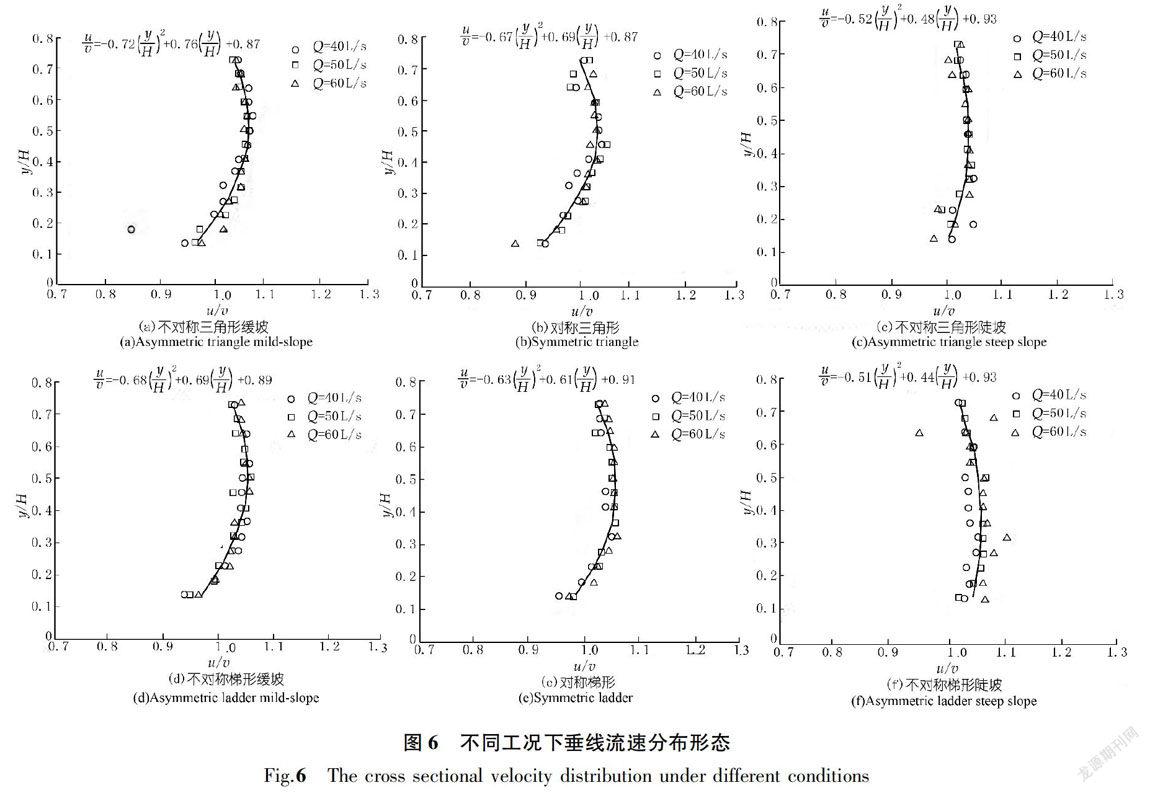
无量纲流速和水深试验数据的二次抛物线表示结果如图6所示。

从图6可以看出，不同工况下抛物线拟合效果较好，相关系数大多在0.90以上，只有图6（f）有若干个测量离散比较大的点，但其均匀地分布在拟合曲线的两侧，属于正常的测量误差。这里用断面平均流速代替摩阻流速作为无量纲流速的分母，是因为凸底处的水流不再是均匀流，其摩阻流速难以确定[17]，而断面平均流速容易确定，这样处理便于公式的应用。

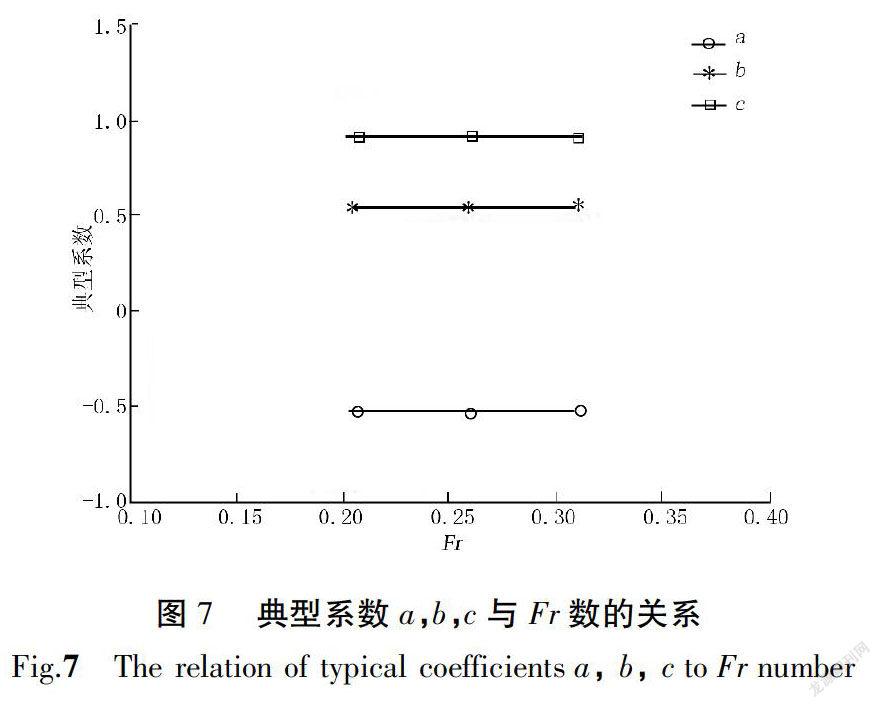
尽管各组试验流速垂向分布的规律相同，但相关系数a，b，c却各不相同。笔者从水流强度因子Fr数和凸底迎水坡度两方面对其进行了分析[14]，结果如图7所示。

统计分析水槽试验结果，发现典型系数a，b，c与水流强度因子Fr数基本无关，拟合系数随弗劳德数Fr的变化曲线基本为一条直线，故系数a，b，c主要受凸底迎水坡度影响。

分析本次试验的变量可知，a，b，c的大小与来流速度和凸底迎水坡度有关。前面已指出，在相同的凸底下，a，b，c受来流速度的影响并不大，不同的凸底坡度不一样，a，b，c取值也有较大差异。将本文中以公式（1）拟合得到的a，b，c与坡度放在一起，如表2所示。

从表2中可以看出，不论是三角形凸底，还是梯形凸底，随着坡度的增加，a，c的值逐渐增加，b的值逐渐减小。将a，b，c的值和坡度J的关系用曲线拟合，相关系数均在0.95以上，拟合曲线如图8所示。

图8 a，b，c系数与坡度J的关系  Fig.8 The relation of coefficients  a， b， c  to seabed slope  J

从图8可以看出，不论对于三角形凸底还是梯形凸底床，系数a，b，c数值上与断面流速（即Fr）无关，和凸底床坡度J表现为线性相关关系。通过线性拟合，可以总结得到系数与坡度的相关关系如下：

a=1.27J-1.11（4）

b=-1.78J+1.30（5）

c=0.29J+0.78（6）

将式（4）～（6）代入式（3）中，得到如下关系：

uv=（1.27J-1.11）yH2+ （-1.78J+1.30）yH+0.29J+0.78（7）

5 公式误差分析

为了分析上述流速垂向分布公式的误差，在实验室内又对0.229，0.293和0.360等3种不同等效坡度下计算流速和实测流速进行了对比验证，验证结果见图9。

从图9可以看出，在整个流速范围内（0.2～0.5 m/s），几乎所有流速计算值均匀地分布在理论曲线的两侧，相对误差在8%以内。因此，可以说明提出的公式能很好地反映实际流速分布规律，少数测点相对误差大于8%，属于正常的偶然误差。当流速在0.28 m/s 以下时，测点流速更为集中在理论曲线两侧，计算值偏离理论曲线更小，表明流速较低的情况下，公式的精度更高。

6 分布形态现场验证

为了验证流速分布规律的合理性，课题组在秀山大桥项目现场对断面流速进行了实测[18]。图10为现场实测数据与计算得到该点垂线流速分布的对照。

从现场验证的结果来看，垂线实测涨落潮流速分布较为符合试验得到的凸底床垂线流速分布规律。对于涨潮流，偏差较大的数据点集中于距床底高（0.3～0.5）H（垂线中下部）处，而对于落潮流阶段，偏差较大的数据点位于（0.5～0.8）H（垂线中上部）处;水体中上层流速较大，流速最大的点集中于（0.6～0.9）H之间，而（0.2～0.5）H（垂线下部）段流速梯度较大，流速沿水深方向降低较为剧烈，上下层水体交换较强，紊动强烈;高度0.5 H以上，垂线流速较大而流速梯度不大，水流对桥墩的作用力主要表现为正应力，高度0.5 H以下，垂线流速较小而流速梯度较大，水流对桥墩的作用力主要表现为切应力。

7 水流力计算

现有的规范公式中[19]，水流力按（8）式计算：

F= 12Cdρv2A（8）

式中，Cd为阻力系数，ρ为水的密度，v为水流断面平均流速，A为桩柱垂直于水流方向的投影面积。在深水急流海峡中，因为底床坡度的变化，导致水流纵向流速重新分布，下层水体流速偏大，所以与该规范公式相比，水流力的数值和分布规律也会发生改变。

水流力大小为

F=∫ 12Cdρu2（z）dA（9）

式中，u（z）为海峡流速沿水深方向的分布函数，根据上文分析，对于存在凸起底床的情况，流速垂线分布函数可以用二次抛物线的形式表示。假定桩径D=2m，水深即桩柱高度H=20m，断面平均流速v=2.3m/s，取海水密度ρ=1.25×103kg/m3，图11为抛物线计算水流力（F2）与规范公式计算水流力（F1）之比（F2/F1）随坡度的变化曲线。

从图11可以看出，随着坡度的增大，F2/F1比值呈现逐渐增大的规律。因此，为了更方便计算凸底床水流力的数值，引入系数ζ，优化后的水流力公式为

F= 12Cdζρv2A（10）

其中， ζ为修正系数，ζ= ∫u2（z）dAν2A ，体现了凸底床条件下流速重新分布导致的水流力增大效果。根据上文中的抛物线流速分布公式

u（z）ν=azH2+bzH+c（11）

可计算得到：

ζ= 15a2+ 13b2+ 12ab+ 23ac+bc（12）

结合上文中坡度与抛物线流速分布系数a、b、c的关系式，得到系数与迎水面坡度的关系：

ζ=-0.124J2+0.244J+1.004（13）

从以上计算和分析中可以知道：在底床坡度较小的海峽条件下，其水流力与规范值相近，而当迎水面坡度较大的情况下，水流力计算值超过规范值较多，且该比值随着坡度的增大而增大。施工过程中，当桩柱底床存在凸起，桩基建立在凸起床面上时，可以利用以上修正系数对桩柱受到水流力数值进行重新计算。

8 结 论

采用理论推导、试验模拟和现场验证相结合的方法，对峡岛海域内湍流流速垂线分布形态进行了研究，主要结论如下。

（1） 研究发现峡岛海域流速分布形态并不符合常规明渠流对数分布特征，而是服从二次抛物分布规律，主要是由于峡岛海域凹凸不平的海床地形造成的。

（2） 总结提出了以等效坡度为主因子的峡岛海域流速垂线分布公式。研究表明随着海底床坡度的增大，其最大流速位置逐渐下移，这与常规明渠流最大流速位置发生在表层是有很大差别的。

（3） 由于分布形态的不同，由抛物线形态计算的水流力要大于规范（对数分布）计算的水流力，且随着坡度增大，两者的比值也会逐渐增大。本文研究发现，两者比值的增大幅值与海床底的坡度也存在一定的关系。关于这点，在今后类似峡岛海域下结构设计时应引起重视。

参考文献：

[1]胡春宏，倪晋仁.矩形明槽中断面紊流流速分布规律的初步研究[J].水利水运科学研究，1988，（2）：27-36.

[2]Yokojima S，Kawahara Y，Yamamoto T. Impacts of vegetation configuration on flow structure and resistance in a rectangular open channel[J].Journal of Hydro-environment Research，2015，9（3）：295-303.

[3]Cassan L，Belaud G，Baume J P.Velocity profiles in a real vegetated channel[J].Environmental Fluid Mechanics，2015，15（6）：1263-1279.

[4]李冬，胡旭跃，刘斌.有植被明渠垂向流速分布特性的试验与研究[J].水道港口， 2007，28（03）：178-182.

[5]槐文，信磊，李丹，等 有植被明渠纵向流速垂向分布特性的PIV试验分析[J].实验流体力学，2009，23（1）：26-30.

[6]贾国珍，佘俊华，王涛，等.淹没丁坝坝后水流结构PIV试验研究[J].水电能源科学，2012，30（3）：84-86.

[7]李凤英，李琳，何小武.坡面流水力学参数的估算[J].江西农业大学学报，2006，28（3）：477-480.

[8]孙志林，董海洋，李霖生.深水急流海峡湍流流速分布研究[C]∥第十八届中国海洋（岸）工程学术讨论会论文集，2017.

[9]丁琦.舟山群岛峡道海区潮流切变锋特性的二维数值研究[D].杭州：浙江大学，2008.

[10]Keulegan G H.Laws of turbulent flow in open Channels[J].Journal of Research of the National Bureau of Standards，1938，21（6）：707-741.

[11]付辉，杨开林，王涛，等.对数型流速分布公式的参数敏感性及取值[J].水利学报，2013（4）：489-494.

[12]张鑫.明渠紊流流速分布公式的对比和研究[D].南京：河海大学， 2008.

[13]刘春晶，王兴奎，曹文洪，等.明渠均匀流流速分布的指数、对数公式对[C]∥中国水利学会青年科技论坛论文集，2005.

[14]宋光春，钟秋友.明渠流速分布经验公式及其在高洪测流中的应用[J].武汉大学学报：工学版，1992（4）：393-400.

[15]孫东坡，王二平，董志慧，等.矩形断面明渠流速分布的研究及应用[J].水动力学研究与进展，2004，19（2）：144-151.

[16]罗佳.圆形断面管道无压均匀流水力特性研究[D].北京：清华大学，2016.

[17]刘春晶，李丹勋，王兴奎.明渠均匀流的摩阻流速及流速分布[J].水利学报，2005，36（8）：950-955.

[18]JTS 144-1-2010 港口工程荷载规范[S].北京：人民交通出版社，2010.

引用本文：刘建波，何超然，杨炎华，张 磊，董海洋.峡岛湍流海域水流力荷载计算方法探讨[J].人民长江，2019，50（1）：184-190.

Discussion on calculation method of turbulent flow forceload in sea area of channel island

LIU Jianbo1， HE Chaoran1， YANG Yanhua1， ZHANG Lei1， DONG Haiyang2

（1. CCCC Second Harbor Engineering Co.， Ltd.， National Technology Center， Wuhan 430040， China; 2. Ocean College， Zhejiang University， Hangzhou 310058， China）

Abstract：In contrast to the logarithmic distribution of the flow velocity in the open channel section， the cross-section velocity in sea area of channel island presents complex distribution characteristics because the uneven sea bed has a great influence on the distribution of the flow field in the sea area. Through the indoor model test， it was found that the vertical velocity in the turbulent sea area of the channel island was in the form of a quadratic parabola， and then through the analysis and calculation， the turbulence velocity distribution formula was put forward， which takes the equivalent slope as the main factor. The calculation results of the formula were in good agreement with the field measured results， and the correction coefficient of the flow load calculation based on the parabola distribution pattern was also given. The study can be used as a reference for the engineering structure design in the sea area of channel island.

Key words： flow force; correction coefficient; velocity of turbulent flow; velocity distribution in section; equivalent slope; sea area of isthmus island