基于随机波动模型（SV）的人民币汇率风险预测

孟庆斌 宋烜 宋祉健

【摘要】人民币汇率风险的精准计算和预测是管理和控制汇率风险的首要条件，并随着外汇市场的发展与完善受到越来越多的重视。在此背景下，利用随机波动模型和在险价值模型对汇改后的人民币汇率风险进行度量与预测。首先，基于贝叶斯估计方法，运用四种随机波动模型对人民币汇率波动进行拟合，并运用DIC准则筛选出拟合效果最好的SV-N模型；然后，利用筛选出的模型结合在险价值模型对人民币汇率风险进行度量；最后，基于所构建的SV-N-CVaR模型，对所选样本范围之外100日的人民币汇率风险进行一步向前预测。将预测值与真实值进行比较，可以看到预测正确率为87%，汇率风险预测值和真实值的变动趋势基本相同，说明风险预测模型与真实状况保持了较高的一致性，在所构建模型的基础上建立人民币汇率风险预测体系是可行的。

【关键词】人民币汇率；风险预测；随机波动模型；在险价值模型

【中图分类号】F830【文献标识码】A【文章编号】1004-0994（2019）24-0151-7

【基金项目】国家自然科学基金面上项目“卖空机制、私有信息与知情交易”（项目编号：71772174）；国家自然科学基金青年项目“政府监管、市场监督与公司信用债券定价”（项目编号：71302156）；中国人民大学面上项目“揭开价格发现的‘黑箱——市场价格发现模型与实证技术研究”（项目编号：2017030185）

一、引言

外汇市场是每个国家金融市场的核心组成部分，汇率稳定对宏观经济稳定至关重要。尤其是对于新兴市场国家而言，短时间内的汇率大幅波动会对金融市场，甚至整个国家的宏观经济产生严重的后果。2015年之前，由于人民银行对我国汇率波动幅度管制较严，因此汇率风险相对较小。2015年的“8.11汇改”为我国人民币国际化与市场化进程起到了积极的推动作用，但此后匯率波动上限大幅提高，汇率风险也随之上升。十九大报告首次提出的“宏观审慎政策”和央行行长首次警示的“明斯基时刻”说明我国对金融风险的重视程度不断提高。在这样的背景下，汇率风险作为金融风险的一部分，迅速成为上至国家决策层下至金融市场关注的焦点问题之一，也引起了学术界的广泛讨论。

科学管控汇率风险的基础和前提是对汇率风险进行准确的度量和预测，对此学者们进行了大量的研究。如惠晓峰等[1]运用GARCH模型对1994年汇改后的人民币汇率波动进行刻画，并对汇率进行了一步向前的预测。王雪等[2]运用多元GARCH模型（GARCH-BEKK）测算了我国汇率的波动，并将测算结果运用于我国的出口贸易中。张海波等[3]运用GARCH模型刻画了我国汇率波动，并结合在险价值（VaR）模型测算了人民币汇率风险。GARCH模型将金融时间序列的条件方差表示为残差平方和条件方差的滞后项的线性组合，较好地反映了汇率波动中的时间聚集效应。然而，现实中汇率等金融时间序列的波动率变化更接近于一般随机过程，波动率具有时变性，但GARCH族模型却不能较好地刻画这一特点，这就影响了它的拟合度和预测精度。随机波动（SV）模型考虑了波动率的时变性，很好地弥补了GARCH族模型的不足，从而有利于提高刻画的准确性[4-6]。实际上到目前为止，SV模型已经在金融研究，尤其是对股票市场[7-9]、期货市场[10-12]、债券市场[13]的研究上得到了比较广泛的应用。然而，由于汇率的影响因素更加复杂，且我国汇率受政策干预程度较高，到目前为止，只有少数学者将SV模型引入我国汇率或汇率风险的刻画，鲜有学者将其运用于我国汇率风险的预测中[14-16]。

为此，本文尝试利用SV模型对我国汇率风险进行刻画，在此基础上还将对汇率风险进行样本外预测，从而为国家政策制定者科学管控汇率风险提供理论依据。首先，运用四种随机波动模型（SV-N、SV-T、SV-MN和SV-MT）对人民币汇率波动进行拟合，并运用DIC准则筛选出拟合效果最好的模型；然后，利用筛选出的模型结合在险价值模型（VaR和CVaR）对人民币汇率风险进行度量；最后，在度量人民币汇率风险的基础上，对人民币汇率进行一步向前预测。研究发现，在本文所考察的SV模型中，SV-N模型对汇率波动的拟合效果相对最优，且当运用于人民币汇率风险刻画和预测时，SV-N模型也取得了很好的效果。

本文的理论贡献体现在两个方面：①使用随机波动模型对包括重大外生政策冲击——“8.11汇改”在内的时间区间中的人民币汇率风险进行刻画和度量，与之前文献广泛使用的GARCH族模型相比，更好地拟合了汇率的波动特征，提高了汇率风险的度量精度。在此基础上，构建了人民币汇率风险的样本外预测模型，且取得了令人满意的结果。②由于本文建立的人民币汇率风险刻画和预测模型对外生政策冲击有较好的包容性，因此该结果可为政策制定者和外汇市场参与者更加准确地度量与预测我国汇率风险提供借鉴，从而科学地制订风险管控和预警方案。

二、基于随机波动模型的在险价值模型

1.在险价值模型。J. P. Morgan公司1994年首次提出在险价值（Value at Risk，简称VaR）的概念，其数学表达式为：

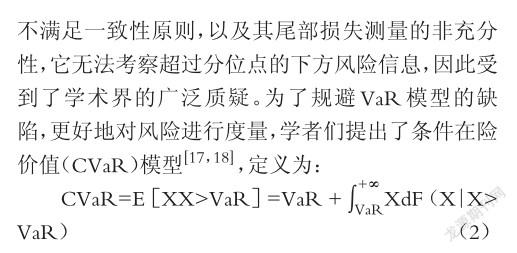
由此可见，CVaR模型反映了在一定的置信水平下，投资组合超过潜在最大损失的平均潜在损失。同时，CVaR的运算以VaR为依托，且在CVaR的运算中能够同时得出二者的值。

CVaR具有包括时移不变性、劣可加性、正齐次性及单调性在内的一致性，与不具有这一性质的VaR相比精度更高、适用范围更广[19]。将CVaR运用于人民币汇率风险的度量与预测时，反映了在一定的置信水平下，人民币汇率风险超过潜在最大损失的平均潜在损失，因此能够更好地对我国汇率进行度量。

2.随机波动模型。从上文可以看到，计算在险价值模型的核心为准确地估计汇率波动率σt。然而如前所述，现实中汇率等金融时间序列波动的变化更接近于一般随机过程，波动率具有时变性，但GARCH族模型却不能较好地反映该特点，这就影响了拟合度和预测精度。为此，本文利用善于捕捉波动率时变性的随机波动（SV）模型对其进行拟合。同时为了提高拟合精度，分别使用SV-N、SV-T、SV-MN和SV-MT模型对人民币汇率波动进行刻画，并对各模型结果进行比较。

從表1可以看到，人民币汇率变动存在明显的右偏（偏度为1.83>0）特征，且峰度较高（峰度为16.63>3），同时其JB统计量为4151，说明该序列与正态分布相去甚远，具有典型的尖峰厚尾特征。由ADF统计量可知，人民币汇率变动序列是平稳的，为后续利用SV族模型进行建模创造了条件。

2.基于SV模型的人民币汇率波动性分析。针对人民币兑美元汇率，本文利用MCMC方法对SV-N、SV-T、SV-MN、SV-MT四个模型中的未定参数进行贝叶斯估计，各模型参数估计结果见表2。

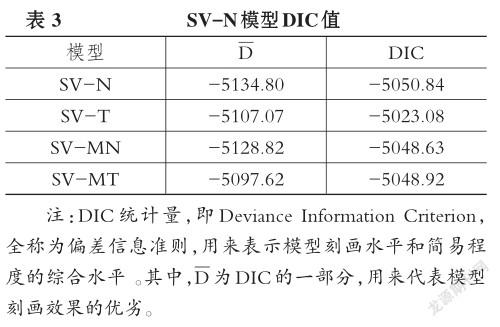
为了从四个模型中筛选拟合效果最好的模型，本文选用目前常用的DIC准则，结果见表3。在DIC准则中，D表示模型的刻画水平，具体而言，D值较低的模型对样本数据的刻画效果较好；PD代表模型自身的简易程度，PD值较大的模型自身的简易程度较差。所以，DIC值越大，模型的刻画水平越差、简易程度越差，模型更应该被淘汰，反之，则更应该被保留。从表3可以看到，SV-N模型的DIC值最小，说明其对人民币汇率的拟合效果最优，因此本文选用SV-N模型，即表2中的式（20）来进行人民币风险测度和预测。

SV-N模型中各未定参数的后验分布密度如图1所示。由图1可以看出，各未定参数的分布较为集中，也证明本文的估计结果是可靠的。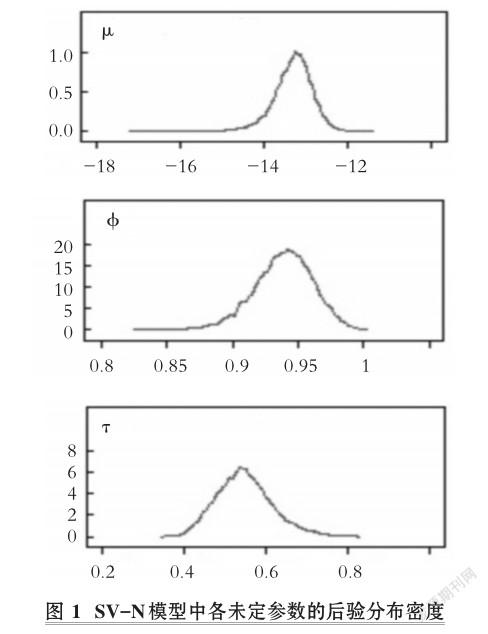

由以上的贝叶斯估计结果可以得出如下结论：

（1）人民币汇率的对数波动（μ）的均值为-13.3193，α=0.05时的置信区间是[-14.4000，-12.4975]，结果显示样本序列的对数波动数值较大，说明人民币汇率的波动率较高。

（2）当期波动对远期作用持久性（？）的均值为0.9388，α=0.05时的置信区间为[0.8913，0.9792]，说明汇率的波动对外汇市场远期的作用是持久的。

（3）汇率的对数波动方差（τ）的均值为0.5474，在显著性水平α=0.05时的置信区间为[0.4259，0.6991]，数值相对较小，说明刻画人民币汇率的对数波动的模型较好。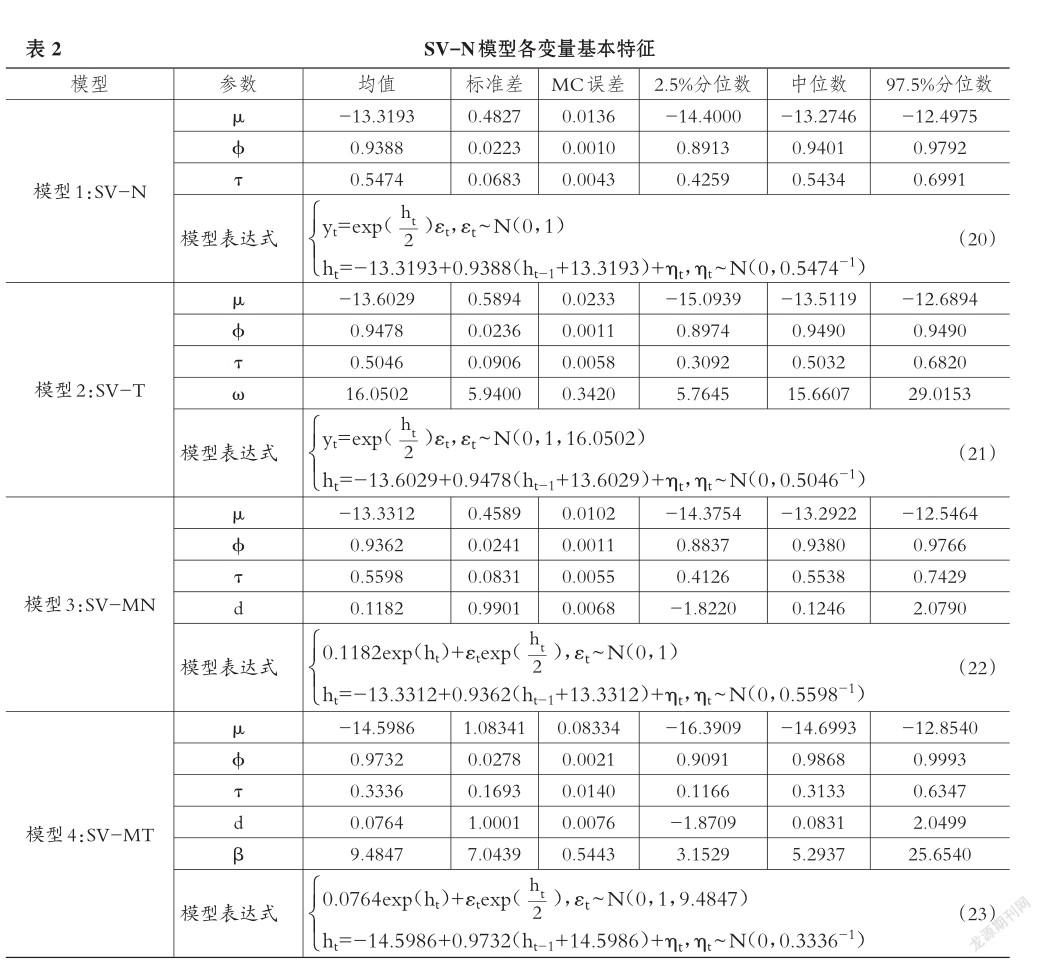

3.人民币汇率风险的度量。在上文所得到的人

民币汇率对数波动率（ht）的基础上，本文进一步利用式（5）对人民币汇率风险（CVaR）进行度量，结果见表4。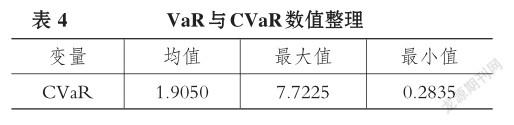

为验证SV-N-CVaR模型的适用性，本文采用Kupiec检验法对其进行考察。为此，本文首先对汇率序列作差，得到汇率变动序列{△pt=pt-pt-1|t=1，2，…，500}；在此基础上，定义似然比率（Likelihood Ratio）统计量为：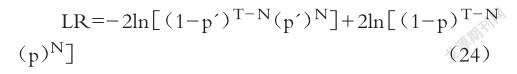

其中，T为样本量，N为CVaR小于汇率变动量的次数。因此p=N/T即为CVaR小于真实差值的频率。而当CVaR的置信水平为c时，CVaR小于汇率变动量的期望频率则为p=1-c。

计算可得，LR统计量为3.89，接近于5%的显著性水平下的阈值（3.84），因此本文风险度量的结果是可以接受的。考虑到本文样本区间涵盖了2015年“8.11汇改”时段，Kupiec检验的结果说明本文的风险度量在外生政策冲击下具有稳健性，能够全面考察人民币汇率风险。

4.人民币汇率风险预测。为了考察本文所构建的SV-N-CVaR的预测效果，本文对2017年5月23日到2017年10月19日，即上文所选样本范围之外100日的汇率风险进行一步向前预测。在对每日汇率风险进行预测时，均从该日的上一个交易日开始，向前取500个有效的人民币汇率中间价作为训练集，用以计算SV-N模型中的未定参数。将其代入式（20）和式（5），计算该日的汇率风险，并与当日真实风险进行比较。以预测2017年5月25日的汇率风险为例，训练集选为2015年5月6日至2017年5月24日，共500个汇率数据。具体预测结果见图2。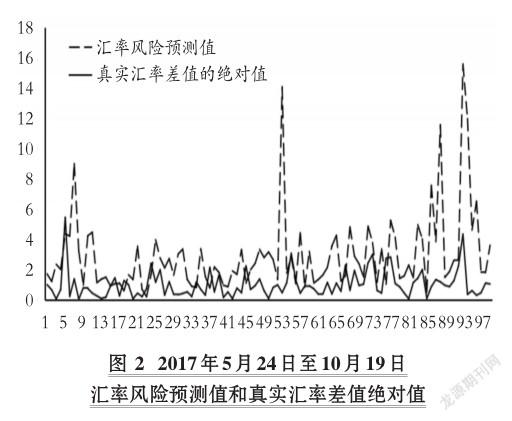

结果表明，在100次预测中，有87次的预测值大于真实差值，预测正确率为87%，结果是可以接受的。从图2也可以看到，汇率风险预测值和真实值的变动趋势基本相同，说明外汇风险预测值与真实状况保持了较高的一致性，本文所构建的SV-N-CVaR模型预测效果较好。

四、结论

本文利用SV模型建立了汇率风险度量模型，并以此为基础对我国汇率风险进行了样本外预测。为此，首先运用四种随机波动模型（SV-N、SV-T、SV-MN和SV-MT）对人民币汇率波动进行拟合，并运用DIC准则进行了模型筛选；然后，利用筛选出的模型结合在险价值模型（VaR和CVaR）对人民币汇率风险进行度量；最后对人民币汇率进行了样本外预测。研究发现，相对于其他模型，SV-N模型能够更精确地拟合人民币汇率波动趋势，基于该模型建立的SV-N-CVaR模型对人民币汇率风险的预测准确性更高，且对样本外的汇率风险的预测效果令人满意。

结合本文的研究可以得到如下启示：实现人民币国际化有利于解决我国的货币错配问题，提高人民币的国际定价能力。然而，在人民币国际化进程中，汇率波动引发的问题越来越多，随之而来的汇率风险可能对我国金融体系甚至經济安全带来挑战。尤其是我国正处于经济发展的转型换挡期，汇率风险失控有可能上升和转化为实体经济的系统性风险。人民币汇率形成机制改革应结合国际经济发展趋势以及我国自身经济发展状况循序渐进，既不能盲目追求市场化而忽视风险，也不能为了方便管控而固步自封。应该在保证风险可控的范围之内，稳步推进人民币国际化进程。同时应在人民币国际化逐步推进的过程中，对汇率风险保持高度警惕，建立有效的汇率风险防范体系和预案，当风险过大时，适度放缓国际化进程甚至以退为进亦不失为明智之举。

具体到风险模型的构建上，从本文的研究可以发现，基于传统的时不变模型所构建的汇率风险度量和预测模型适用性有限，尤其是在面对如“8.11汇改”这种外生事件的情况下，效果更差。而本文利用考虑波动率时变的SV-N所建立的汇率风险度量模型则能够对我国汇率风险进行较为准确的度量，并对样本外的风险进行较好的预测。因此，结合我国国情和汇率形成机制，利用近年来计量经济学模型的最新成果，继续构建和完善汇率风险度量和预测模型是我们未来探索的方向。

主要参考文献：

[1]惠晓峰，柳鸿生，胡伟何等.基于时间序列GARCH模型的人民币汇率预测[J].金融研究，2003（5）：99～105.

[2]王雪，胡未名，杨海生.汇率波动与我国双边出口贸易：存在第三国汇率效应吗[J].金融研究，2016（7）：1～16.

[3]张海波，陈红.人民币汇率风险度量研究——基于不同持有期的VaR分析[J].宏观经济研究，2012（12）：25～31.

[4]Jacquier E.，Polson N.，Rossi P. Bayesian Analysis of Stochastic Volatility Models[J].Journal of Business & Economic Statistics，1994（4）：371～417

[5] Danielsson J. Multivariate Stochastic Volatility Models：EstimationandaComparisonwith VGARCH Models[J].Journal of Empirical Fi？ nance，1998（2）：155～173.

[6]余素红，张世英，宋军.基于GARCH模型和SV模型的VaR比较[J].管理科学学报，2014（5）：61～66.

[7]王春峰，蒋祥林，李刚.基于随机波动性模型的中国股市波动性估计[J].管理科学学报，2003（4）：63～72.

[8]吴鑫育，马超群，汪寿阳.随机波动率模型的参数估计及对中国股市的实证[J].系统工程理论与实践，2014（1）：35～44.

[9]吴鑫育，李心丹，马超群.门限已实现随机波动率模型及其实证研究[J].中国管理科学，2017（3）：10～19.

[10]刘庆富，华仁海.重大风险事件对中国商品期货市场的冲击效应——基于学生分布的随机波动模型[J].数量经济技术经济研究，2012（5）：89～103.

[11]谢赤，杨妓妓，赵亦军.基于SV-M-POT-PSRM模型的期货维持保证金水平设定——关于沪深300股指期货高频数据的实证分析[J].系统管理学报，2013（6）：768～776.

[12]秦学志，郭明，宋宇.基于SV-POT-TDRM的沪深300股指期货尾部风险研究[J].系统管理学报，2017（5）：888～896.

[13]刘善存，牛伟宁，周荣喜.基于SV模型的我国债券信用价差动态过程研究[J].管理科学学报，2014（3）：37～48.

[14]杨爱军，蒋学军，林金官等.基于MCMC方法的金融贝叶斯半参数随机波动模型研究[J].数理统计与管理，2016（5）：817～825.

[15]何启志.新常态背景下汇率市场化改革与汇率波动性研究[J].国际金融研究，2017（3）：67～76.

[16]刘祥东，范彬，杨易铭等.基于M-Copula-SV-T模型的高维组合风险度量[J].中国管理科学，2017（2）：1～9.

[17] Rockafeller R. T.，Uryasev S. Optimization of Conditional Value-at-Risk[J].Risk，2000（3）：21～41.

[18]Rockafeller R. T.，Uryasev S. Conditional Valueat-Risk for General Loss Distributions[J].Journal of Banking and Finance，2002（7）：1443～1471.

[19] Artzner P.，Delbaen S.，Eber J. M.，et al. Thinking Coherently[J].Risk，1997（11）：68～71.

[20] Clark P. A Subordinated Stochastic Process Model with Finite Variance for Speculative Prices[J].Econometrica，1973（1）：135～155.

[21] Tauchen G.，Pitts M. The Price Variabilityvolume Relationship on Speculative Markets[J]. Econometrica，1983（2）：485～505.

[22] Hull J.，White A. Valuation of a CDO and an n-th to Default CDS Without Monte Carlo Simu？ lation[J].Journal of Derivatives，2004（2）：8～23.

[23]Taylor S. J. Modeling financial time series[M]. New York：John Wiley and Sons，1986：1～200.

[24] Liesenfeld R.，Jung R. Stochastic Volatility Models：Conditional Normality Versus Heavytailed Distributions[J].Journal of Applied Econo？ metrics，2000（2）：137～160.

[25]Koopman S.，Uspensky E. The Stochastic Volatility in Mean Model：Empirical Evidence from In？ ternational Stock Markets[J].Journal of Applied Econometrics，2002（6）：667～689.

[26] Taylor S. Modeling Stochastic Volatility：A Review and Comparative Study[J].Mathematical Finance，1994（2）：183～204.

[27] Geman S.，Geman D. Stochastic Relaxation，Gibbs Distributions，and the Bayesian Restoration of Images[J].IEEE Transactions on Pattern Analy？ sis and Machine Intelligence，1984（6）：721～741.

作者單位：1.中国人民大学商学院，北京100872；2.中国注册会计师协会，北京100039。宋烜为通讯作者