基于双拱作用的抗滑桩最大桩间距计算
2019-09-10李怀鑫范登政
李怀鑫 范登政



摘 要:为探讨边坡加固中抗滑桩最大桩间距问题,本文在已有研究基础上假定最大桩间距下双拱(端承拱和摩擦拱)同时存在,且双拱上的滑坡推力之和等于桩后滑坡推力,在此假设基础上,根据端承拱和摩擦拱的阻滑机理以及土体Mohr-Coulomb强度准则,采用解析法推导出了最大桩间距的计算公式,并在此基础上进一步分析了土体抗剪强度、抗滑桩截面尺寸等因素对桩间距的影响情况,并通过工程案例对最大桩间距的计算公式进行了验证.结果表明:最大桩间距随土体抗剪强度以及桩截面尺寸的增加而增加,且桩间距对桩正面宽度的敏感性要大于桩侧面宽度;端承拱承担的滑坡推力始终大于摩擦拱承担的滑坡推力.
关键词:抗滑桩;滑坡;桩间距;土拱效应;Mohr-Coulomb强度准则
中图分类号:TU753.3 文献标识码:A 文章编号:1673-260X(2019)12-0081-04
1 引言
抗滑桩的阻滑机理依靠于桩间土颗粒的楔紧效应,土颗粒楔紧效应越强,土拱效应越突出,抗滑桩阻滑效果越好,实际工程中,抗滑桩的加固机理即利用土拱效应,将滑坡推力传递到抗滑桩上,从而达到阻滑效果,因此分析土拱效应下最大桩间距对于滑坡治理具有重要意义.目前基于土拱效应下桩间距的计算方法主要为以下3种:?譹?訛利用抗滑桩桩侧摩阻力之和不小于桩间土拱上推力的条件以及拱顶或拱脚处的强度准则求解最大桩间距[1-4].?譺?訛基于桩土间的相互作用机制求解最大桩间距[5].?譻?訛基于统一强度理论求解最大桩间距[6].土体是一种各向异性材料,其固有的力学特性对土拱的形状及土拱的应力分布等均有影响,因此由桩间土拱受力特点进行分析有利于更好求解最大桩间距.相关研究成果表明[7],实际工程中,端承拱和摩擦拱同时存在且共同作用,虽然桩间土拱形式有所不同,但双拱联合作用下的极限承载力可近似为两单拱的极限承载力之和,此外,两单拱占据各自的主导区,本文在前人的研究成果上,基于Mohr-Coulomb强度准则及桩间土体静力平衡条件,综合考虑双拱的作用机理建立出最大桩间距的求解方法.
2 模型分析及计算
实际工程中抗滑桩截面大多为圆形和矩形,少数抗滑桩也存在梯形截面,本文以矩形截面抗滑桩进行计算,沿抗滑桩桩长方向,取单位厚度土拱进行受力分析,不计土拱、桩身自重以及土拱的三维现象,且假定拱后滑坡推力沿拱跨度方向均匀分布.由文献[7]可知,桩间土拱分为端承拱和摩擦拱,两者共同发挥阻滑作用,故假定端承拱承担的滑坡分力为p1,摩擦拱承担的滑坡分力为p2,土拱模型如图1,其中端承拱受力分析如图2.
3 桩间距计算
3.1 樁后土拱(端承拱)
单排矩形抗滑桩在桩间距设置合理的情况下,桩后拱脚处会形成三角形受压区[2-5](图3).
端承拱拱脚处为单向受力状态,沿着拱轴线方向的应力是大主应力,最不利剪切面与大主应力方向的夹角为45°-φ/2,故由图3及式(2)、(3)可得:
3.2 桩侧土拱(摩擦拱)
当两相邻桩侧摩阻力之和不小于作用于摩擦拱上的剩余滑坡推力时,桩后土拱效应才能正常发挥作用,由摩擦拱上的静力平衡条件可得:
由于摩擦拱与抗滑桩接触面为最不利破裂面(图4),对于矩形截面抗滑桩而言,最不利破裂面与最大主应力作用面夹角为(45°+φ/2)[4].
桩后滑坡推力沿桩深度方向具有不同的分布形式,应根据桩后滑坡推力的分布形式判断抗滑桩桩体最不利受力处位置,并在该深度下进行最大桩间距的计算.此外,由于降水会极大降低土体的抗剪强度从而导致滑坡现象发生,所以可由室内试验确定土体抗剪强度与含水率之间的函数关系来进一步求解最大桩间距,即:
4 算例分析
4.1 工程案例
本文工程实例来自文献[3],四川北部某高速公路堆积体路堑高边坡采用悬臂式抗滑桩支挡,桩后滑坡土体的平均重度γ=20kN/m3,快剪试验得土体黏聚力c=50kPa,内摩擦角φ=28°,抗滑桩采用C30混凝土浇筑,横截面矩形截面,其正面宽度b=2m,侧面宽度a=3m,桩全长22m,悬臂段长度11m.由于作用在抗滑桩上的荷载应当为拱后土体的剩余下滑力,因此采用传递系数法算得桩后的坡体推力偏于安全,故本文取桩后滑坡推力为E=1050kN/m,取单位厚度土拱受力分析可得拱后滑坡推力为q=95.45kpa,土体与抗滑桩之间的内摩擦角φ′取φ/2,此时由摩尔包线可知黏聚力c′=ctanφ′cotφ,将案例中相关参数代入式(10)中可计算出端承拱上的滑坡分力值p1=339kpa,相关参数代入式(16)可计算出摩擦拱上的滑坡分力值p2=269kpa,将滑坡分力值p1、p2代入式(1)计算可得l=6.37m.本文计算结果与其他计算结果见表1.
实际工程中采用的桩间距为6m,由此可见采用该方法确定最大桩间距是可行的,此外,通过表1可以看出不同方法计算的最大桩间距值有所不同,因此最大的桩间距的计算方法有待于更多的工程资料进行检验.
4.2 参数分析
通过对式(17)的分析可知影响桩间距的因素为土体强度指标c、φ,抗滑桩桩截面参数a、b,为进一步研究这些因素对桩间距的影响情况,仍以工程实例中的相关参数进行分析.
4.2.1 最大桩间距L与内摩擦角φ的关系
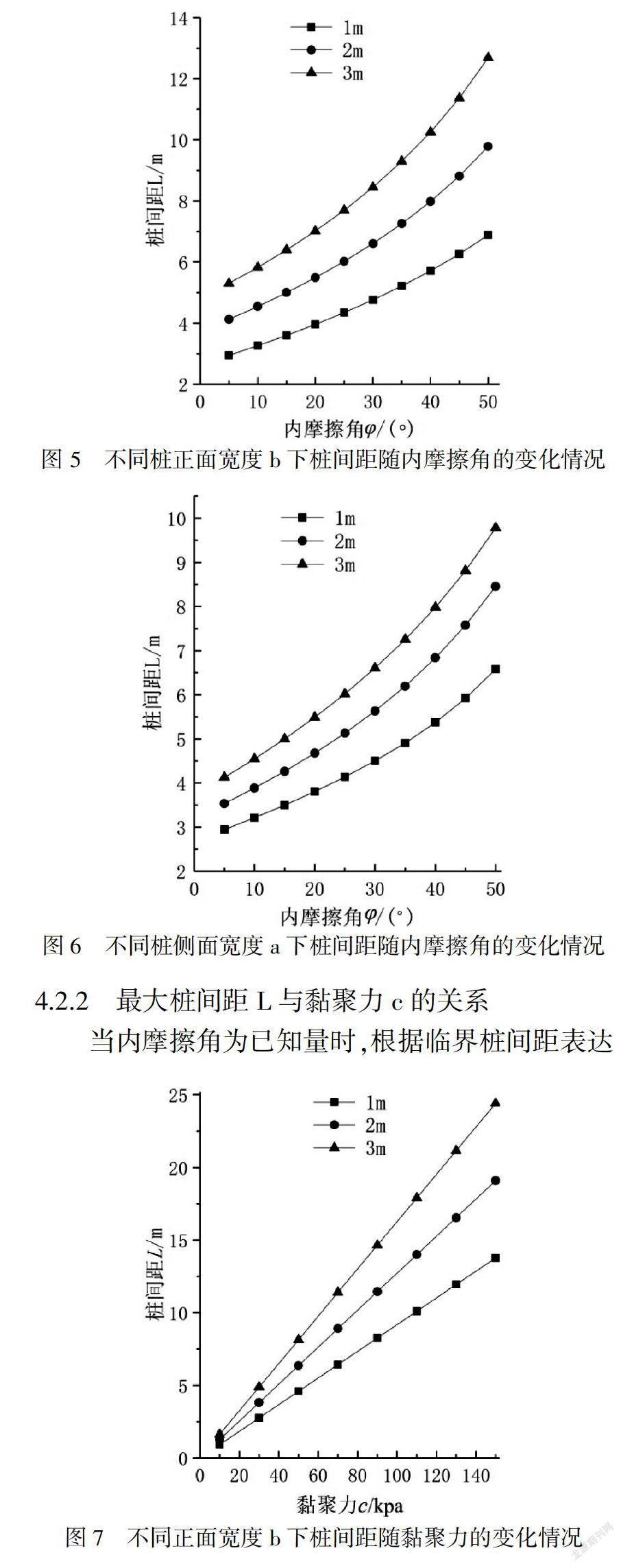
当黏聚力c为已知量时,根据临界桩间距表达式(17)可得抗滑桩侧面宽度为3m时,不同桩正面宽度b下最大桩间距L与内摩擦角φ的关系(图5)以及抗滑桩正面宽度为2m时,不同桩侧面宽度a下最大桩间距L与内摩擦角φ的关系(图6).
由图5~6可以看出不同桩截面尺寸下最大桩间距均随内摩擦角φ的增加呈曲线增加的形式,这是因为桩截面尺寸越大,抗滑桩与土体之间的接触面就越大,因此抗滑桩的阻滑效果越好,桩间距越大.此外,随着内摩擦角φ的增加,桩正面宽度b对桩间距的影响程度比桩侧宽度a对桩间距的影响程度要大.
4.2.2 最大桩间距L与黏聚力c的关系
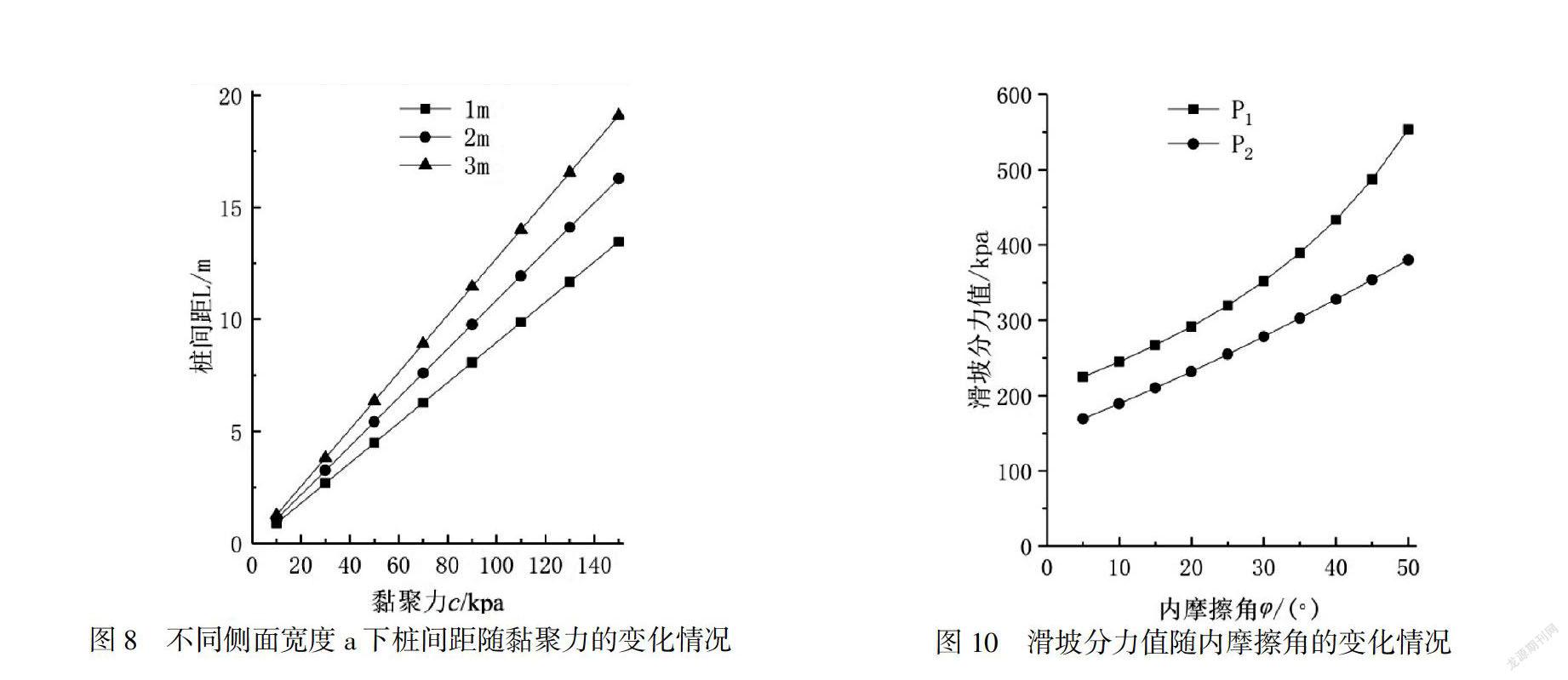
当内摩擦角为已知量时,根据临界桩间距表达式(17)可得抗滑桩侧面宽度为3m时,不同桩正面宽度b下最大桩间距L与黏聚力c的关系(图7)以及抗滑桩正面宽度为2m时,不同桩侧面宽度a下最大桩间距L与黏聚力c的关系(图8).
从图7~8可以看出不同桩截面尺寸下,最大桩间距随内摩擦角φ的增加均呈线性增加的形式,此外,随着黏聚力c的增加,桩正面宽度b对最大桩间距的影响程度比桩侧宽度a对最大桩间距的影响程度要大.
4.2.3 滑坡推力p与黏聚力c和内摩擦角φ的关系
由表达式(10)、(16)可得滑坡分力与黏聚力c和内摩擦角φ之间的关系(图9~10).由图9可以看出当内摩擦角φ为不变量时,双拱上滑坡分力值均随黏聚力c的增加而线性增加.由图10可以看出当黏聚力c为不变量时,端承拱上的滑坡分力随内摩擦角φ的增加呈曲线递增的关系,但摩擦拱上的滑坡分力随内摩擦角φ的增加呈线性增加的关系.此外,端承拱承担的滑坡分力P1值始终大于摩擦拱承担的滑坡分力P2值,且土体抗剪强度越大,两者的比值越大.
5 結论
a、滑坡土体的强度指标是影响最大桩间距的主要因素,抗滑桩截面尺寸是影响最大桩间距的次要因素,且最大桩间距对抗滑桩正面宽度的敏感性大于桩侧面宽度.
b、端承拱承担的滑坡推力始终大于摩擦拱承担的滑坡推力,且两者承担滑坡推力的比值随土体抗剪强度的增加而增加.
参考文献:
〔1〕周德培,肖世国,夏雄.边坡工程中抗滑桩合理桩间距德探讨[J].岩土工程学报,2004,26(1):132-135.
〔2〕赵明华,廖彬彬,刘思思.基于拱效应的边坡抗滑桩桩间距计算[J].岩土力学,2010,31(4):1211-1216.
〔3〕张玲,陈金海,赵明华.考虑土拱效应的悬臂式抗滑桩最大桩间距确定[J].岩土力学,2019,40(11):1-10.
〔4〕邱子义,韩同春,豆红强,等.桩后及桩侧土拱共同作用的抗滑桩桩间距分析[J].浙江大学学报(工学版),2016,50(3):559-565.
〔5〕肖世国,程富强.再论悬臂式抗滑桩合理桩间距的计算方法[J].岩土力学,2015,36(1):111-116.
〔6〕李长冬.抗滑桩与滑坡体相互作用机制及其优化研究[D].武汉:中国地质大学,2009.
〔7〕林治平,刘祚秋,商秋婷.抗滑桩结构土拱的分拆与联合研究[J].岩土力学,2012,33(10):3109-3114.
