高中数学建模的教学与探究

2019-09-10温茜茜

高考·下 2019年12期

温茜茜

摘要：本文对新高考模式下高中数学建模教学进行教学探究，文中以2008年美国中学生数学建模B题的抑制城市犯罪暴力问题为案例，在此建立回归分析数学模型对数据资料进行相关分析和预测.在构建解题的研究过程，针对高中学数学建模，介绍回归分析类型问题解决的建模方法和技巧，包括回归分析的类型、原理算法、编程计算、分析解决问题，培养和提高中学生数学建模能力。

关键词：新高考;高中数学;建模教学

一、回归分析模型

（一）问题的提出

犯罪暴力事件，失业人数，失业率，高中入学人数，高中辍学人数，毕业率，辍学率，入狱人口，假释人数，假释违反者，假释违反的百分比.对这些数据进行分析和建模，并为城市制定计划以减少犯罪暴力。

（二）回归分析基本类型及原理

变量之间的相互关系可分为确定性关系，也叫做函数关系，其特征是：一个变量随着其他变量的确定而确定;另一类关系叫相关关系，其特征是：变量之间的关系很难用一种精确的方法表示出来.由于存在测量误差等原因，或当对事物内部规律了解得更加深刻时，确定性关系和相关关系可能互相转化.

回归分析就是处理变量之间的相关关系的一种数学方法，是最常用的数理统计方法，能解决预测、控制、生产工艺优化等问题，有着广泛应用.回归分析一般分为线性回归分析与非线性回归分析.

线性回归又分一元线性回归和多元线性回归，其中一元线性回归为一个自变量，其模型是y=a+bx+ε，其中a为截距、b为回归直线的斜率，它们称回归系数，ε是随机误差.多元线性回归的自变量为多个，其模型是，其中b0是常数项，称为y对应于的偏回归系数，ε是随机误差.有时两个变量之间的关系可以不是线性的相关关系，而是某种曲线的相关关系，这种情况则需要构建曲线回归分析模型.

非线性回归即为曲线回归，又分为一元非线形和多元非线形.一元非线形回归（曲线回归）指的是一个自变量的非线形回归，主要有对数、反函数、抛物线、三次、复合、幂函数、指数、logistics等曲线方程.多元非线形回归指的是自变量有两个或两个以上的非线形回归.常见的六类曲线代换方法如下：

（1）双曲线;（2）幂函数曲线;（3）指数曲线，其中a>0;（4）倒指数曲线;（5）对数曲线，x>0;（6）S型曲线

（三）回归分析解题方法

回归分析的大概解题方法和步骤如下：

（1）数据整理（包含因变量和自变量）;

（2）选定因变量与自变量之间的模型（根据数据特征结合经验构建数学式子），利用数据按照最小二乘准则计算模型中的系数;

（3）利用统计分析方法对不同的模型进行比较，找出与数据拟合得最好得模型;

（4）判断得到的模型是否适合于这组数据;

（5）利用模型對因变量作出解释或预测.

（四）解题并得出结论

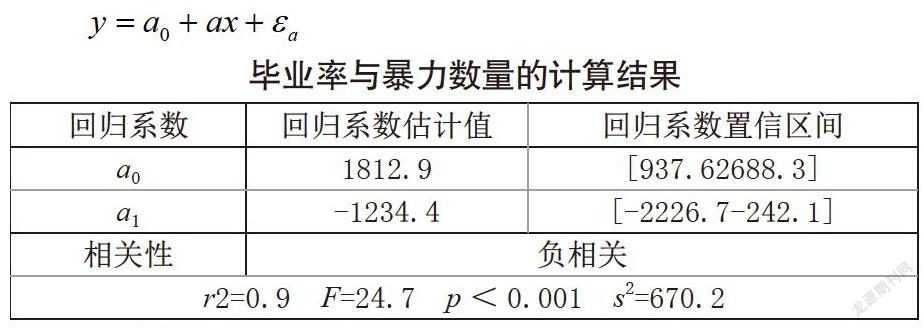
根据散点图及经验构建毕业率关于暴力数量的一元线性回归模型：

处理数据后，经过残差分析和检验，从相关性分析与回归分析的结果来看，毕业率与暴力事件相关，且呈现负相关.当毕业率越低，暴力事件越高;毕业率高，暴力事件数量降低.接着对其进行回归预测，可得出暴力事件数量下降，毕业率要呈增长趋势.