浅谈极值法在初中物理解题中的应用

马艳

摘要：习题训练乃是物理教学当中的重要部分，初中生通过习题解答这种仿古式，除了能够对所学知识进行深入理解以及灵活运用之外，同时还能把理论和实践进行结合，进而促使其知识运用这一能力得到发展以及提升。本文旨在探究初中时期物理解题教学当中极值法的具体运用，希望能给实际教学提供相应参考。

关键词：初中物理;解题;极值法

一、力学问题中极值法的运用

力学知识乃是初中物理当中的重要内容，其中包含很多不同内容，一直贯彻在整个知识学习当中，并且是初中生学习以及理解的一个重点以及难点。对力学问题加以解答之时，受力分析属于一个不可缺少的环节，通过受力分析可以得知物理实际状态，并且对其中含有的力学的关系式加以掌握，促使其对物理问题具体解答要点以及方法加以掌握。在这之中，极值法属于一种常见解题方法，通过拓展性解题思维加以分析，这样可以对解题步骤进行简化，避免大量计算，进而提升其解题效率，同时还能帮助学生对问题本质加以认识以及理解，提高其问题解决的质量。

比如，水面上漂浮着密度均匀的小木板，如今把水面之下虚线处的部分截去，问水中剩余部分的木块发生怎样的变化。

针对这个问题，在过去，初中生会按照题目信息，对截取先后小木块实施受力分析，这样可以得到物理重力和浮力相平衡，木块处在静止状态。而且，根据浮力表达式 ，把其和物体重力进行结合，并且列出关系式，之后通过对比物体截取先后的关系式，可以得到物体具体排水体积要有一定增量，从而完成问题解答。剩余木块会下降一段距离，之后满足重力和浮力相平衡。但是，在解答上述問题之时对极值法加以运用，可对条件加以适当扩大，将问题转变成把水面下木板截去，从而得到截去以后物体的排水量是0.这是，这个木板仅受重力作用，从而得到木板会进行下沉，进而得到缩减木板长度，则木板会发生下沉这一结果。而且，通过极值法可避免大量计算，提高初中生的解题效率以及正确率。

二、压强问题中极值法的运用

进行习题练习期间，压强是初中生重点学习的一个内容。在过去解题期间，一般在有关的物理关系实际分析以及对比当中，初中生经常出现一些错误，致使其解题能力难以提升。但在解答压强问题期间对极值法加以运用，可以让初中生形成清晰对比体系，从而拓展其解题思维，促使学生的解题效率以及正确率得以提高。

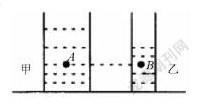
例如，如图所示在底面面积不同的两个圆柱形的容器之中，分别盛装不同液体，确保其对容器的底部具有相同大小的压强。在两个容器之后，分别在同一高度选择两个点，即A与B，试分析A与B两点的压强大小。

在过去解题步骤之中，初中生对通过压强相等这个已知条件把关系式列出来，即 ，通过甲容器当中液体高度比乙容器当中液面高度大，可以得到甲容器当中液体密度比乙容器当中液体密度小。之后，通过压强公式，可以分别把A与B两点处的压强列出来，从而结合现有条件进行分析，进而得到A点压强值大于B点压强值。

但通过极值法，可设A点与B点据底部距离是乙容器当中液体高度，从而得到B点在液面之上，所以压强是0.但A点位于液面之内，所以压强不是0，从而得到A点压强值大于B点压强值。这样一来，可以对解题步骤进行简化，不涉及到计算，可以提高初中生的解题效率以及准确率[1]。

三、电学问题中极值法的运用

一直以来，电学知识都是初中物理当中的重要部分，其拥有繁杂特诊，而且要求初中生对电学知识进行学习期间需要具备一定思维能力，注射羊才可对电学关系进行清楚认识，对电学问题进行正确解答。在对电学问题进行解答期间，可以对极值法加以运用，如在特定的条件之下，求电路电流以及电压最大值以及最小值;电路当中功率的最小值以及最大值等。初中生在对电学习题加以解答期间对极值法加以运用，可以对解题思路加以清晰掌握。第一，对电路图加以分析，根据电路特征，分析在何种情况之下能够出现极值现象，之后在极值条件之下，分析电路图具体结构、电压以及电流情况。此外，还需要初中生结合习题进行训练，进而对极值法在电学问题解答当中的具体应用方法加以掌握[2-3]。

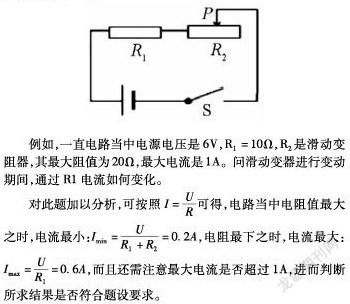
例如，一直电路当中电源电压是6V，R1=10Ω，R2是滑动变阻器，其最大阻值为20Ω，最大电流是1A。问滑动变器进行变动期间，通过R1电流如何变化。

对此题加以分析，可按照 可得，电路当中电阻值最大之时，电流最小： ，电阻最下之时，电流最大： ，而且还需注意最大电流是否超过1A，进而判断所求结果是否符合题设要求。

结论：综上可知，在初中时期物理教学之中，教师徐对解题方法以及解题技巧加以重视，帮助学生在解题当中对所学知识进行掌握，促使其把新旧知识进行融汇贯通。其中，极值法就是一种重要的解题方法，其在力学、压强以及电学问题当中有着重要应用。通过极值法可以降低问题难度，促使其解题能力得以提高。