一种SVPWM过调制算法在永磁牵引逆变器中的应用研究

张育超 徐鹏程

摘 要：为了提高地铁牵引逆变器直流母线电压利用率，扩展电动机运行范围，改善电动机的动态特性，有关部门应采用叠加原理的过调制处理算法，并应用在永磁同步电动机控制系统中，减小电压谐波畸变率，减小转矩波动。本文首先详细介绍该过调制算法原理，然后给出永磁同步电动机的运行方式及各个同步区的调制模式，最后在MATLAB/Simulink环境下，建立永磁同步电动机控制系统的仿真模型，并对基于叠加原理的过调制算法和传统单模式过调制算法进行对比仿真。

关键词：永磁同步电动机控制系统;过调制;牵引逆变器;叠加原理

中图分类号：TM341 文献标识码：A 文章编号：1003-5168（2019）14-0053-04

Application Research of SVPWM Overmodulation Algorithm

in Permanent Magnet Traction Inverter

ZHANG Yuchao1 XU Pengcheng2

（1.China Shipbuilding Industry Corporation No.713 Institute，Zhengzhou Henan 450000;

2.CSIC Haiwei Zhengzhou High-tech Co.， Ltd.，Zhengzhou Henan 450000）

Abstract： In order to increase the utilization ratio of DC bus voltage of subway traction inverter， extend the running range of motor and improve the dynamic characteristics of the motor， the relevant departments should adopt the overmodulation processing algorithm based on the superposition principle and apply it in the permanent magnet synchronous motor control system to reduce the voltage harmonic distortion rate and reduce the torque fluctuation. This paper first introduced the principle of the overmodulation algorithm in details， then gave the operation mode of the permanent magnet synchronous motor and the modulation mode of each synchronous zone. Finally， under the environment of MATLAB/Simulink， the simulation model of permanent magnet synchronous motor control system was established， and the over-modulation algorithm based on superposition principle was compared with the traditional single-mode over-modulation algorithm.

Keywords： permanent magnet synchronous motor control system;overmodulation;traction inverter;superposition principle

PWM技术是交流调速系统中的关键，常用的调制方法有SVPWM和SPWM两种。与SPWM方法相比，采用SVPWM方法，相电流波形的谐波成分低，电动机输出转矩波动较小，旋转磁场更逼近圆形，使直流母線电压利用率得到很大提高（SVPWM方法比SPWM方法的直流母线电压利用率提高15.47%），更易于实现数字化[1-4]。

永磁同步电动机在方波调制运行时，通过使用过调制控制方法，可以显著提高逆变器直流母线电压利用率[5-8]。现阶段，永磁同步电动机的调制控制方法主要有以下几方面。第一，把过调制区域根据调制度分为两段：过调制I段和过调制II段。把过调制I段和过调制II段进行线性分段，应用在异步电动机的V/F（变压变频）控制中，能够实现异步电动机从线性区到方波区的平滑过渡。第二，将一种新的基于叠加原理的SVPWM过调制算法应用在异步电动机的V/F控制中，采用该算法使电动机从线性区平顺过渡到方波区，且输出的基波电压幅值与调制度线性相关，输出中的谐波含量得到有效控制。第三，采用模型参考自适应方法辨识电动机转子方位，并采用单模式过调制算法控制逆变器，使电动机在无传感器的情况下也能实现过调制矢量控制。第四，对一种采用简单算法SVPWM过调制算法的各阶段磁链特性进行分析，将该过调制算法应用在永磁同步电动机控制系统中，对电动机的运行特性进行仿真研究，结果表明：过调制算法加快了电动机的响应进程，扩展了电动机运行速度的范围。

本文以第一种算法为基础，先从理论公式推导入手，得出一种更简便的基于叠加原理的SVPWM过调制算法，并应用在永磁同步电动机上。该算法不仅易于数字实现，而且能够减少永磁同步电动机的输出相电压谐波含量。为了验证其有效性，在MATLAB/Simulink环境下建立永磁同步电动机控制系统的仿真模型，对基于叠加原理的过调制算法和传统单模式过调制算法进行对比仿真，结果表明：采用基于叠加原理的过调制算法，输出相电压谐波含量得到明显抑制，转矩波动较小。

1 SVPWM过调制概念

1.1 基本原理

定义调制度m为：

[m=3VrefVdc]                                （1）

式中：[Vref]为目标参考电压矢量的幅值;[Vdc]为直流母线侧电压值。线性调制段不在本文讨论范围内，本文主要研究过调制I段与过调制II段。过调制I段与过调制II段的临界条件是参考电压矢量沿正六边形的轨迹运行，根据伏秒平衡原理，此时对应的参考电压矢量为：

[Vref=6×0.5×23Vdc×Vdc3π]                 （2）

进而可以推出在此临界点上的[m]为1.050 1。

1.2 过调制I段

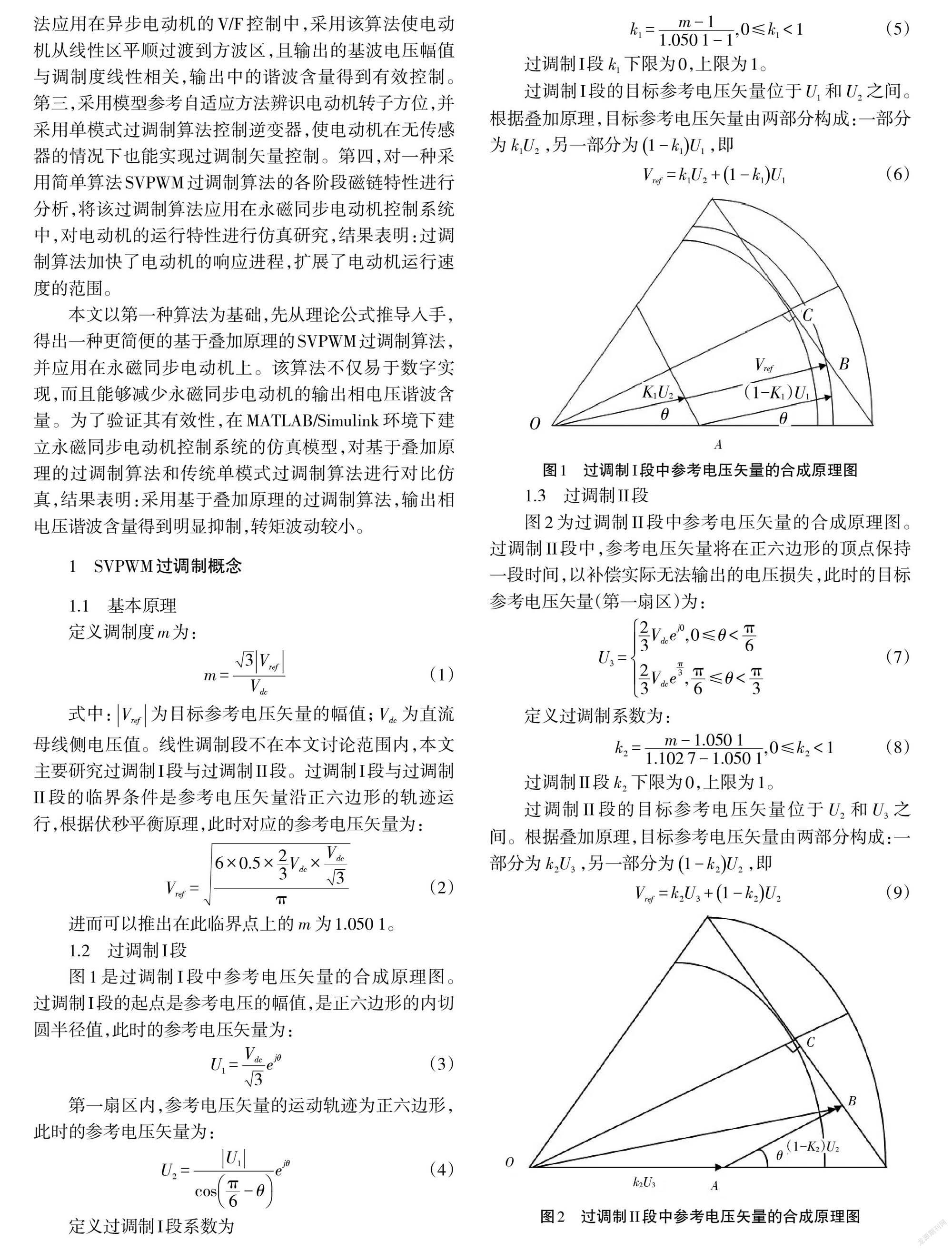
图1是过调制I段中参考电压矢量的合成原理图。过调制I段的起点是参考电压的幅值，是正六边形的内切圆半径值，此时的参考电压矢量为：

[U1=Vdc3ejθ]                                 （3）

第一扇区内，参考电压矢量的运动轨迹为正六边形，此时的参考电压矢量为：

[U2=U1cosπ6-θejθ]                               （4）

定义过调制I段系数为

[k1=m-11.050 1-1，0≤k1<1]                  （5）

过调制I段[k1]下限为0，上限为1。

过调制I段的目标参考电压矢量位于[U1]和[U2]之间。根据叠加原理，目标参考电压矢量由两部分构成：一部分为[k1U2]，另一部分为[1-k1U1]，即

[Vref=k1U2+1-k1U1]                      （6）

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼0（C$U{2V@DKI]HYH（CEY）0T.png>[A][O][θ][θ][K1U2][（1-K1）U1][Vref][B][C]

图1 过调制I段中参考电压矢量的合成原理图

1.3 过调制II段

图2为过调制II段中参考电压矢量的合成原理图。过调制II段中，参考电压矢量将在正六边形的顶点保持一段时间，以补偿实际无法输出的电压损失，此時的目标参考电压矢量（第一扇区）为：

[U3=23Vdcej0，0≤θ<π623Vdceπ3，π6≤θ<π3]                           （7）

定义过调制系数为：

[k2=m-1.050 11.102 7-1.050 1，0≤k2<1]           （8）

过调制II段[k2]下限为0，上限为1。

过调制II段的目标参考电压矢量位于[U2]和[U3]之间。根据叠加原理，目标参考电压矢量由两部分构成：一部分为[k2U3]，另一部分为[1-k2U2]，即

[Vref=k2U3+1-k2U2]                       （9）

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼`HUM98@CT]I）JRSLCVZ8KR2.png>[A][k2U3][θ][（1-K2）U2][C][B][O]

图2 过调制II段中参考电压矢量的合成原理图

2 电动机运行方式

地铁牵引传动系统逆变器的最高开关频率通常比较低，而牵引电动机的最高输出频率可以达到266Hz，导致载波比有很大的浮动空间。为充分利用逆变器的最高开关频率，本文采用多模式调制策略，即根据速度的不同灵活采用异步调制、分段同步调制、方波调制相结合的方式。异步调制在低速区使用，分段同步调制在中速区使用。

中速区根据调制度分别进入同步15、11、7、3脉冲调制。其中，同步15脉冲调制采用传统空间矢量策略（Conventional Space Vector Strategy，CSVS），采用调制度切换;同步11、7、3脉冲调制采用基本母线钳位策略（Basic bus clamping strategy，BBCS）。各种调制模式对应的频率范围和调制度（括号内为调制度）范围如图3所示。

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼13EP@@BIQDH[V9PA@F）N）[7.png>[fc/Hz][1 320][异步][15P][11P][7P][3P][1P][fs/Hz][133][110][87][66][（0.53）][（0.75）][（0.9）][（0.98）]

图3 牵引工况下的脉冲模式

3 仿真实验研究

3.1 仿真平台

永磁同步电动机控制系统的仿真模型主要分为三部分，即转矩给定模块、主电路仿真模块及控制和调制算法模块，如图4所示。转矩给定模块负责把转矩指令给到控制系统中;主电路仿真模块主要由永磁同步电动机模型和三相两电平逆变器模型构成，实现机械和能量转换仿真;控制与调制算法仿真模块，主要由自定义M函数模型和基本运算模型构成，通过对主电路永磁电动机的三相电流和速度信号、逆变器母线电压和输出电流进行实时采样，经过自定义函数模型运算后输出PWM脉冲，控制逆变器完成永磁电动机牵引、制动转矩特性。

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼image27.png>

图4 永磁同步电动机控制系统的仿真模型

电动机仿真参数如表1所示。

3.2 仿真结果

永磁同步电动机采用异步调制起动，然后过渡到同步调制区。调制度分别为0.53、0.75、0.9、0.98时，调制方式切换为同步15脉冲、同步11脉冲、同步7脉冲和同步3脉冲。在调制度大于1时，通过过调制算法从同步3脉冲调制平滑过渡到方波调制。为防止相邻调制模式之间来回切换，引发过流故障，在程序中设置调制度为0.02的滞环。对于过调制算法，主要采用传统单模式过调制算法和基于叠加原理的过调制算法，并进行对比仿真。

表1 永磁同步电动机仿真参数

[电动机参数 参数值 定子电阻/mΩ 33 直轴电感/mH 2.67 交轴电感/mH 3.91 极对数 4 永磁体磁链/Wb 0.869 4 额定电压/V 1 000 额定电流/A 116.4 额定频率/Hz 133.3 额定功率/kW 180 直流母线电压/V 1 500 ]

根据不同区间调制度m取值不同，过调制I区内为1.02，过调制II区内为1.08，此时输出的线电压频谱图如图5、6所示。由图可知，调制度为1.02时，传统单模式过调制算法下的输出线电压总谐波畸变率为30.99%，基于叠加原理的过调制算法下的输出线电压总谐波畸变率为24.02%;调制度为1.08时，传统单模式过调制算法下的输出线电压总谐波畸变率为34.69%，基于叠加原理的过调制算法下的输出线电压总谐波畸变率为30.34%。与传统单模式过调制算法相比，采用基于叠加原理的过调制算法，逆变器输出线电压总谐波畸变率（Total Harmonic Distortion，THD）较低。

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼image29.png>[THD=30.99%][f/Hz][幅值/%][100

80

60

40

20

0

][0         &nbsp;    200            400            600          800         1 000]

（a） 輸出线电压频谱图（单模式过调制算法）

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼image30.png>[THD=24.02%][幅值/%][100

80

60

40

20

0

][0              200             400            600            800         1 000][f/Hz]

（b） 输出线电压频谱图（基于叠加原理的过调制算法）

图5 m=1.02时两者输出线电压频谱图

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼image32.png>[幅值/%][100

80

60

40

20

0

][0              200             400            600            800         1 000][THD=34.69%][f/Hz]

（a） 输出线电压频谱图（单模式过调制算法）

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼image33.png>[幅值/%][100

80

60

40

20

0

][0    100    200   300   400    500   600    700    800    900   1 000][f/Hz][THD=30.34%]

（b） 输出线电压频谱图（基于叠加原理的过调制算法）

图6 m=1.08时两者输出线电压频谱图

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼image35.png>[Te/N·m][][1 500

1 000

500

0][16   16.2  16.4  16.6  16.8     17   17.2  17.4  17.6 17.8    18][t/s]

（a） 输出转矩曲线（单模式过调制算法）

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼image36.png>[Te/N·m][][1 000

500

0][16   16.2   16.4  16.6  16.8    17   17.2   17.4  17.6  17.8    18][t/s]

（b） 输出转矩曲线（基于叠加原理的过调制算法）

图7 过调制区的输出转矩曲线

图7是两种算法下的输出转矩波形。在过调制区，基于叠加原理的过调制算法下的转矩波动为80N·M左右，小于传统单模式过调制算法下的转矩波动（150N·M左右）。

4 结语

本文在详细介绍基于叠加原理的SVPWM过调制算法和牵引永磁同步电动机运行方式的基础上，在MATLAB/Simulink环境下，建立永磁同步电动机控制系统的仿真模型，对传统单模式过调制算法和基于叠加原理的过调制算法进行对比仿真。结果表明：采用基于叠加原理的过调制算法，输出相电压谐波含量得到明显抑制，转矩波动较小。

参考文献：

[1]梁伟华，郗晓田，游林儒，等.一种扩展SVPWM线性调制区及过调制算法实现[J].电力电子技术，2013（5）：10-12.

[2]韦克康.轨道牵引逆变器数字控制研究[D].北京：北京交通大学，2012.

[3] Grahame Homes D， Lipo Thomas A.Pulse Width Modulation for Power Converters：Principles and Practice[D].New York：IEEE Press & Wiley Publishing，2003.

[4] Holtz J. Pulsewidth Modulation for Electronic Power Conversion[J].Proceedings of the IEEE，1994（8）：1194-1214.

[5] Holtz J.Pulsewidth Modulation-a Survey[J].IEEE Trans on Industrial Electronics，1992（5）：410-420.

[6]陆海峰，瞿文龙，张磊，等.基于调制函数的SVPWM算法[J].電工技术学报，2008（2）：37-43.

[7]张立伟，刘钧，温旭辉，等.基于基波电压幅值线性输出控制的SVPWM过调制新算法[J].中国电动机工程学报，2005（19）：12-18.

[8]杨澜倩，唐校，万频，等.SVPWM过调制算法磁链分析及在永磁同步电动机驱动中的应用[J].电动机与控制应用，2014（7）：6-9.