基于FRFT算法的移动平台水声信道编解码技术研究

柴林峰 刘倩倩

摘 要：本文提出基于LFM-FRFT（线性调频-分数阶傅里叶变换）的联合信道编解码方式，在接收机端通过检测LFM上下扫频来解码通信体制。LFM信号具有不敏感性，而FRFT通过分数阶域能够有效检测LFM信号，达到解决多普勒引起的接收机信道不匹配问题。

关键词：水声通信;分数阶傅里叶变换;LFM

中图分类号：TN929.3 文献标识码：A 文章编号：1003-5168（2019）14-0008-04

Underwater Acoustic Channel of Mobile Platform

Based on FRFT Algorithm Research on Coding and Decoding Technology

CHAI Linfeng1，2 LIU Qianqian1，2

（1.The 27th Research Institute of China Electronic Technology Group Corporation，Zhengzhou Henan 450047;2.Zhengzhou Key Laboratory of Underwater Information System Technology，Zhengzhou Henan 450000）

Absratct： This paper proposed a joint channel coding and decoding method based on LFM-FRFT （Linear Frequency Modulation-Fractional Fourier Transform）， which decoded the communication system by detecting LFM up-and-down sweep at at the receiver. Because of the Doppler insensitivity of LFM signal， FRFT can detect LFM signal effectively in fractional order domain to solve the channel mismatch problem caused by Doppler.

Keywords： underwater acoustic communication;;Fractional Fourier Transform;LFM

多普勒频移对水声通信系统产生了很大影响。长久以来，水声通信领域工作者在对抗多普勒方面做出了很大努力，传统的通信编码较多采用PSK、FSK、OFDM、DSSS等方式。但是，在水声信道中应用这些信道编码方式存在较多问题，例如，PSK和FSK如果需要更远的通信距离，则需要更大的瞬时功率，况且这两种通信方式抗噪声性能不佳;OFDM和DSSS虽然将信道能量拓展到一个带宽内，降低了通信系统的瞬时功率，但是OFDM先天对多普勒具有敏感性，导致多普勒破坏子载波的正交性，引起接收机解码困难;DSSS虽然通过接收机长时间累积，具有很强的抗干扰能力，但是对多普勒所引起的信号不相干问题，会导致累积增益优势不明显。因此，设计一种适合于水声信道的高可靠性和多环境适应性的信道编码方式显得尤为急迫，一方面要参考无线电的编码方式，但不能照搬;另一方面，要充分结合水声信道的特点。本文运用Kebkal提出的扫频-扩频调制方式[1，2]，结合扫频信号的特点，改进接收机系统，采用LFM-FRFT的联合信道编解码方式快速完成信道解码，适合工程化应用。

1 LFM信道编码原理

线性调频信号的构造方程为：

[yLFMt=A·expj2πf0t+πKt2+snK=BT-T2tT2]         （1）

其中，[A]為信号增益;[f0]为线性调频信号的中心频率;[K]为调制斜率;[B]为调制带宽;[T]为调制周期;[sn]为噪声;fd为多普勒。

当[K>0]时，输出的线性调频信号称为上扫频，记为：[yLFM+t];当[K<0]时，输出的线性调频信号称为下扫频，记为[yLFM-t]。

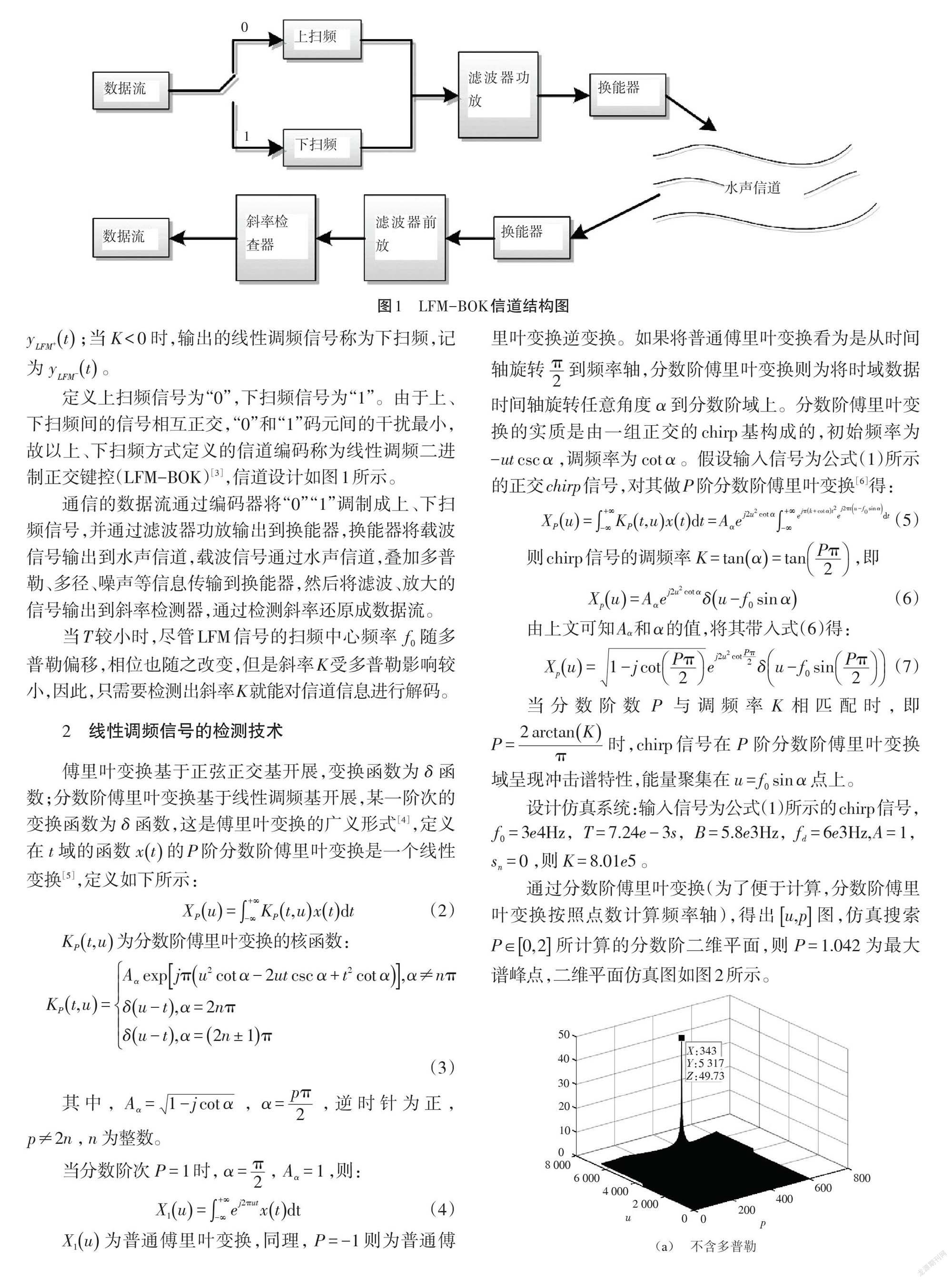
定义上扫频信号为“0”，下扫频信号为“1”。由于上、下扫频间的信号相互正交，“0”和“1”码元间的干扰最小，故以上、下扫频方式定义的信道编码称为线性调频二进制正交键控（LFM-BOK）[3]，信道设计如图1所示。

通信的数据流通过编码器将“0”“1”调制成上、下扫频信号，并通过滤波器功放输出到换能器，换能器将载波信号输出到水声信道，载波信号通过水声信道，叠加多普勒、多径、噪声等信息传输到换能器，然后将滤波、放大的信号输出到斜率检测器，通过检测斜率还原成数据流。

当T较小时，尽管LFM信号的扫频中心频率[f0]随多普勒偏移，相位也随之改变，但是斜率K受多普勒影响较小，因此，只需要检测出斜率K就能对信道信息进行解码。

2 线性调频信号的检测技术

傅里叶变换基于正弦正交基开展，变换函数为[δ]函数;分数阶傅里叶变换基于线性调频基开展，某一阶次的变换函数为[δ]函数，这是傅里叶变换的广义形式[4]，定义在[t]域的函数[xt]的P阶分数阶傅里叶变换是一个线性变换[5]，定义如下所示：

[XPu=-∞+∞KPt，uxtdt]                （2）

[KPt，u]为分数阶傅里叶变换的核函数：

[KPt，u=Aαexpjπu2cotα-2utcscα+t2cotα，α≠nπδu-t，α=2nπδu-t，α=2n±1π]（3）

其中，[Aα=1-jcotα]，[α=pπ2]，逆时针为正，[p≠2n]，[n]为整数。

当分数阶次[P=1]时，[α=π2]，[Aα=1]，则：

[X1u=-∞+∞ej2πutxtdt]                            （4）

[X1u]为普通傅里叶变换，同理，[P=-1]则为普通傅里叶变换逆变换。如果将普通傅里叶变换看为是从时间轴旋转[π2]到频率轴，分数阶傅里叶变换则为将时域数据时间轴旋转任意角度[α]到分数阶域上。分数阶傅里叶变换的实质是由一组正交的chirp基构成的，初始频率为[-utcscα]，调频率为[cotα]。假设输入信号为公式（1）所示的正交chirp信号，对其做P阶分数阶傅里叶变换[6]得：

[XPu=-∞+∞KPt，uxtdt=Aαej2u2cotα-∞+∞ejπk+cotαt2ej2πtu-f0sinαdt]（5）

则chirp信号的调频率[K=tanα=tanPπ2]，即

[Xpu=Aαej2u2cotαδu-f0sinα]                     （6）

由上文可知Aα和α的值，将其带入式（6）得：

[Xpu=1-jcotPπ2ej2u2cotPπ2δu-f0sinPπ2] （7）

当分数阶数[P]与调频率K相匹配时，即[P=2arctanKπ]时，chirp信号在[P]阶分数阶傅里叶变换域呈现冲击谱特性，能量聚集在[u=f0sinα]点上。

设计仿真系统：输入信号为公式（1）所示的chirp信号，[f0=3e4Hz，T=7.24e-3s，B=5.8e3Hz，fd=6e3Hz，A=1，][sn=0]，则[K=8.01e5]。

通过分数阶傅里叶变换（为了便于计算，分数阶傅里叶变换按照点数计算频率轴），得出[u，p]图，仿真搜索[P∈0，2]所计算的分数阶二维平面，则[P=1.042]为最大谱峰点，二维平面仿真图如图2所示。

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼image47.png>[50][40][30][20][10][0][8 000][6 000][u][4 000][2 000][0][0][200][400][600][800][X：343][p][Y：5 317][Z：49.73]

（a） 不含多普勒

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第14期_103928＼Image＼image48.png>[50][40][30][20][10][0][8 000][6 000][4 000][2 000][u][0][0][200][400][600][800][p][X：343][Y：5 751][Z：48.09]

（b） 含多普勒

图2 [u，p]平面二维图

P=0.7∶0.001∶1.3，P轴为0～600，步长为0.001的量化，则P=1.042时分数阶傅里叶变换为能量聚集的冲击特性。增加多普勒后的分数阶变换只是在u轴位置有偏移，依然能够检测出脉冲特性。由此可见，分数阶傅里叶变换对于大多普勒的线性调频检测能力要比匹配滤波方式更有优势。

3 湖泊实验

由于仿真环境无法完全仿真实际环境，无法仿真真实信道所引起相位、幅度等影响因素，因此，基于理论仿真研究进行实际环境验证具有重要意义。

实验地点：丹江口水库。实验环境：两台模拟通信机相距750m互相对法信号。实验水深：20m。水文环境：良好水况。在一台模拟通信机旁布设B&;K水听器，实验全程采集通信数据，设置采集器采样率[fs]=131 072Hz，则所对应的频率轴采样点数和时间的关系为：[n=T×fs]，对应采样点数和频率轴的关系为：[f=fsNn]，即[Kn=Kfs]，分数阶傅里叶变换为了计算方便按照点数输入计算。设计实验参数如表1所示。

表1 实验参数

[实验序号 起始频率[f1]/Hz 持续时间T/s 调制带宽B/Hz 调制斜率：

K（Hz/s） 调制斜率

Kn（n_f/n_t） 多普勒

fd/Hz 1 20e3 3.9e-3 -3.6e3 -9.23e5 -7.026 4 0 2 20e3 3.9e-3 -3.6e3 -9.23e5 -7.026 4 2e2 ]

通过设计以上表格，测试在多种不同参数下的系统检测性能。图3为采集时域波形图;图4为时域-频域波形图;图5为分数阶傅里叶变换结果。

由图5（b）可以看出，通过增加多普勒，信号时间长度会压缩，但是在分数阶域所对应的P值大致不变，为P值对应的310量化點，即P（310）=1.090，即分数阶系数P=1.090时出现能量聚集，[Kn=tanp×π2=-7.026 4]，[K=Kn×fs=-9.3e5Hz/s]，与设计条件一致。

（a） 时域信号

（b） 一帧数据放大图

（a） 时域波形

（b） 频谱图

（a） 实验1分数阶域图

4 结论

通过以上实验数据可以发现，分数阶傅里叶变换对于基于chirp的调制波形检测具备优势，相对于传统匹配滤波的方式，不受多普勒影响，且能有效估计多普勒频移，通过对分数阶系数P的估计，能够计算出调制斜率。分数阶傅里叶变换的特性是针对不同系数的能力叠加，针对不同P值具备能量累积效应。通过设计相应的解调通信机能够提高检测灵敏度，比传统的调制与解调方式具备优势。chirp信号由于其在频域展宽，瞬时能量低，具备抗干扰能力强、通信隐匿性强等优势，因此，基于chirp信号的分数阶傅里叶变换成为一种更具有优势的通信调制与解调方式。但是，由于分数阶系数P估计需要搜索，每次步长搜索需要做一次分数阶傅里叶变换，对于P值的估计计算量过大。

参考文献：

[1] Kebkal K G， Bannasch R. Sweep-spread Carrier for Underwater Communication over Acoustic Channels with Strong Multipath Propagation[J]. The Journal of the Acoustical Society of America，2002（5）：2043.

[2] Kebkal Konstantin G， Rudolf Bannasch. Implementation of a Sweep-spread Function for Communication over Underwater Acoustic Channels[C]// OCEANS 2000 MTS/IEEE Conference and Exhibition，2000（3）：1829-1837.

[3]王开兴.基于Chirp扩频的移动平台水声通信技术研究[D].杭州：浙江大学，2015.

[4]齐林，陶然，周思永，等.基于分数阶傅里叶变换的线性调频信号的自适应时频滤波[J].兵工学报，2003（4）：499-503.

[5] Almeida. The Fractional Fourier Transform and Time-frequency Representations[J]. IEEE Transactions on Signal Processing，1994（11）：3091.

[6]王文俊.基于FRFT的Chirp水声扩频通信技术研究[D].厦门：厦门大学，2014.