基于Matlab图形用户界面的期权定价系统开发及应用

2019-09-10张铮铎杨德平

青岛大学学报（工程技术版） 2019年2期

张铮铎杨德平

摘要：针对期权定价模型在金融衍生品定价过程中存在的问题，本文开发了基于Matlab GUI的期权定价系统，实现证券和利率衍生品价格及敏感性的计算。该系统以BlackScholes、CRR模型、HW模型等期权定价模型为基础，通过GUI空间的布局设计及回调函数的程序编写，选取欧式期权和亚式期权的数据，运用期权定价模型分别计算价格和敏感度，验证了将期权定价通过GUI实现的可行性，并以某笔期限为4年的贷款为例进行帽子期权的计算验证。验证结果表明，该系统界面友好，操作简单，准确实现了各类金融衍生品的定价。该研究使用户更加方便快捷的实现期权定价，提高了工作效率。

关键词： Matlab GUI; 金融衍生品; 期权定价模型; 敏感度

中图分类号： F830.91; TP317.4 文献标识码： A

随着金融市场的蓬勃发展，国内企业、银行等金融机构和非金融机构的投资者越来越多地使用金融衍生品进行交易和规避风险。在金融衍生品的应用过程中，如何合理有效的定价成为关键问题，因此各国学者对期权定价模型进行研究，并取得突破性发展[12]。然而期权定价模型对于普通投资者太过复杂，因此开发一款界面友好、操作简单的期权定价系统成为研究重点。近年来，图形用户界面（graphical user interface，GUI）引起了许多学者的关注，刘芳等人[3]运用GUI构建了电力电子电路仿真平台;孙祥等人[4]运用GUI设计开发系统，对信号及图像处理进行研究。还有一些学者将Matlab GUI设计开发系统应用于经济领域，年兴等人[5]研究了基于SVW的股指预测模型与GUI仿真;杨晓等人[6]运用Matlab GUI开发出马氏链股价预测系统，并给出在实际股价预测过程中的应用。在对各种期权定价及敏感度研究方面也有较快的进展;叶志强等人[7]拓展出满足实际需要的利率期权的隐含波动率表达式;李秉祥[8]研究了在有效期股票有连续分红的情况下，对欧式期权定价的BS模型进行了推广;刘春艳等人[9]利用Matlab绘制了看涨期权的敏感性指标曲线，并研究其变化规律;安占强等人[10]将标准二叉树定价模型延伸至非正态期权定价模型;张铁[11]利用随机误差校正方法，构造出可计算各种期权价格的新型二叉树参数模型;郭子君等人[12]证明了三叉树公式定价是BlackScholes公式定价的近似;郑小迎等人[13]创建了能够反映亚式期权路径依赖特征的多因素定价模型;王维国等人[14]结合几何亚式期权敏感性参数的估计，推导出算数亚式期权价格敏感性参数估计方法。基于此，本文以各类期权定价模型为理论基础，运用GUI开发期权定价系统，并选取实例对各类期权进行期权价格和敏感度计算。该研究对投资者应用期权有很好的指导意义。

2 期权定价系统的GUI开发

2.1 期权定价主系统

2.1.1 界面组成与布局

该期权定价系统每个界面的开发需经过各个系统的页面布局[1920]、空间属性设计、程序设计和产生具有功能的GUI等系统开发过程，每个界面都是独立的子系统。期权定价系统编辑器窗口如图1所示。该窗口是期权定价系统的主界面，主要设计了3个按钮来引导欧式期权定价、亚式期权定价、帽子期权定价3个子系统。

2.1.2 程序设计

4个按钮的回调函数如下：

1） “欧式期权定价”按钮的回调函数：

functionoushidingjia_Callback（hObject，eventdata，handles）

oushiqiquan

2） “二叉树模型对亚式期权定价”按钮的回调函数：

functionyashidingjia_Callback（hObject，eventdata，handles）

yashiqiquan

3） “HW模型对帽子期权定价”按钮的回调函数：

functionmaozidingjia_Callback（hObject，eventdata，handles）

maoziqiquan

4） “关闭系统”按钮的回调函数：

function guanbi_Callback（hObject，eventdata，handles）

close qiquandingjiaxitong

2.2 欧式期权定价子界面

2.2.1 界面组成与布局

本界面通过BS模型和Black模型对欧式期权进行定价和隐含波动率的计算[14]，界面内容主要包括输入数据、计算期权价格、计算隐含波动率及计算期权价格变动的敏感程度[15]（包括Delta、Lambda、Rho、Theta、Gamma、Vega的计算）。

2.2.2 主要代码

主要回调函数代码如下：

[Call1，Put1] =blsprice（Price，Strike，Rate，Time，Volatility）;%BS模型計算期权价格

[Call2，Put2] = blkprice（Price，Strike，Rate，Time，Volatility）;%Black模型计算期权价格

%计算期权隐含波动率

Volatility1c = blsimpv（Price，Strike，Rate，Time，Value1c）;

Volatility1p = blsimpv（Price，Strike，Rate，Time，Value1p）;

Volatility2c = blkimpv（Price，Strike，Rate，Time，Value2c）;

Volatility2p = blsimpv（Price，Strike，Rate，Time，Value2p）;

%计算期权价格变动的敏感度

[CallDelta，PutDelta] = blsdelta（Price，Strike，Rate，Time，Volatility，Yield）;

Gamma =blsgamma（Price，Strike，Rate，Time，Volatility，Yield）;

[Calllambda，Putlambda]=blslambda（Price，Strike，Rate，Time，Volatility，Yield）;

[CallRho，PutRho] = blsrho（Price，Strike，Rate，Time，Volatility，Yield）;

[CallTheta，PutTheta] =blstheta（Price，Strike，Rate，Time，Volatility，Yield）;

Vega = blsvega（Price，Strike，Rate，Time，Volatility，Yield）;

2.3 亚式期权定价子界面

2.3.1 界面组成与布局

本界面通过二叉树模型（coxrossrubinstein model，CRR）、等概率模型（equal probability model，EQP）[1617]和标准三叉树模型对亚式期权[18]定价，界面内容主要包括输入证券特征、输入利率结构、输入时间格式、输入亚式期权数据以及树结构的构建和期权价格的计算[1920]。

2.3.2 主要代码

主要回调函数代码如下：

%输入标的资产格式

StockSpec=stockspec（Sigma，AssetPrice，DividendType，DividendAmounts，ExDividendDates）;

RateSpec=intenvset（′Compounding′，Compounding，′Rates′，Rates，′StartDates′，StartDates，′EndDates′，EndDates）;%输入无风险利率格式

TimeSpec = crrtimespec（ValuationDate;Maturity;NumPeriods）;%CRR模型的时间离散格式

CRRTree=crrtree（StockSpec，RateSpec，TimeSpec）;%建立CRR型二叉树

Treeviewer（CRRTree） %显示CRR型二叉树结构

%CRR模型计算亚式期权价格

Price=asianbycrr（CRRTree，OptSpec，Strike，Settle，ExerciseDates，AmericanOpt）;

TimeSpec = eqptimespec（ValuationDate，Maturity，NumPeriods）;%EQP模型的时间离散格式

EQPTree=eqptree（StockSpec，RateSpec，TimeSpec）;%建立EQP型二叉树

treeviewer（EQPTree） %显示CRR型二叉树结构

%EQP模型计算亚式期权价格

Price=asianbyeqp（EQPTree，OptSpec，Strike，Settle，ExerciseDates，AmericanOpt）;

TimeSpec = stttimespec（ValuationDate，Maturity，NumPeriods）; %STT模型的时间离散格式

STTTree=stttree（StockSpec，RateSpec，TimeSpec）; %建立标准三叉树

Treeviewer（STTTree） %显示标准三叉树结构

%STT模型计算亚式期权价格

Price=asianbystt（STTTree，OptSpec，Strike，Settle，ExerciseDates，AmericanOpt）;

2.4 帽子期权定价子界面

2.4.1 界面组成与布局

本界面通过HW模型对利率衍生品中的帽子期权定价，界面内容主要包括输入利率波动特征、输入利率结构和输入时间格式来构建树结构，再输入帽子期权数据进行价格的计算[13]。

2.4.2 主要代码

主要的回调函数代码如下：

%输入HW模型利率波动率格式

VolSpec = hwvolspec（ValuationDate，VolDates，VolCurve，AlphaDates，AlphaCurve）;RateSpec=intenvset（′Rates′，Rates，′StartDates′，StartDates，′EndDates′，EndDates）;

%輸入HW模型树图的时间格式

TimeSpec = hwtimespec（ValuationDate，Maturity，Compounding）;

HWTree = hwtree（VolSpec，RateSpec，TimeSpec）;%建立HW模型利率树

Treeviewer（HWTree）%显示HW型树图结构

[Delta，Gamma，Vega，Price] = hwsens（HWTree，InstSet）;%计算期权价格和敏感度

3 期权定价系统应用实例

3.1 欧式期权定价

假设期权標的资产股票价格为50元，波动率标准差为0.5，无风险利率为10%，期权执行价为95元，存续期为0.25年，存续期股票无红利，计算该股票欧式期权价格、隐含波动率及价格变动敏感度。

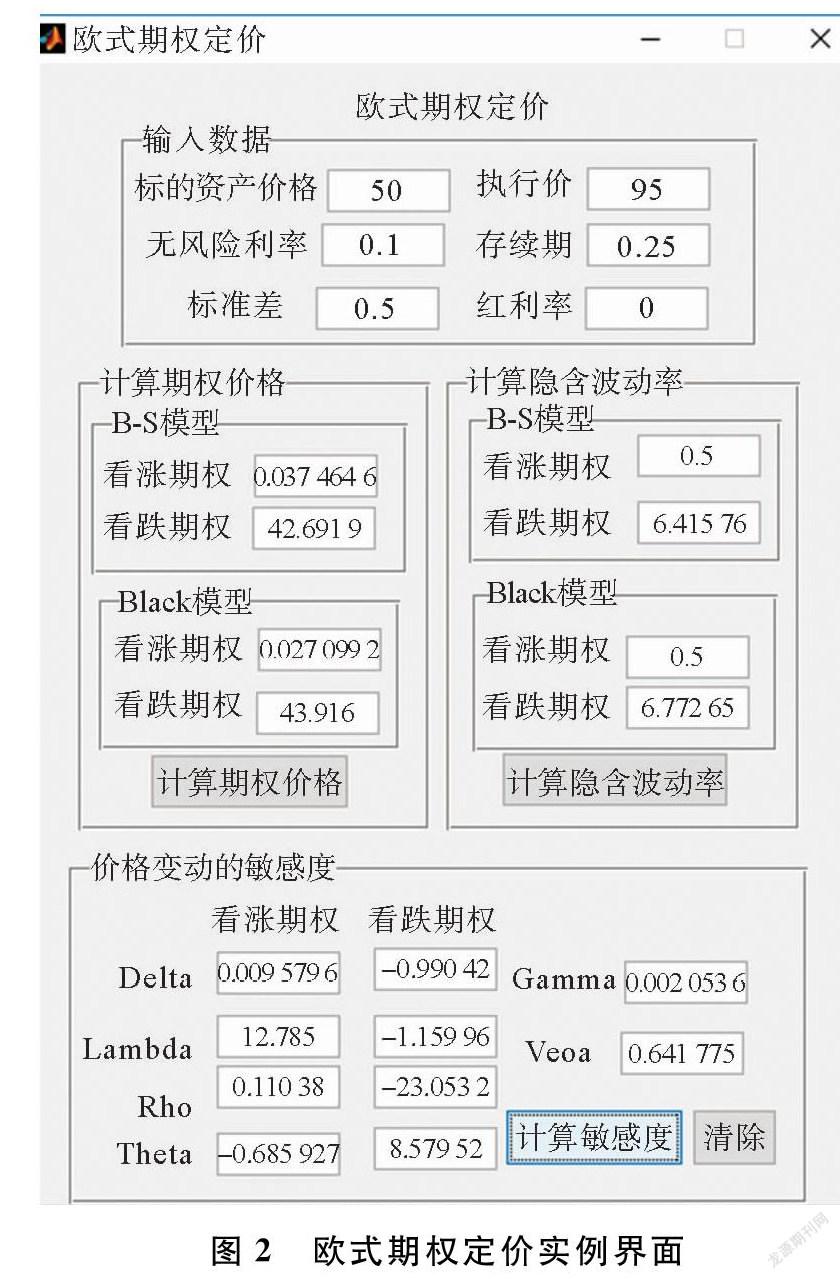
在欧式期权定价界面输入以上数据，并依次单击“计算期权价格”、“计算隐含波动率”和“计算敏感度”按钮，欧式期权定价实例界面如图2所示。

由图2可以看出，BS模型计算的看涨期权价格为0.037元，隐含波动率为0.5%，看跌期权价格为42.69元，隐含波动率为6.416%。Black模型计算的看涨期权价格为0.027元，看涨期权隐含波动率为0.5%;看跌期权价格为43.916元，看跌期权的隐含波动率为6.77%。从价格变动敏感度结果中可以看出，看涨期权的Delta为0.009 6，看跌期权的Delta为-0.99;看涨期权的Lambda为12.785，看跌期权的Lambda为-1.160;看涨期权的Rho为0.110，看跌期权的Rho为-23.05;看涨期权的Theta为-0.686，看跌期权的Theta为8.560;以及Gamma为0.002，Vega为0.642。

3.2 亚式期权定价

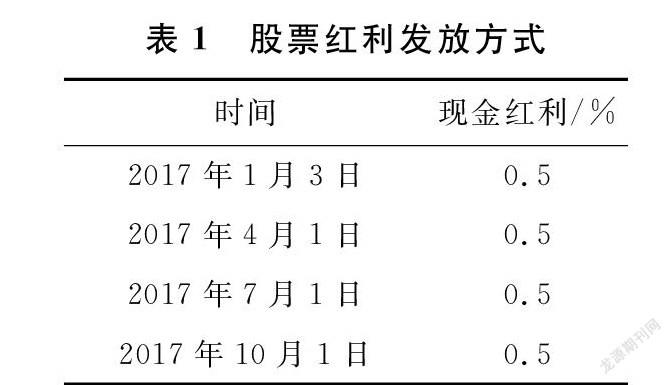
假设期权标的资产股票波动的标准差为0.2，标的资产价格为50元，红利类型为现金红利，股票红利发放方式如表1所示。国债1年期利率为5%，起息日为2017年1月1日，到期日为2017年12月31日，期权的生效日为2017年1月1日，到期日为2017年12月31日，分4段进行离散。

假设某欧式看跌亚式期权的执行价是浮动的，结算日是2017年1月1日，行权日期为2017年12月31日，计算该亚式期权价格。

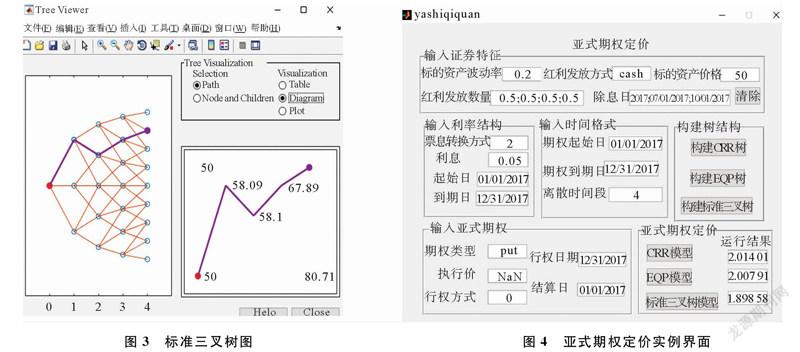
运用二叉树模型计算期权价格需要先输入标的资产的证券特征、无风险利率格式和期权时间格式来建立二叉树，再计算期权价格。先输入上述数据，再根据要选择构建的树模型，分别单击“构建CRR树”、“构建EQP树”和“构建标准三叉树”。比如要构建标准三叉树，则需单击“构建标准三叉树按钮”，在弹出的窗口中依次单击树图节点，选择一条路径，模拟标的资产价格变动情况。每个节点的数值标在路径上，标准三叉树图如图3所示。

建立树模型后，输入亚式期权数据，分别单击“CRR模型”、“EQP模型”和“标准三叉树模型”，显示不同树模型的计算结果，亚式期权定价实例界面如图4所示。

由图4可以看出，CRR二叉树模型计算的亚式期权价格为2.014元，EQP模型计算的亚式期权价格为

3.3 帽子期权定价

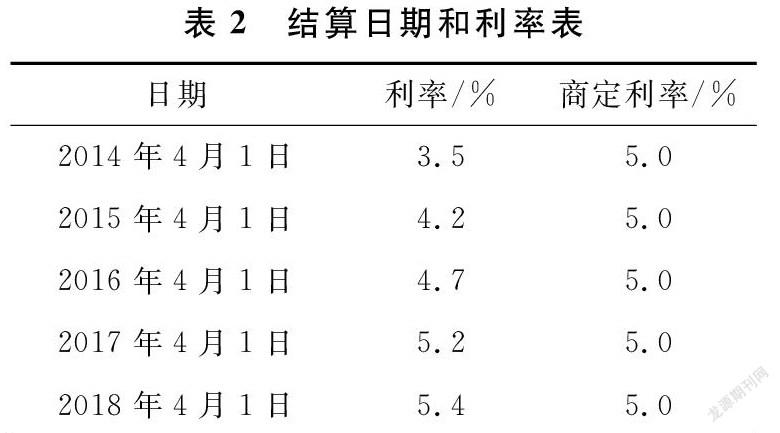
假设某公司从银行取得期限为4年的一笔贷款。该笔贷款采取浮动利率计息，这笔贷款于2014年4月1日借入，由于该公司预测利率要上升，为了规避利率上升为公司经营所带来的风险，该公司决定买入一笔期限为4年的帽子期权，商定利率为5.0%，每年结算1次，结算日期和利率如表2所示。利率波动率为0.05，均值反转日期为2018年4月1日，均值回归值为0.1，期权结算日为2014年4月1日，期权到期日为2018年4月1日，求该期权的价格和敏感性。

运用HW模型计算利率衍生品价格需要先输入利率波动格式、时间格式和利率结构的相关数据，建立HW模型的利率树结构，输入相关数据后，单击“建立HW模型利率树”，建立利率树，再输入帽子期权的相关数据，单击“计算期权价格和敏感度”按钮，可得到该帽子期权的价格和敏感度，复合期权定价实例界面如图5所示。

由图5可以看出，用HW模型计算的该帽子期权的价格为8.79元，Gamma值为-477.75，Delta值为65.78，Vega值为110.34。

4 结束语

本文通过对Matlab图形用户界面的应用，借助Matlab在数值计算、图形绘制以及可视化界面开发等方面的优势，以各类期权定价模型为理论基础，开发了期权定价系统。BS模型和Black模型计算出来的欧式期权价格较为接近，说明期权定价公式对比较简单的欧式期权定价很准确;对亚式期权定价时，两个二叉树模型和三叉树模型相比有差别，说明二叉树模型扩展成三叉树后计算精度更高;对帽子期权进行实例验证时，Delta、Gamma等值较大，说明该期权价格对利率变动较为敏感，投资者应注意风险。该期权定价系统虽然将复杂的定价模型应用于实践，但由于所用模型的局限性，并不能实现所有期权的定价，下一步研究重点是使该系统覆盖的期权品种更全面。

参考文献：

[1] 何颖俞. 美式期权的三叉树定价模型[J]. 黑龙江大学自然科学学报， 2008， 25（1）： 8184.

[2] 刘海龙，吴冲锋. 期权定价方法综述[J]. 管理科学学报， 2002， 5（2）： 6773.

[3] 刘芳，吴成就，潘俊涛. 基于Matlab/GUI的电力电子电路仿真平台构建[J]. 实验技术与管理， 2016， 33（1）： 107110，126.

[4] 孙祥，黄晓鸣. 基于MATLAB的集成化图像处理系统[J]. 科学技术与工程， 2007， 7（20）： 53865388.

[5] 年兴，朱雨婷，林剑辉. 基于SVM的股指预测模型与GUI仿真[J]. 消费导刊， 2012， 62（10）： 67， 10.

[6] 杨晓，杨德平. 基于Matlab图形用户界面的马氏链股价预测系统开发[J]. 青岛大学学报：工程技术版， 2015， 30（3）： 4349， 69.

[7] 叶志强，陈习定，张顺明. 我国定期存贷款利率期权隐含波动率研究[J]. 管理科学学报， 2011， 14（9）： 6776.

[8] 李秉祥. 对欧式期权BS模型的推广[J]. 西安理工大学学报， 2003， 19（4）： 377381.

[9] 刘春艳，吕喜明. 基于MATLAB视图的欧式看涨期权敏感性动态分析[J]. 经济论坛， 2013， 26（3）： 7176.

[10] 安占强，徐洁媛. 非正态分布下的二叉树期权定价模型[J]. 统计与决策， 2007， 22（11）： 810.

[11] 张铁. 一个新型的期权定价二叉树参数模型[J]. 系统工程理论与实践， 2000， 20（11）： 9093.