函数思想在高中物理解题中的应用

孟阔

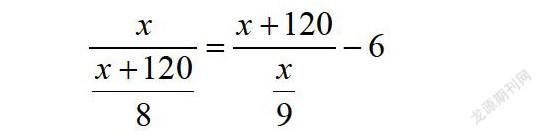
摘 要：数学知识与物理知识之间有着密切的联系，高中物理可以被认为是数学知识在现实生活中的具体应用。准确的、合理将函数思想应用于高中物理解题中，可以化繁为简，提高解题效率。函数思想在高中物理学科中的重要性不言而喻。基于此，本文对函数思想在高中物理解题中的具体应用进行了详细的探索与分析。

关键词：函数思想;高中物理;物理解题;

引言：在数学思想中，函数思想是重要的组成内容，其主要是指将非函数问题巧妙的转换为函

数表达式，并且利用函数的概念和性质去分析问题和解决问题的一种思维方式。总而言之，函数将现实世界中数量之间的关系。在高中物理解题过程中，将函数思想运用于物理题目中，将物理题目中所蕴含的数学特征进行提取，从而构建函数关系的数学题型，从而求解得到物理题目正确的答案。在运用函数思想过程中，变量是核心要素之一，也是基础和前提，函数的本质特征则为映射。通过运用函数思想，则充分体现了任何事物都是处于不断变化中的，并且这些变量之间并不是独立存在的，而是相互关联、相互影响的，寻找变量之间的关系并运用表达式正确的表达出来，有利于人们能够全面的、准确的了解事物变化的趋势以及运动规律。总之，将函数思想应用于高中物理解题中具有非常重要的现实意义。

一、高中物理解题中函数思想运用的现状分析

1.高中物理解题中学生运用函数思想缺乏积极性

实质上，高中物理学科与数学学科之间有着紧密的联系，可以认为物理学科是以数学学

科为基础的，物理是数学知识的实际应用。因此，运用数学知识去解答物理问题是非常普遍和寻常的一件事情。除此之外，物理知识体系可以被认为是从物理现象中发现规律，并提取数学联系后形成的。因此，学生在学习高中物理过程中，必须充分运用所学的数学函数的知识去积极探求物理变量中所蕴含的数学关系，构建函数表达式并进行相应的运算。但是，从目前的实际情况来看，大部分学生对于高中物理解题中运用函数思想缺乏积极性。主要原因为两方面：一方面，学生缺乏函数思想，自身数学能力水平较低，无法熟练的掌握和应用函数思想;另一方面，由于长期以来受到传统教学理念和教学模式的影响，大部分学生认为数学与物理是两门独立的学科，无法有效的运用函数思想。

2.高中物理解题中学生应用函数思想的能力水平有待提升

在高中数学学习过程中，函数这一部分的知识内容相对来说难度较大，对于学生各方面的能力水平，如逻辑思维能力、理解能力以及数学运算能力等均提出了较高的要求和标准，学生必须具备较高的基础水平才能够熟练应用函数思想。但是，在高中物理教学过程中，学生应用函数思想的能力处于较低的层次水平，学生无法从物理题目中提取有价值的信息，无法找到变量之间的关系，从而导致物理问题无法得到有效的解决。

二、函数思想在高中物理解题中应用的有效策略

1.强化学生运用函数思想解决物理题目的意识

在高中物理学习过程中，数学知识是重要的组成内容，物理学科的发展是离不开数学知识的。因此，必须让学生能够充分认识到物理学科与数学知识之间的联系，认识到函数思想在物理解题中的重要作用，强化学生的函数意识，在解决物理题目的过程中必须学会熟练运用函数思想。当学生碰到具体的物理问题时，首先应该根据相应的物理概念、规律以及原理去寻找各个变量之间所蕴含的关系，从而构建函数表达式进行求解，从而巧妙的将物理知识转化为数学问题进行求解。例如，一位身高为1.8米的运动员，他想要跳过1.8米的横杆，请问该运动员起跳时竖直方向上的分速度为多少？因此，在求解该实际问题时，第一步应该将该实际问题转换为物理问题，将运动员作为一个质点对待，并且不考虑空气阻力等因素，然后可以该运动员在竖直方向上是做匀加速直线运动，根据物理的相关概念可以构建相应的函数表达四进行求解。在很多高中物理问题中，通常会遇到二元一次线性方程组才能够进行求解，在更加复杂的情形下可能还需要构建二次方程进行求解。

2.高中物理解题中提高学生函数思想的应用能力水平

在高中物理中，处处蕴含着函数的思想，如物理原理和规律的描述、定理以及公式等方面。因此，函数思想在高中物理解题中的重要性不言而喻。对于学生而言，在学习高中物理知识过程中，必须提高自身函数思想的应用能力水平。函数思想在物理解题中的应用主要可以分为以下几种情况：

应用换元法，化难为易。在物理问题中，某些方程的求解较为复杂，具有较高的难度。在这种情形下，学生必须掌握换元法，通过合适的应用换元法，构建新的辅助变量，经常可以达到事半功倍的效果，从而降低方程求解的难度。但是，在应用换元法过程中，必须要因函数方程而定，具体问题具体对待。

例题1：甲乙两个人，分别由A、B两个地方相向匀速的前进，甲从A地出发，乙从B地出发，而且甲出发的时间要比乙晚6分钟，两人相遇时，可知乙比甲多走120米，相遇后，两人依然按照原来的速度继续前行，甲再经过8分钟到达B地，乙再经过9分钟到达目的地。请求解AB两地的距离和两人的速度。

根据题目条件，可以构建表达式：

该方程表达式求解起来较为繁琐，此时可以引入辅助变量y来替代x/（x+120）进行求解，可以大大降低求解难度，提高解题效率。

利用函数关系，寻找变化规律物理学科最鲜明的特征在于其是对物质的结构进行研究并且探寻运动的基本规律。因此，在学习物理学科过程中，必须要寻找一些可以用来描述物质结构和运动的物理量，从而寻找到物理量之间的关系，此时，一般会运用到数学上的函数关系式。因此，在物理问题中大部分的运动规律的题目求解过程中，学生均应该具备这样的意识。

第三，利用方程的根進行检验。在某些物理题目中，根据题目条件构建了一元二次方程后，求解得到的两个根均为正数，此时学生在判断时可能会存在着一定的困扰。因此，学生必须结合物理的原理和规律选择正确的答案。

三、结束语

总之，在高中物理解题中，函数思想占据着至关重要的作用。由于文章篇幅限制，仅仅只是讨论了以上三种函数思想。由此可以看出，函数思想在高中物理中应用的重要地位。

参考文献

[1]韩云霞，马旭.浅谈函数思想在高中数学解题中的应用[J].宁夏师范学院学报，2016，37（03）：92-95.

[2]王丹阳.数形结合思想在高中物理解题中的应用[J].科学大众（科学教育），2016（01）：22.