基于鲁棒连续聚类的图像超像素分割方法

庄美美 熊俊凯

（1.福建广播电视大学泉州分校，福建泉州 ，362000 ； 2.西华大学，四川成都 ，610039）

许多图像相关的算法操作的基本单元均为像素点，因而使得算法复杂度较高，同时忽略了图像整体的结构信息。超像素分割方法是根据颜色、纹理和空间位置等信息将相邻的像素点划分为像素块，后续图像处理算法以超像素作为输入就可以降低计算量并获得一定的结构信息。超像素分割算法一直作为人们研究的对象，不断有新的算法被提出。这些算法有些是在参考指标上优于目前的算法，[1]有些是生成的超像素具有不同于以往算法的特征，[2]有些是在特定的领域有着更好的应用。[3]许多超像素算法只是根据像素点的特征进行分割，但是图像作为一个整体有着更丰富的信息，将这些信息也加入到算法中就可以使得最后生成的超像素也具有更丰富的信息，使得超像素在后续的处理中得到更好的结果。为了合理地将图像的全局结构信息利用起来，本文先对已有的超像素分割算法和提取全局结构信息的方法进行了研究，再对可以在其基础上进行修改从而用于超像素分割的其他领域的算法进行了研究。经过调查和研究，最终在鲁棒连续聚类算法[4]的基础上修改得到了本文的超像素分割算法。

一、超像素分割算法

在进行像素级图像处理时往往存在两个非常大的缺点，一是如果图像包含的像素点个数很多，那么运算量就很大，甚至某些算法会不适用，二是图像自身的信息，例如图像全局结构信息或者像素点之间的关系被忽略了，这无疑就降低了图像信息的利用率。人们针对这两个缺点进行了相应的研究，提出了将图像分割为像素块再对像素块进行处理的方法。[5]直到2003年Ren等人提出了超像素的概念，[6]超像素是具有一定语义信息和结构信息的图像子区域。超像素在三维重建、[7]目标跟踪、[8]目标检测、[9]语义分割[10]和深度估计[11]等任务中都得到了很大的应用，许多算法都是基于超像素设计出来的。超像素分割算法的优劣直接关系到生成的超像素质量。目前超像素分割算法有许多的理论基础，例如分水岭、图像密度、图论、轮廓演化、聚类分析、能量优化和神经网络等等，[12]它们生成的超像素都有各自的特点。当前的超像素分割算法主要是基于图论和梯度，基于神经网络的算法也开始出现。

（一）基于图论的超像素分割算法

基于图论的算法是将图像转化为加权无向图，其中图的顶点是像素点，图的边是像素点之间的相邻关系，边的权重是像素点之间的相似或差别的量化。一般情况得到的图中所有的顶点是连接在一起的，通过算法将某些边舍去后得到若干不相连的子图，这些子图就是图像的超像素。这是一个自顶向下的图的分割，不同算法对如何分割图以及分割结果的评价是不同的。以下是一些经典的基于图论的算法：

Felzenszwalb等人提出的基于图的图像分割（Graph-Based Image Segmentation）[13]的理论基础是最小生成树，目标是使连通子图中的顶点差异尽量地小并且不同连通子图之间的差异尽量地大。该算法的运算速度较快，超像素的边界贴合度高但是形状和大小都不规则。因为作者是Felzenswalb和Huttenlocher，所以该算法也被称为FH。Shi等人提出的Normalized Cuts(NC)[14]对图进行归一化割，使得分割区域内的权重和尽量地大并且与其它区域之间的权重和尽量地小。该算法的运算速度慢，超像素的边界贴合度低，但形状和大小都比较规则。Liu等人提出的Entropy Rate Superpixel(ERS)[15]具有一个新的目标函数，它是由图上随机游动熵率和平衡项这两个部分组成，熵率部分使得超像素的结构均匀且紧凑，而平衡项使得超像素具有相差不大的像素个数。该算法的运算速度较快，超像素的边界贴合度高并且形状和大小都比较规则。

（二）基于梯度的超像素分割算法

基于梯度的算法首先是生成初始的粗糙的超像素，然后使用梯度下降法迭代的优化超像素，直到收敛。基于梯度的算法中一部分是基于聚类的，它们是在一般的聚类算法基础上进行了一些修改，将像素点作为聚类样本，像素点的颜色和空间位置等特征作为样本属性，最后得到的聚类结果就是符合超像素定义的簇。这些簇与普通的聚类结果最大的区别在于簇内的样本具有相邻关系，大多数聚类算法不会考虑到样本集或者样本之间的关系。当然在聚类时也可以加入一些辅助信息或者约束条件，使得生成的超像素更符合预期的要求。Simple Linear Iterative Clustering(SLIC)[16]是一种经典且流行的基于聚类的算法。

Achanta等人提出的SLIC是基于K-means[17]算法修改而来的。该方法将彩色图像的RGB颜色空间转换为CIELAB颜色空间，再结合空间位置XY得到5维的特征向量。然后利用特征向量进行聚类并且将与聚类中心在图像上相距大于一定距离的像素点直接排除。该算法的运算速度快，能够生成具有均匀紧致的超像素区域。

二、鲁棒连续聚类

鲁棒连续聚类算法主要是针对目前聚类算法在处理高维数据时效果不理想、在处理不同的域和数据集时需要相应的调整算法参数以适应不同数据的特点这两个问题而设计的。它是一种跨域聚类算法，可以有效地处理高维数据和大数据集，具有较高的聚类精度。该算法在经过拓展之后还可以实现聚类和降维的联合。由于该算法将聚类表示为基于鲁棒估计的连续目标优化，因此作者将其称为robust continuous clustering (RCC)。而通过拓展RCC达到联合执行聚类和降维的拓展算法被称为RCC-DR，它学习将高维数据嵌入到一个低维空间中，并在其中进行聚集。

RCC不会直接对数据集X=[x1,x2,…xn]进行操作，而是在一个表征集U=[u1,u2,…un]上进行操作，其中X和U中的每个样本都是D维数据。U使用X进行初始化，基于U的优化 操作揭示了数据集中的潜在集群结构。RCC的目标函数如下：

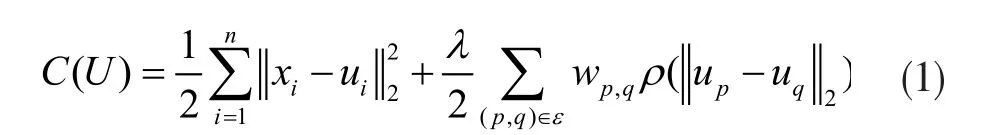
其中ε是由数据点构成的图的边的集合，RCC使用了mutual k-nearest neighbors (m-kNN)[18]算法生成边。权重wp,q根据ε得到，代表p和q两个样本的相似度。λ平衡了函数内不同项的强度。p(.)是正则化的惩罚项，为了使来自同一潜在簇的ui崩溃成一个点选取了10范数，但是也使得优化变得困难，而11和12范数不能处理ε中的伪边，最后选择了Geman-McClure估计器。可以将该式子理解为在使得U与X尽量的相似的同时使得权重wp,q大的成对项up和uq也尽量相似，即在优化操作U时避免与原始数据相差过大并且将近似的成对数据点划分到同一类。

为每个连接(p,q)∈ε引入了一个辅助变量lp,q，并优化U和L=｛lp,q｝的联合目标：

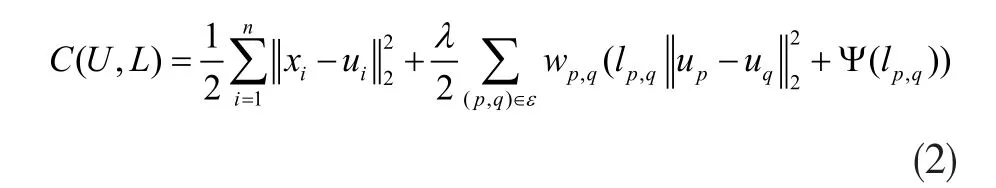
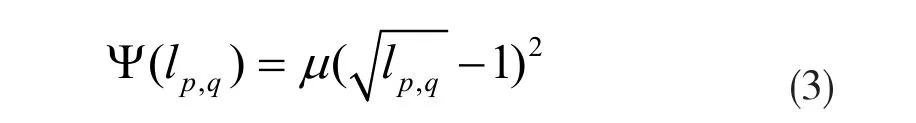
其中μ是尺度参数。

使用交替迭代来优化目标函数，当U固定时可用以下公式求解lp,q：

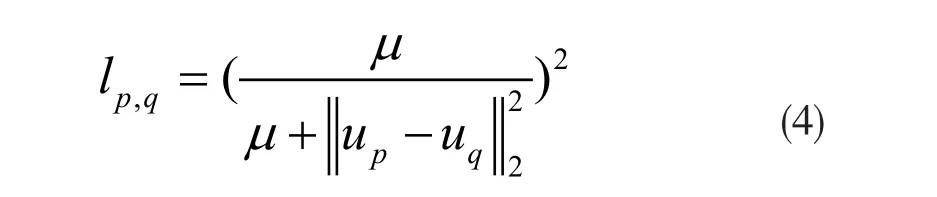
当lp,q固定，可以重写公式2，得到求解U的公式：

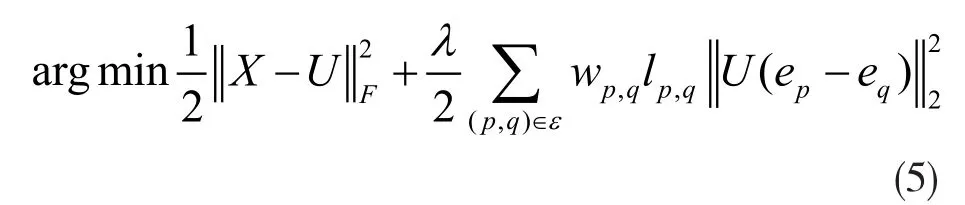
其中ei是一个指示向量，第i个元素设为1。这是一个线性最小二乘问题，线性最小二乘公式是：

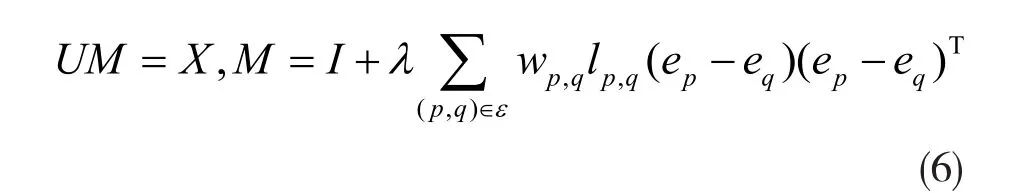
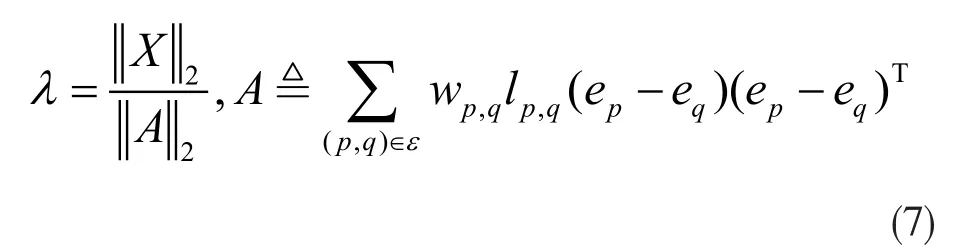
三、基于鲁棒连续聚类的超像素分割算法

?

四、实验

本文的实验平台是MATLAB，实验数据库是BSDS500。对大量的图像进行分割后可以看出本文算法可以生成贴合边界的超像素，但是超像素的形状较为不规则并且大小相差较大。这主要是由于加入了含结构信息的邻接表，并且在本文算法中邻接表起到了很大的作用，所以分割的结果会更贴合边界并且形状不规则。同时，本文算法中没有对超像素的大小进行约束并且像素的空间位置特征起到的作用不大，所以会产生较大或较小的超像素。本文算法同Ncut，Linear Spectral Clustering(LSC) ，[19]SLIC和FH这几个经典算法进行了对比，结果如图1所示。本文算法中RCC的最大迭代次数是100，内循环次数是4。LSC中ratio=0.075。SLIC中颜色和空间位置的平衡项值是20。FH中sigma= 0.5，kappa = 32，Nsup=270。Ncut，LSC和SLIC的超像素个数是60。从中可以看出本文算法比FH，Ncut和SLIC等算法更贴合边界，能够更精确的分割出贴合图像边界的超像素，尤其是其它算法分割不出来的弱边界。最贴合边界的是LSC，但也因此在一些边缘复杂的图像上分割的超像素边界较为杂乱。例如图1第三行中鸟的头顶。

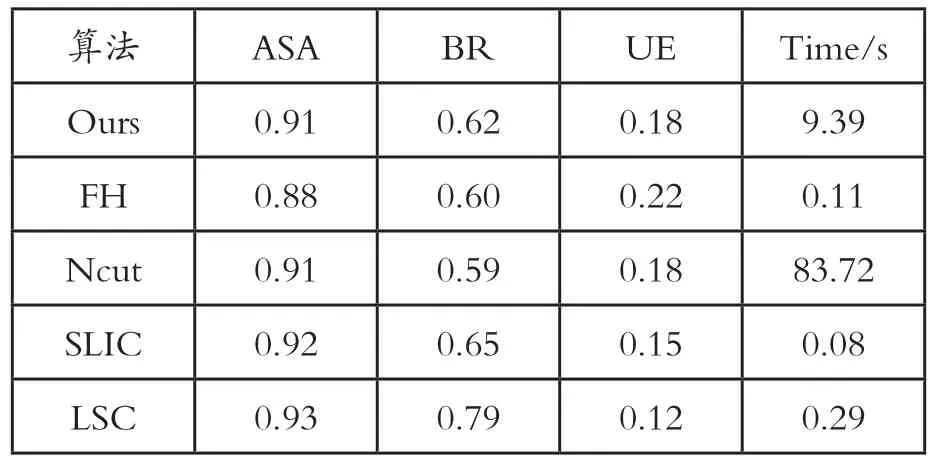
表1 不同算法的指标对比Tab. 1 Index comparison of different algorithms

由于基 于RCC算法，本文算法不可以指定超像素的个数，所以不能有效地与其它的超像素分割算法进行各项指标上的对比。为了得到比较客观的结果，取本文算法分割后的超像素个数的平均值60作为参考，用60作为指定的超像素个数用于对比算法。但是FH也是不能指定超像素的个数的，所以在实验时通过调整参数使得FH分割得到的超像素个数的平均值与本文相同也是60。所有算法的参数和上文相同。本文在achievable segmentation accuracy (ASA)，Boundary recall (BR)，undersegmentation error (UE)以及运行时间等指标上进行了评估，实验结果如表1所示。本文算法结合了图像边缘信息，分割出的超像素更加贴合边界但是这些边界可能更多的是背景边界，所以在BR上较好但不突出。同时由于本文算法分割出的超像素形状较为不规则并且大小相差较大，所以在ASA和UE上存在不足。

图1 分割结果，(a)本文算法，(b)FH，(c)Ncut，(d)SLIC，(e)LSCFig． 1 Segmentation results, (a) Ours, (b)FH, (c)Ncut, (d)SLIC, (e)LSC

五、结论

本文提出了一种基于鲁棒连续聚类算法的图像超像素分割方法，可以有效地分割出具有较高边界贴合度的超像素。其中，图像的边缘经过转换后作为本文算法的输入，提供了全局结构信息，并且在运算中起到了重要的作用，决定了最终生成的超像素的特点。可以看出图像的全局结构信息可以辅助超像素的分割，使得超像素的边界贴合度提升。但是对于背景占主要部分或者边界复杂的图像而言可能反而使得分割结果变差，需要在算法中进行平衡。