煤矿采空区稳定性分析与研究

安文伟

（山西西山煤电股份有限公司西曲矿 ，山西 古交030200）

0 引 言

煤炭作为我国现阶段主要的能源资源，对国民经济的发展、经济的高效快速增长具有重要的影响。现有的研究资料表明，我国煤炭资源储存量丰富，在石化能源中占比高达94%[1]。虽然近年来其它新能源利用比率不断提升，但在目前及今后一段时间内，煤炭仍将对国民经济的发展起着极其重要作用[2-4]。在煤炭开采完成后，会出现许多空腔和空洞，形成规模不一的采空区。采空区的形成不仅对煤矿安全开采造成极大危险，也会对地面的建筑物、工程等造成潜在危害。因此，对煤矿采空区的准确探测，了解和掌握采空区及周边的地质构造、岩层特征，确定采空区的深度大小、状态等基本信息显得尤为重要。

1 煤矿采空区的地质特征

煤矿采空区会对原有的地质结构产生影响，采空区地基原有的应力平衡被打破，由此引发采空区塌陷和持力层破坏等地质问题。煤炭采空区的类型可分为空洞型和塌陷型两类[5]，空洞型主要是由采煤过程中各种巷道的掘进形成的；塌陷型采空区主要是由于大面积的采煤引发的煤层及上覆岩层塌陷造成的，主要由三部分组成：沉降带、裂隙带、冒落带。

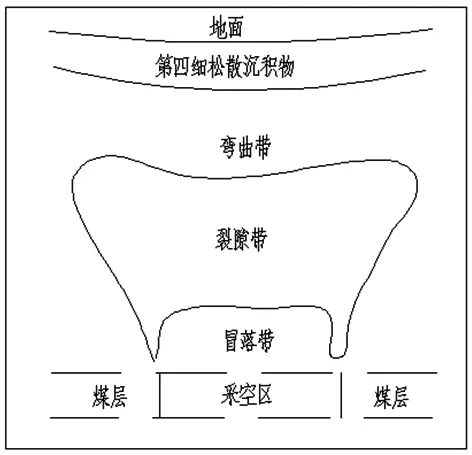
图1 采空区三带结构图

冒落带上层通常为脆性岩，当下部煤矿开采完成后，脆性岩层发生塌落，回填到采空区域，形成冒落带；裂隙带位于冒落带上部，岩层主要在脆性与塑性之间，当冒落带发生崩落后，裂隙带发生不完全塌落，主要是由于其横向应力大于竖向应力，岩层发生大量变形，形成裂隙；沉降带位于最上层，主要以塑性岩层为主，受下部岩层变化，沉降带也发生了下沉，但没有塌落，岩层性质没有发生根本变化，其变形特点为下部变形大，范围小；上部变形小，范围大。

2 采空区稳定性分析与评价

2.1 采空区稳定性影响因素

影响采空区稳定性四大因素为[6-7]：地质因素、水文因素、环境因素和工程因素，造成采空区塌落的原因是上述因素的随机共同作用结果。其中地质因素主要包括岩体结构、岩石性质以及岩石的RQD质量指标；水文因素主要对岩体产生力学作用和物理作用，它与岩体相互作用，在改变地下水自身物理、力学性质的同时改变了岩体的物理、化学及力学性质；环境因素主要包括相邻采空区以及上覆松散堆积层的影响等；工程因素主要考虑采空区的埋藏深度和采空区面积的影响，一般情况下，采空区埋藏深度越深，顶板暴露面积越大，稳定就越差。

2.2 采空区顶板厚度的计算

采空区顶板承受着采空区上部所有载荷，因此采空区顶板稳定性对采空区稳定性具有重要作用。本文通过不同方法对采空区安全厚度的合理值进行分析。分析过程中顶板岩层密度取2.36g/cm3，单轴抗压和抗拉强度分别为6.1MPa和0.34MPa,内摩擦角为36.5°，凝聚力为 0.6MPa,外部载荷q=0，安全系数K=1.5。

1）厚跨比法。

厚跨比法认为当采空区顶板厚度与顶板跨度的比值大于0.5时，即认为采空区顶板是安全的，得出计算公式如下：

式中：K为安全系数；W为采空区顶板的跨度，单位m；H为采空区顶板安全厚度，单位m。

2）载荷传递线交汇法。将顶板上方载荷简化为一条与竖直方向呈30°-35°的传递线，通过与顶板与洞壁交点进行对比，若传递线在交点外侧，则认为洞壁可以承受顶板上外载荷及岩石自重，顶板是安全的。顶板安全厚度计算公式为：

式中：θ为扩散角，去θ=32°；b为采空区跨度，单位为m；H为采空区顶板安全厚度，单位m。

3）普氏拱理论法。

此计算方法的前提是采空区在发生破坏前处于自然平衡状态，上部岩体及外载荷全部由拱承担，即采空区要形成自然压力拱。为了形成自然压力拱，采空区上方必须要有足够厚度的稳定岩层，本次计算中取稳定岩层厚度等于压力拱拱高厚度：

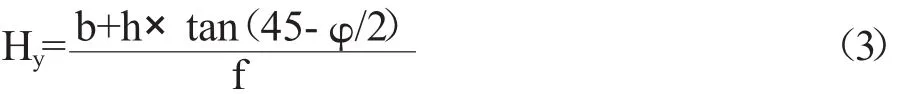
式中：Hy为压力拱拱高，单位为m；Φ为内摩擦角，取φ=36.5°；h为采空区最大高度，取h=15m；b为采空区跨度一半，单位为m；f为顶板岩层强度系数为单轴抗拉强度，单位为MPa）。

4）K.B.佩鲁涅伊特法。

在综合考虑岩体强度、地质特征、采空区跨度、作业设备等因素的基础上，根据叠加原理和独立作用原则，根据顶板最大拉应力计算得安全厚度，其计算公式如下：

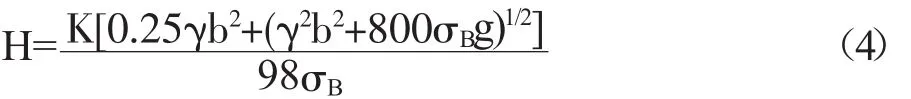
其中：H为采空区顶板安全厚度，单位m；K为安全系数；γ为顶板岩层容重，单位为kN/m3；采空区跨度，单位为m；σB为顶板强度极限；g为设备对顶板压力，取g=0，单位为MPa;

5）结构力学梁理论法。

将采空区顶板两端视为固定端，上部受岩层自重及外载荷作用，顶板按照受弯梁进行考虑，岩层抗拉强度作为控制指标，安全厚度的计算公式如下：

其中：H为采空区顶板安全厚度，单位m；γ为顶板岩层容重，单位为kN/m3；b为采空区跨度，单位为m；g为设备对顶板压力，取g=0，单位为MPa；ln为采空区宽度，单位为m；σt为单轴极限抗拉应力，单位为kPa；

2.3 采空区稳定性分析

图2 空区跨度与顶板安全厚度之间关系图

根据上述不同方法计算得不同采空区跨度对应采空区顶板安全高度如图2所示。

从图2可以看出，五种计算方法计算结果较为一致，其中厚跨比法和载荷传递交汇法具有明显的线性性质；结构力学梁理论法和K.B.佩鲁涅特法考虑因素较多，两者的曲线变化趋势较为接近。

3 采空区数值模拟

根据现场实测数据，参照已有资料，选取地层物理参数主要值见表1。

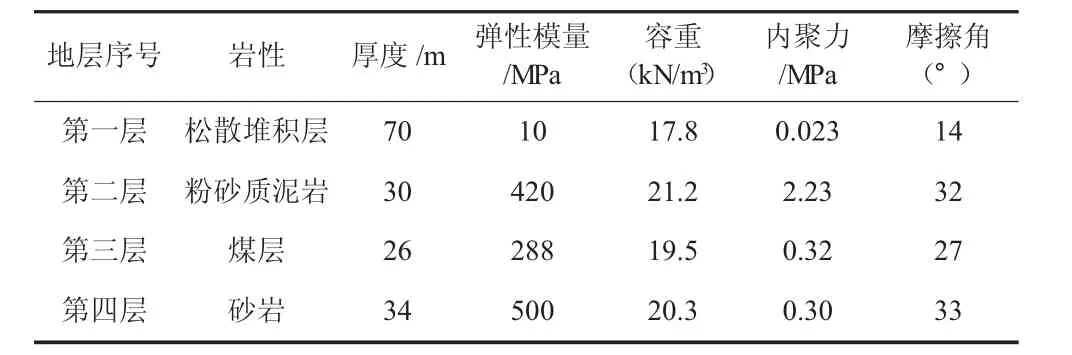
表1 模拟地层主要物理参数表

本文通过采用三维离散单元法软件FLAC3D建立采空区模型，在综合考虑模型边界效应的影响以及工作面各围岩特性的基础上，设置模型大小为长150m×宽10m×厚160m，取重力加速度g=9.81m/s2，该场地松散堆积物厚度约为70m，岩层厚度30m，煤层厚约26m；模型底边界定位全约束边界，上边界定位自由边界，地基自重应力为模型的初始应力，图3所示为数值计算模型图。

图3 数值模拟计算模型图

图4 、图5所示为采空区开挖后水平位移和垂直位移云图，从图可以发现，采空区在煤层开采完成后，采空区周边发生了明显变形，主要产生在采空区上部两侧及采空区两端，采空区水平位移量最大值发生在其上部，位移量为2.82cm；在顶板发生沉降后，其竖向最大位移量达36.8cm。

图6、图7所示为采空区开挖后最大最小主应力图，从图可以发现，采空区底板由于在煤层开挖后出现上隆，而顶板在外载荷作用下下沉，使得主应力最大处发生在采空区角点处，应力集中较为明显，并且以压应力为主，最小值为-6.71×106Pa，最大主应力为-1.42×106Pa。

图4 采空区开挖水平位移云图

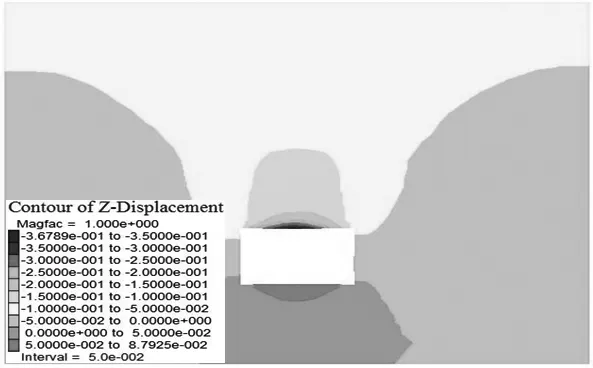
图5 采空区开挖垂直位移云图

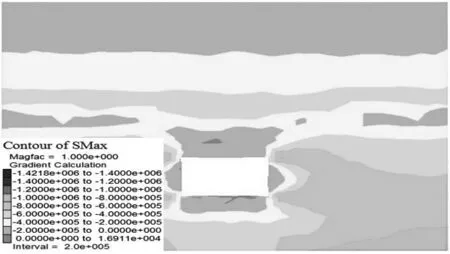
图6 采空区开挖最大主应力图

图7 采空区开挖最小主应力图

4 结 语

本文通过对采空区形成机理进行研究，并用不同方法对采空区顶板安全厚度进行了分析计算，其中厚跨比法和载荷传递交汇法具有明显的线性性质；结构力学梁理论法和K.B.佩鲁涅特法因考虑因素较多，两者的曲线变化趋势较为接近，分析对比后提出了不同跨度对应的顶板厚度值。在应用FLAC3D数值模拟分析后发现，煤层采空区角点处应力集中较为明显，并且以压应力为主，通过仿真结果得出顶板最大位移量，从而为采空区稳定性的研究提供依据。