曲线钢混凝土组合梁桥负弯矩区受力影响参数研究

张 海，张敬轩，孙 潭

(沈阳建筑大学 交通工程学院 沈阳市 110168)

曲线梁桥线型优美，跨越能力强，桥梁的平面布置能完美地符合公路线型；钢-混凝土组合结构自重较小，构件截面尺寸小，可以有效增加承载力，降低工程造价，缩短施工周期，并且可以增加构件与结构的延性[1]。曲线组合梁是将这两种结构组合在一起，充分发挥两种结构的优势[2]。对于曲线组合梁桥分析与计算时，负弯矩区是其计算的重点，从负弯矩区的荷载-位移曲线与开裂弯矩两方面进行分析，分别通过控制预应力、曲率半径、混凝土板强度三个参数分析其对于负弯矩区受力的影响。

1 模型实例

1.1 模型参数

选取一两跨超静定曲线钢-混凝土组合箱梁进行分析，梁的具体参数如下：曲率半径R=180m，梁弧长L=30m，其中第一跨跨长L1=15m，第二跨跨长L2=15m，混凝土板宽b=6m，板厚hc=0.24m，翼缘板长度b1=1.5m，钢箱梁高度hs=1.8m，钢箱梁底板宽度b3=2m，钢腹板厚度ts=0.02m。截面形式，见图1[3]。

图1 曲线钢与混凝土组合箱梁截面图

1.2 建立模型

拟采用实体单元用于模拟钢筋混凝土翼缘板，平面板单元模拟钢箱梁及加劲肋，剪力连接件采用梁单元进行模拟，采用连接单元模拟横隔板[4]，增强桥梁横向刚度。

对于混凝土板，采用总应变裂缝模型来模拟混凝土构件的材料非线性破坏[5]。对于混凝土的受压硬化-软化函数采用Thorenfeldt函数，对于混凝土受拉硬化-软化函数采用常量函数。

将钢箱梁作为理想弹塑性材料进行模拟，开孔钢板的屈服强度为fy=345MPa。当开孔钢板应力达到屈服强度后，应力应变为斜率为0的曲线。在有限元软件中对其采用Von Mises模型硬化函数进行定义[6]。

取预应力为450kN、550kN、650kN、750kN，建立GH1-GH4模型；取混凝土强度为C45、C50、C55、C60，建立GH5-GH8模型；取曲率半径为50m、75m、100m、300m，建立GH9-GH12模型。

建立典型模型如图2所示。

图2 梁体模型图

2 荷载-位移曲线

在同一半径方向上采集2个节点，外箱节点号为3096，内箱节点号为1057。绘制预应力由小到大全过程荷载-位移曲线。

2.1 预应力

图3 不同预应力的外侧、内侧荷载-位移曲线

由图3可以看出：

(1)在荷载为0.75时，GH1、GH2、GH3、GH4的外侧挠度值为13.52mm、11.58mm、10.11mm、8.96mm，预应力对于结构位移具有很好的限制作用，从而起到提高结构整体刚度的作用。

(2)随着荷载的逐渐增大，箱梁外侧的挠度始终大于内侧。在预应力逐渐增大的过程中，都具有这个规律，这很好地模拟了曲线梁桥明显不同于直线梁桥的特点。

2.2 混凝土强度

图4 不同混凝土强度等级的外侧、内侧荷载-位移曲线

图4反映了GH5～GH8在混凝土强度等级分别为C45～C60时的荷载-位移曲线，从开始加载到曲线最高点，各试件曲线斜率相近，表明提高混凝土强度等级对组合梁刚度的影响不大。在相同荷载作用下，随着混凝土强度等级的提高，自由端的挠度并没有得到显著的控制。说明提高混凝土强度等级对于降低自由端挠度没有起到有效的控制作用。

2.3 曲率半径

(1)当曲率半径为100m以上时，在相同荷载作用下，随着曲率半径的增大，自由端的挠度并没有明显的降低，说明此时已接近直线梁的受力特性，对组合梁的整体刚度不会产生较大影响。

图5 不同曲率半径的外侧、内侧荷载-位移曲线

(2)当曲率半径为100m以下时，在相同荷载作用下，随着曲率半径的增大，自由端的挠度降落幅度较大，说明提高曲率半径会提高组合梁的整体刚度。

3 开裂弯矩

取外箱节点号为3096，内箱节点号为1057，取其内外侧开裂弯矩值，绘制柱状图。

3.1 预应力

表1 箱梁内、外侧开裂荷载(单位：kN·m)

图6 箱梁内、外侧开裂弯矩对比图

从表1、图6中可以看出，曲线箱梁顶腹板连接处外侧先于内侧开裂，随着预应力的提高，开裂弯矩最大提高30%，施加预应力后显著地改善了钢-混凝土组合梁负弯矩区的抗裂性能。

3.2 混凝土板强度

由表2、图7可以看出，箱梁内、外侧的开裂弯矩不同，外侧要先于内侧开裂。这反映了曲梁的特性。随着混凝土强度等级的提高，开裂荷载最大只提高了10%，说明提高混凝土强度等级对于提高开裂弯矩效果不明显，虽然开裂荷载与混凝土的强度等级有着密切的联系，但是，从模拟试验结果得知，提高混凝土强度等级并不能很好地推迟开裂荷载，在工程实际中，根据具体问题具体对待，因为每提高一个混凝土强度等级要耗费大量的资金，因此，应该选用经济又实惠的一种，这样，既可以降低工程造价，又可以使混凝土的性能得到很好的发挥。

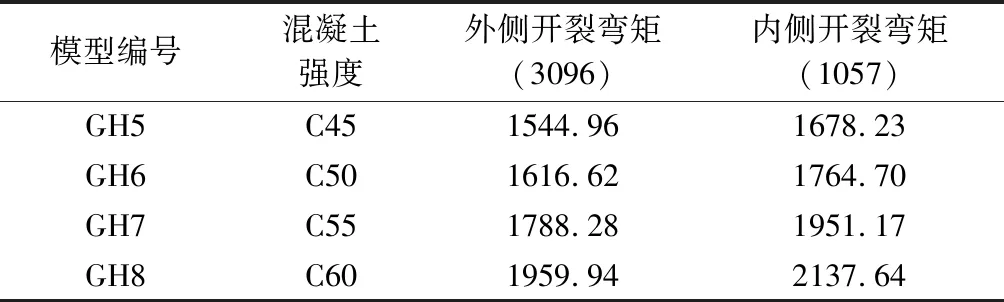
表2 箱梁内、外侧开裂荷载(单位：N·m)

图7 箱梁内、外侧开裂弯矩对比图

3.3 曲率半径

从表3、图8中得出，内、外侧开裂弯矩不同，外侧要先于内侧开裂，这反映了曲梁的特性，随着曲率半径的提高，当曲率半径小于100m时，开裂荷载提高幅度明显，最大提高24%；当曲率半径大于100m时，开裂荷载提高不明显，最大仅提高3%。可以得知，对于小半径曲线组合梁桥，提高曲率半径可以推迟开裂荷载。

表3 箱梁内、外侧开裂荷载(单位：kN·m)

图8 箱梁内、外侧开裂弯矩对比图

4 结语

通过改变预应力大小、混凝土板强度、曲率半径这三个参数，获知其对于荷载-位移曲线以及开裂弯矩的影响，其对于荷载-位移曲线的影响为：

(1)预应力对于荷载-位移曲线影响显著，可以有效控制自由端挠度；混凝土强度对于荷载-位移曲线基本无影响；曲率半径小于100m时，提高曲率半径可以有效减小自由端挠度，大于100m时，提高曲率半径无显著影响。

(2)由内外侧荷载-位移曲线可以看出，外侧挠度大于内侧，这是曲线梁明显不同于直线梁的特点。

其对于开裂荷载的影响为：

预应力对于开裂荷载影响显著，最大可使开裂弯矩提高30%；混凝土强度等级对于开裂荷载影响较小，最大提高开裂弯矩10%，性价比低；曲率半径小于100m时，对开裂荷载影响显著，最大可使开裂弯矩提高24%，曲率半径大于100m时，对于开裂荷载的提高较小，最大仅提高3%。