红黏土固结-蠕变特性及其耦合模型*
2019-09-06陈昌富朱世民毛凤山张根宝
陈昌富 朱世民 毛凤山 张根宝
(①湖南大学建筑安全与节能教育部重点实验室 长沙 410082)(②湖南大学土木工程学院 长沙 410082)
0 引 言
红黏土广泛分布于我国南方水量充沛的湿润地区,其蠕变特性与长期稳定性直接关系到工程本身以及周边环境的安全,因此开展红黏土蠕变特性研究具有重要的工程意义。
岩土蠕变特性通常采用元件蠕变模型和经验蠕变模型来描述。比较著名的元件模型有:Maxwell模型、Kelvin模型、Burgers模型等; 比较著名的蠕变经验模型有:Singh-Mitchell模型(Singh et al.,1968)、Mesri模型(Mesri et al.,1981)等。詹美礼等(1993)将双屈服面弹塑性模型与软土的流变性相结合,建立了一个带有双屈服面的流变模型; 卢萍珍等(2008)提出了一个新的蠕变经验模型,该模型与试验结果拟合效果良好; 赵明华等(2004)对西原模型进行了改进,并通过室内直剪蠕变试验验证了模型的合理性; 陈昌富等(2008,2016)还建立了海相软土的改进BP神经网络蠕变本构模型和锚-土界面的剪切蠕变经验模型; 此外,刘德方等(2017)依据双曲线模型建立了不同含水率下的EPS颗粒轻量土经验蠕变模型; 陈晓雪等(2017)建立了纤维加筋膨胀土的Mesri蠕变模型。
作为国内岩土流变学的主要奠基人,陈宗基(1958)最早将流变模型与固结理论结合起来研究土体的变形; 赵维炳(1989)采用广义Voigt模型,导出了饱和土一维流变固结问题的普遍理论解; 陈晓平等(2003)将Duncan非线弹性模型与Kelvin模型相串联,并将其引入到Biot固结理论中,以此建立了固结-蠕变耦合模型; 孙明乾等(2015)对Singh-Mitchell模型进行修正,并利用修正后的Singh-Mitchell模型建立了考虑软土流变特性的一维及三维固结流变微分方程。
如果能将固结理论与蠕变模型结合起来,这样在分析红黏土受力变形的时间效应时,便能够同时考虑固结和蠕变这两种因素的影响,这对进一步认识红黏土的工程性质是很有意义的。
本文利用设计改制后的三轴蠕变试验装置,对红黏土试样进行室内排水三轴蠕变试验,得到蠕变全过程曲线及其蠕变破坏阈值; 然后根据部分应力水平下的蠕变试验结果建立出考虑固结-蠕变耦合作用的红黏土元件蠕变模型; 最后利用所建模型对另一部分蠕变试验结果进行预测,以验证模型的精准度。
1 红黏土三轴蠕变试验
1.1 试验用料及装置
试验所用土料取自湖南省长沙市宁乡县某高速路段,其主要的物理力学参数如表 1。

表 1 红黏土的基本物理力学参数Table 1 Properties of red clay used in testing
试验装置采用自行设计改制后的TSZ应变控制式三轴仪,该装置主要由加载系统和数据采集系统构成,具体构造如图 1。

图 1 三轴蠕变试验装置Fig. 1 Tri-axial creep testing device
1.2 试验方法
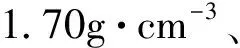
本文试验中的蠕变加载方式为分级加载,即在同一个试样上逐级施加不同的荷载,待该级荷载作用下的变形稳定或者达到预定时间后再施加下一级荷载,直至试样产生破坏(孙钧, 1999)。根据各平行试样固结不排水三轴压缩试验破坏偏应力的大小,将加载等级分成6~9级。选用的蠕变稳定标准为10i000is内变形量小于0.01imm(孙钧, 1999)。由于试验用料为红黏土,击实后的土样受力后变形能在24ih内达到稳定标准,鉴于此,每级荷载的施加时间为24ih。
1.3 试验结果
对在200ikPa围压下固结完成的红黏土试样进行分级加载,得到分级加载全过程曲线(图 2)。
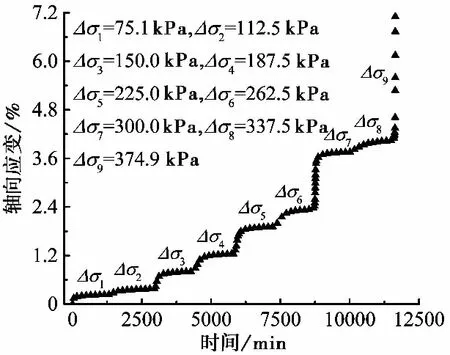
图 2 红黏土三轴蠕变分级加载全过程曲线Fig. 2 Stepwise loaded full-process creep curve of red clay
采用“陈氏加载法”(陈宗基等, 1991)对分级加载全过程曲线进行处理,可得到分别加载条件下的轴向应变-时间关系曲线(图 3)。

图 3 红黏土三轴蠕变分别加载曲线Fig. 3 Individual creep curves for varying stress levels
在图 3中t=0.5ih、1ih、2ih、3ih、6ih、12ih、18ih、24ih处作平行于纵轴(轴向应变)的直线与各级蠕变曲线相交,根据各交点的轴向应变和偏应力值绘出偏应力-轴向应变等时曲线(图 4)。将各等时曲线屈服极限值的连线所组成的水平渐近线在偏应力轴上的截距作为红黏土蠕变破坏阈值,于是可得该土样的蠕变破坏阈值:Δσf=300.0ikPa。
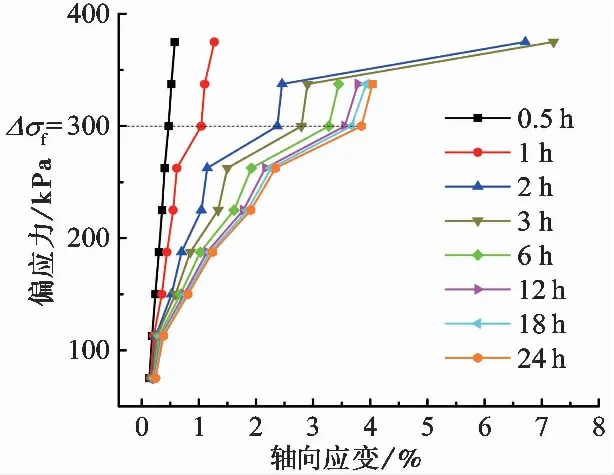
图 4 偏应力-轴向应变等时曲线Fig. 4 Isochronal curves for deviatoric stress-axial strain
由图 2、图3可知,在偏应力较小时,蠕变处于衰减阶段,试样的轴向应变在初期增长很快,随后应变增长的速率逐渐变小,最终趋于稳定。此外,在偏应力较大时,加载初期一定时间范围内会出现明显的应变增长迟滞的现象,对应在分别加载曲线上存在两个较为明显的拐点,这与杨超等(2012)所进行的三轴排水蠕变试验的结果相似,该文用“Mandel-Cryer”效应解释了这一现象。
2 红黏土固结-蠕变模型
2.1 分别加载下固结-蠕变模型
红黏土试样在围压σ3作用下固结完成后、开始施加偏应力Δσ时便同时开始监测试样的竖向变形,并以此作为本文模型的初始点(t=0)。这样,试样在偏应力Δσ作用下产生的竖向变形所对应的应变是瞬时应变εd、固结应变(偏压固结产生的应变)εc以及蠕应变εs的总和:
ε=εd+εc+εs
(1)
其中,瞬时应变εd在偏应力Δσ施加的瞬间便已产生,固结应变εc与蠕应变εs与加载时间有关,并在初始点t=0时为0。
由以上分析可知,本文模型的边值条件为:t=0时,孔隙水压力u=0,σ1=σ3+Δσ,σ2=σ3,ε|t=0=εd。下面分别对瞬时应变εd、固结应变εc以及蠕应变εs的计算方法展开讨论。
利用弹簧元件描述土体受力产生的瞬时应变:
(2)
式中,E0为初始模量。
假定试样内部的应力分布是均匀的,则固结应变的总量为:
(3)
式中,εc为固结应变的总量;Es为土的压缩模量。
引入曾国熙等(1959)提出的平均固结度统一表达式:
(4)
式中,α、β为与排水条件相关的待定参数。
土体在某一时刻下固结应变的大小即为土体固结应变的总量与平均固结度的乘积:
(5)
蠕变变形可分为衰减蠕变(变形最终趋于稳定)和加速蠕变(最终发生破坏)两个阶段,本文仅讨论衰减蠕变模型的建立。采用由弹簧元件与黏壶元件通过并联组合而成的Kelvin模型(图 5)来描述红黏土的蠕变特性,即:
(6)
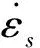

图 5 Kelvin模型Fig. 5 Kelvin model
求解式(6)并代入初始条件,即可得到蠕变方程:
(7)
试验结果(图 2、图3)表明:红黏土在受力后产生应变,但是其应变增长存在一定时间的迟滞。鉴于此,引入蠕变迟滞时间t0这一参数,即时间t=t0时红黏土才开始出现蠕变变形。引入开关函数
(8)
然后将蠕变迟滞时间t0及开关函数
(9)
将式(2)、式(5)和式(9)代入式(1)即可得到考虑固结-蠕变耦合作用的红黏土元件蠕变模型(图6):

(10)
式中,蠕变迟滞时间t0、固结参数α和β、初始模量E0、压缩模量Es、弹性模量Ek以及黏滞系数ηk为7个模型参数,其值均可由试验结果回归得到。
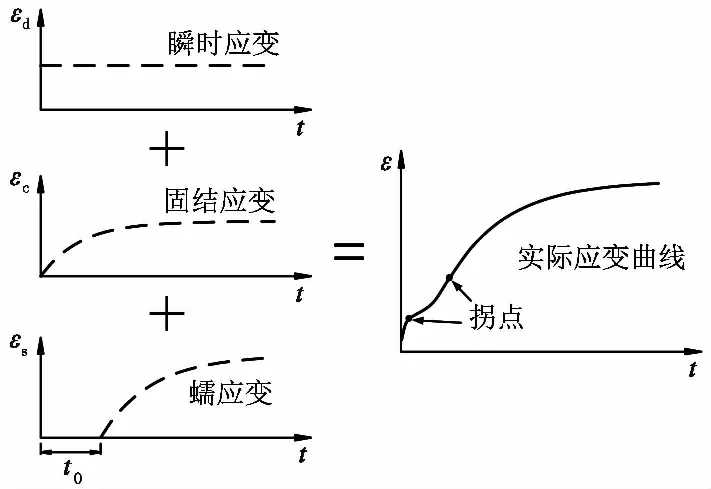
图 6 考虑固结-蠕变耦合作用的红黏土元件蠕变模型Fig. 6 Element creep model characterizing creep behavior coupled with soil consolidation for red clay
2.2 模型参数的确定及模型建立
将偏应力水平分别为Δσ1、Δσ2、Δσ3、Δσ4、Δσ6和Δσ8所对应的衰减蠕变曲线用式(10)进行回归建模,拟合结果如图 7所示,得到各模型参数值如表 2所示。图 7表明:本文模型对试验结果的拟合效果良好。
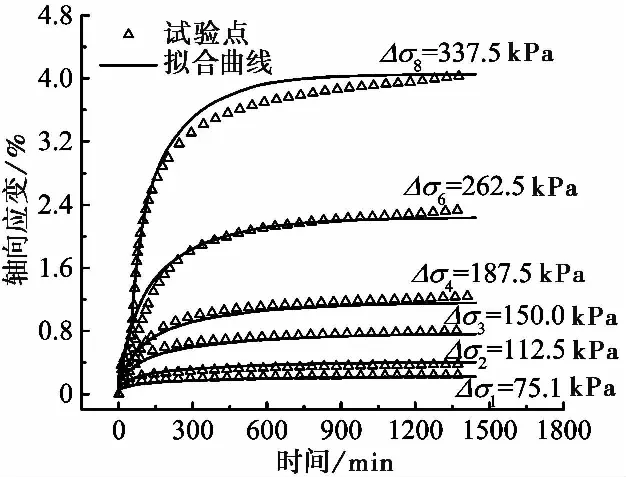
图 7 本文模型对蠕变曲线拟合结果Fig. 7 Fitted creep curves by using the presented model
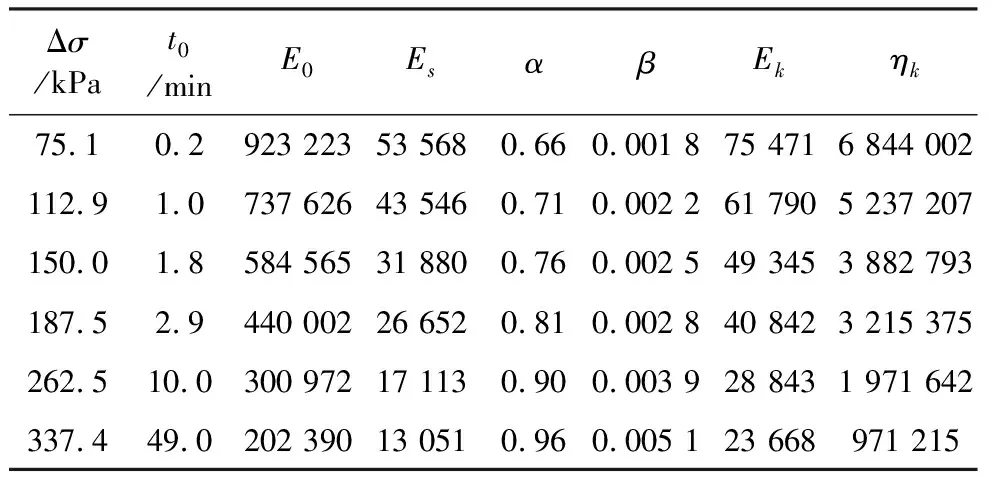
表 2 各模型参数值Table 2 Values of parameters for the presented model
由图 7和表 2可知:模型参数t0、α、β、E0、Es、Ek以及ηk的值与偏应力水平Δσ存在一定的函数关系。具体为:固结参数α与偏应力水平Δσ呈线性关系,而蠕变迟滞时间t0、固结参数β、初始模量E0、压缩模量Es、弹性模量Ek以及黏滞系数ηk与偏应力水平Δσ呈指数函数的关系。
将7个模型参数与偏应力水平Δσ的变化关系绘于图 8中,同时进行回归分析,进而得到7个模型参数与偏应力水平Δσ的回归公式(式(11))。
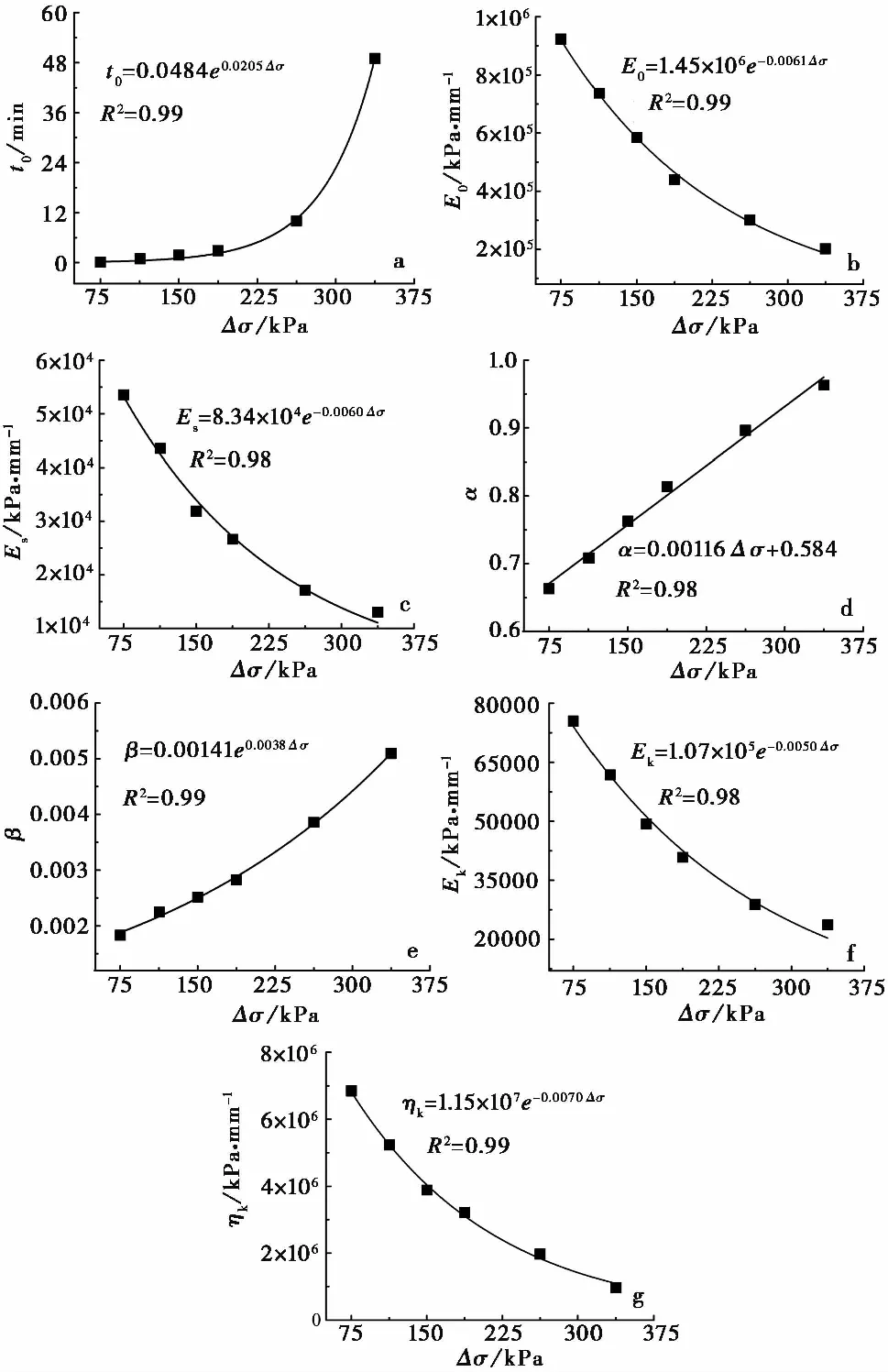
图 8 本文模型参数与偏应力关系曲线Fig. 8 Correlation between model parameters and deviatoric stressa. t0参数拟合; b. E0参数拟合; c. Es参数拟合; d. α参数拟合; e. β参数拟合; f. Ek参数拟合; g. ηk参数拟合
(11)
将式(11)代入式(10)即可建立起考虑固结-蠕变耦合作用的红黏土元件蠕变模型。
3 预测效果分析
利用本文模型对偏应力水平为Δσ5和Δσ7的蠕变曲线(未参与拟合回归分析)进行预测,其结果如图 9。
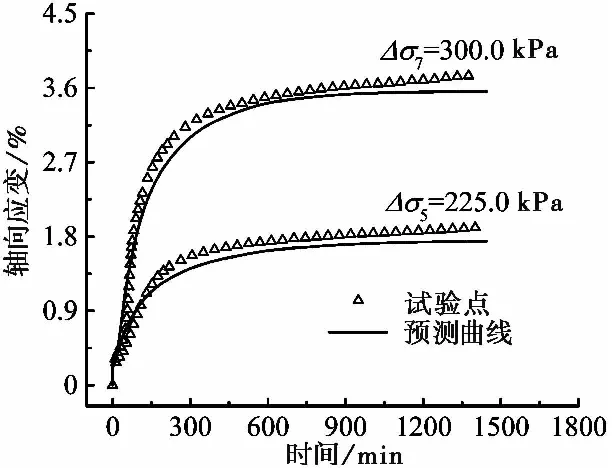
图 9 基于本文模型的蠕变预测Fig. 9 Predicted creep response by using the presented model
预测结果(图 9)表明:本文所提出的针对衰减蠕变曲线且考虑固结-蠕变耦合作用的红黏土元件蠕变模型对红黏土蠕变曲线的预测效果良好。高偏应力水平下的蠕变曲线,其前面部分会存在两个较为明显的拐点,本文模型也基本能够将这两个拐点的位置预测出来。
4 结 论
(1)为深入研究红黏土的蠕变特性,本文在原有的TSZ全自动应变控制式三轴仪的基础上,设计改制了一套基于杠杆加载原理的红黏土三轴蠕变试验装置,并对围压为200ikPa的红黏土试样采用分级加载进行排水三轴蠕变试验,得到了不同应力水平下的蠕变全过程曲线及其蠕变破坏阈值。
(2)通过引入弹簧元件模拟瞬时变形、平均固结度统一表达式模拟固结变形、Kelvin体模拟蠕变变形,同时引入蠕变迟滞时间参数,建立了考虑固结-蠕变耦合作用的红黏土元件蠕变模型。结果表明该模型能够较好地拟合及预测红黏土的蠕变曲线。
(3)红黏土的长期强度和蠕变特性还与固结压力及含水率等因素有关,固结压力及含水率这两个因素对红黏土长期强度和蠕变特性的影响规律将在后期展开进一步的研究。
