First-principles investigation of the concentration effect on equilibrium fractionation of Ca isotopes in forsterite

Yahui Song · Yonghui Li · Wenzhong Wang · Zhongqing Wu

Abstract Previous theoretical studies have found that the concentration variations within a certain range have a prominent effect on inter-mineral equilibrium isotope fractionation (103lnα). Based on the density functional theory,we investigated how the average Ca–O bond length and the reduced partition function ratios (103lnβ) and 103lnα of 44Ca/40Ca in forsterite(Fo)are affected by its Ca concentration. Our results show that Ca–O bond length in forsterite ranges from 2.327 to 2.267 A˚ with the Ca/(Ca + Mg) varying between a narrow range limited by an upper limit of 1/8 and a lower limit of 1/64. However,outside this narrow range,i.e.,Ca/(Ca + Mg)is lower than 1/64 or higher than 1/8, Ca–O bond length becomes insensitive to Ca concentration and maintains to be a constant. Because the 103lnβ is negatively correlated with Ca–O bond length, the 103lnβ significantly increases with decreasing Ca/(Ca + Mg) when 1/64 ＜Ca/(Ca + Mg)＜2/16.As a consequence,the 103lnα between forsterite and other minerals also strongly depend on the Ca content in forsterite.Combining previous studies with our results,the heavier Ca isotopes enrichment sequence in minerals is:forsterite ＞orthopyroxene ＞clinopyroxene ＞calcite ≈diopside ＞dolomite ＞aragonite. Olivine and pyroxenes are enriched in heavier Ca isotope compared to carbonates. The 103lnα between forsterite with a Ca/(Ca + Mg) of 1/64 and clinopyroxene (Ca/Mg = 1/1, i.e.,diopside)is up to ～0.64‰at 1200 K.The large 103lnαFo-diopside relative to the current analytical precision for Ca isotope measurements suggests that the dependence of 103lnαFo-diopside on temperature can be used as a thermometer, similar to the one based on the 103lnα of 44Ca/40Ca between orthopyroxene and diopside.These two Ca isotope thermometers both have a precision approximate to that of elemental thermometers and provide independent constraints on temperature.

Keywords Ca isotope · First-principles calculations ·Forsterite · Concentration effect · Equilibrium isotope fractionation

1 Introduction

Calcium (Ca)ranks fifth among the Earth’s most abundant element and contains six stable isotopes(40Ca,42Ca,43Ca,44Ca,46Ca, and48Ca). It has the largest relative mass difference between48Ca and40Ca up to 20%except after H and He.Ca isotopes have been widely used in exploring Ca recycling in early planetary formation and accretion, the origin of the Earth and Moon (Huang et al. 2012; Kang et al. 2017; Simon and DePaolo 2010; Valdes et al. 2014),mantle and crustal materials recycling (DePaolo 2004;Huang et al. 2011) and the deep carbon cycle (Christina and DePaolo 2000; Fantle and DePaolo 2005; Fantle and Tipper 2014;Farkasˇet al.2016;Heuser et al.2005;Steuber and Buhl 2006).

The Ca stable isotopic composition is usually reported as: δ44/40Ca = [(44Ca/40Ca)Sample/(44Ca/40Ca)SRM-915b- 1] ×1000‰ (Amsellem et al. 2017; Valdes et al. 2014). Large variations in Ca isotope composition were reported even in igneous rocks and their diagenetic minerals. For example,DePaolo (2004) reported that the variation in δ44/40Ca of oceanic basalts is up to ～0.7‰. Amini et al. (2010)reported a δ44/40Ca variation of ～0.9‰ in ultramafic rocks. Huang et al. (2010) revealed that the44Ca/40Ca offsets between co-existing orthopyroxenes (opx) and clinopyroxenes (cpx) in mantle peridotites range from 0.36‰ to 0.75‰. Zhang et al. (2018) reported a large δ44/40Ca variation of ～1‰in mantle olivine.The Ca isotope variations in natural samples play an important role in understanding the Ca isotope composition and variations of the Earth.

Investigations of the Ca isotope fractionation among several minerals suggest that concentration variations within a certain range have significant effects on 103lnα,which may be a non-negligible factor for understanding Ca isotope variations in natural samples (Feng et al. 2014;Wang et al.2017a,b).For example,Feng et al.(2014)and Wang et al. (2017b) revealed that the effect of Ca concentration on Ca isotope of orthopyroxene have an upper limit and lower limit. When the Ca concentration of orthopyroxene is within the narrow range defined by the two limits, the 103lnα between orthopyroxene and other minerals dramatically depend on the Ca concentration of orthopyroxene. Outside of the narrow range, 103lnα are insensitive to the Ca concentration of orthopyroxene.Later,Wang et al.(2017a)and Li et al.(2019)found another kind of concentration effect, namely Ca isotopes in carbonate minerals and K isotope in alkali feldspars depend significantly on the Ca concentration or K concentration in a wide range of the concentration. However, more investigations are needed to figure out whether the Ca concentration effect in olivine exists.Ca isotope composition in olivine is also needed for constraining the δ44/40Ca of the upper mantle.

Forsterite (Mg2SiO4) is the Mg-endmember of olivine,the major mineral in the upper mantle of the Earth. Cadoped forsterite can be generated with a small amount of Ca atoms replacing Mg atoms. In this study, we investigated the 103lnβ of forsterite and 103lnα between forsterite and other minerals with the first-principles calculations, a method widely used for many systems (Feng et al. 2014;Huang et al. 2013, 2014; Li et al. 2019; Qin et al. 2016;Wang et al. 2017a, b; Wu et al. 2015). We focused on the effect of Ca concentration in forsterite on Ca isotope.This work and our previous work (Feng et al. 2014; Li et al.2019; Wang et al. 2017a, b) are not only crucial for understanding the Ca isotope in natural samples but also very helpful for interpreting two kinds of concentration effects represented by Ca concentration effect in orthopyroxene and Ca concentration effect in carbonate (Mg1-x-CaxCO3), respectively.

2 Methods

2.1 Equilibrium isotope fractionation factor

Inter-mineral isotope substitution can cause changes in vibrational frequencies and thus the mass-dependent equilibrium isotope fractionation (Bigeleisen and Mayer 1947;Urey 1947).Under the harmonic approximation,a function βAis defined,which is the reduced partition function ratio,representing the isotope composition between mineral A and the ideal gas of element M:

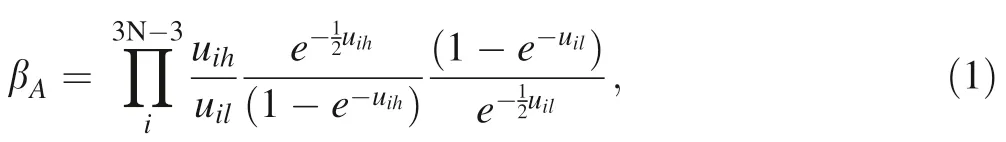
where index h and l represent the heavy and light isotopes,respectively;i and N represent the ith vibrational mode of a unit cell with atoms of N. uiis written as:

where index h represents the Planck constant,ωirepresents the ith vibrational mode, k and T represent the Boltzmann constant and temperature in Kelvin, respectively. Equilibrium isotope fractionation factor of element M between two minerals A and B,αA-B= βA/βB,can be reported by per mil (‰) and written as:

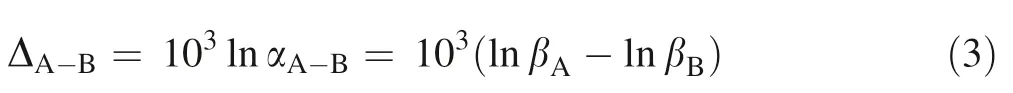
2.2 DFT calculations

Similar to previous work (Feng et al. 2014; Huang et al.2013, 2014, 2019; Li et al. 2019; Qin et al. 2016; Wang et al.2017a,b;Wu et al.2015),the vibrational frequencies of forsterite in this study were calculated by first-principles calculations. The electrical structures were calculated by a software package ‘‘Quantum Espresso’’, which is based upon density functional theory (DFT), plane wave, and pseudopotential (Giannozzi et al. 2009). The approximation type for describing exchange correlation functional was local density approximation (LDA) (Perdew and Zunger 1981), a widely applied approximation in DFT because it works well on predicting crystal structures and calculating vibrational frequencies and isotope fractionation factors(Huang et al. 2013; Wentzcovitch et al. 2010).

The pseudopotential for Ca,Mg,Si,and Mg used in this study is the same as that was used in Wang et al. (2017b).The cutoff threshold for plane-wave energy is set to 70 Ry and the cutoff for residual force was converged below 104Ry/Bohr. The k-point sampling in Brillouin zone was performed on N1× N2× N3mesh (Nirelying on unit cell size, see Table S1). Then, all the crystal structures of Cabearing forsterite with different Ca contents were relaxed following Wentzcovitch (1991)’s method of variable cell shape molecular dynamics. The vibrational frequencies computations were performed on regular q mesh for the unit cell of forsterite and only on gamma-point for supercells of forsterite (see Table S1), following the method of density-functional perturbation theory (DFPT) (Baroni et al. 2001). The vibrational frequency of the 224-atom supercell with a Ca/(Ca + Mg) of 1/64 was computed on Phonopy, a software package following the method of Togo and Tanaka (2015), which shows advantages in computing large systems. The results from calculations only on gamma-point are reliable as our previous study proved that the isotope fractionation factors are not sensitive to dense q point (Li et al. 2019).

3 Results

3.1 Crystal structures

The primitive cell of forsterite has 28 atoms and two nonequivalent sites for Mg atoms (M1and M2). Natural forsterite can contain Ca only in minor or even trace amount.In this study,we replaced Mg with a small amount of Ca to generate Ca-doped structures. Our results found that the total energy of forsterite with Ca replacing Mg atoms in the M1site is larger than that in the M2site, for instance, the energy difference between forsterite [Ca/(Ca + Mg) = 2/16] with Ca in M1site and Ca in M2site is up to ～1.50 eV,which indicates that Ca prefers to replace M2-site Mg atoms in forsterite.

The initial Ca-doped structures of forsterite with variable Ca contents were generated by replacing Mg atoms with the equivalent Ca atoms in the supercells,which were generated by extending the primitive cell of forsterite. For example, forsterite with a Ca/(Ca + Mg) of 1/64 (CaO content of 1.25 wt%) was generated by extending the primitive cell twice along a, b, and c directions and then replacing an M2-site Mg with a Ca in the 224-atom supercell. Similarly, we substituted Mg atoms with the equivalent Ca atoms in the 112-atom,56-atom and 28-atom cells to obtain Ca-doped cells with Ca/(Ca + Mg)of 1/32,2/32, 2/16, and 2/8, corresponding to CaO content of 2.48,4.93, 9.72, and 18.92 wt%, respectively. There are some non-equivalent configurations when using two Ca atoms to replace two Mg atoms. The non-equivalent configurations have slightly different total energy, suggesting the effects of supercell size and orientation anisotropy of extending cell could exist.All the non-equivalent configurations were relaxed and only the configurations with the lowest total energy were conducted vibrational frequencies and 103lnβ calculations. For instance, for forsterite with CaO content of 4.93 wt% (x = 2/32 or 1/16), the total energy sequence of the non-equivalent structures is: Fo2/32bc＜Fo2/32ab＜Fo1/16b＜Fo2/32ac≈Fo1/16c＜Fo1/16a. Here, Fo2/32bcwas selected as the representative of forsterite with the CaO content of 4.93 wt%to conduct vibrational frequency and 103lnβ calculations. We took into account the contributions of the other high-energy configurations to 103lnβ and 103lnα based on their Boltzmann distribution, i.e.,shown in Figs. 4 and 7. The above rules also apply to structures with other CaO contents.

The relaxed forsterite structures with different Ca contents are presented in Fig. 1, highlighting the Ca–O and Mg–O polyhedrons and the optimized cell parameters and volumes in comparison with the experimental results are listed in Table 1. The calculated volumes were smaller than experimental data due to not considering zero-point energy and temperature. However, LDA can achieve good precision for the calculated isotope fractionation results,which is supported by previous studies (Feng et al. 2014;Huang et al. 2019; Li et al. 2019; Me´heut and Schauble 2014; Qin et al. 2016; Wang et al. 2017a, b; Wu et al.2015).

As shown in Fig. 2, the calculated vibrational frequencies agree well with the experimental Raman and Infrared Radiation (IR) frequencies, with the slope between them being 1.004 ± 0.015 (1σ, R2= 0.99978). Take the uncertainty analyses of Me´heut et al.(2009)for reference,an x%relative uncertainty on the calculated frequencies will lead to an x% uncertainty at low temperatures and 2x% at high temperatures on the 103lnβ. The uncertainty of our calculated frequencies is 1.5%, thus under the high temperature interval discussed in this study, e.g., 800–2000 K, the uncertainty of our calculated 103lnβ of forsterite is 3%.According to Feng et al. (2014), the uncertainty of the calculated 103lnβ of diopside is 5%.Since the 103lnα is the difference between the two 103lnβ, the uncertainty of our calculated 103lnαFo-diopsideis 6%.

3.2 CaO bond lengths in forsterite

Average Ca–O bond lengths in forsterite versus different Ca/(Ca + Mg) at static conditions are drawn in Fig. 3 and listed in Table 2. Our calculations show that all the forsterite structures, regardless of their Ca contents have a coordination number(CN)of six,which is equal to the CN of Mg. As discussed in Sect. 3.1, because of the effects of supercell size and orientation anisotropy of extending cell,the structures with the same Ca contents have different total energy and Ca–O bond lengths. Only Ca–O bond lengths of the most stable structures,i.e.,the configurations with the smallest total energy, were shown in Fig. 3 and selected as the representatives to calculate vibrational frequencies and 103lnβ. As shown in Fig. 3, the effect of Ca/(Ca + Mg) on Ca–O bond length is significant in a relatively narrow range of Ca content from 1/8 to 1/64.Within the range, the average Ca–O bond lengths decrease 2.6%from 2.327 A˚ at 1/8 to 2.267 A˚ at 1/64. Outside of the range, the average Ca–O bond length becomes insensitive to the Ca/(Ca + Mg). It only decreases 0.001 A˚from 1/64 to 1/96 and only increases ～0.3% from 2.327 A˚to 2.333 A˚ from 1/8 to 2/8. Thus, similar to the case in orthopyroxene, Ca content effect in forsterite also has an upper limit (1/8) and a lower limit (1/64).

Fig. 1 Relaxed structures of forsterite with different Ca/(Ca + Mg)a 0/8(Pure),b 1/8,c 2/8,d 1/16,e 2/16,f 2/32,g 1/32,h 1/64,i 1/96.Ca cations are cyan;Mg,brown;Si,blue;O,red.The initial structure of forsterite is from American Mineralogist Crystal Structure Database(http://rruff.geo.arizona.edu/AMS/amcsd.php). All the crystal structures are drawn using the software ‘VESTA’’ (Momma and Izumi 2008)

3.3 Ca isotope fractionation

The 103lnβ of44Ca/40Ca of forsterite with different Ca contents are drawn in Fig. 4.The polynomial fitting factors with the temperature ranging from 673 K to 2000 K are reported in Table 3. The equilibrium isotope fractionation factors, 103lnαmineral-diopsideof44Ca/40Ca are drawn in Fig. 5. Their polynomial fitting factors are reported in Table 4. As expected from the effect of Ca/(Ca + Mg) on Ca–O bond lengths, 103lnβ of44Ca/40Ca of forsterite also vary with Ca/(Ca + Mg). For instance, the 103lnβ of forsterite with a Ca/(Ca + Mg) of 1/64 is larger by 0.17‰than the one with a Ca/(Ca + Mg) of 1/32 at 1000 K.Similarly, the 103lnα of44Ca/40Ca between forsterite and minerals are also affected by the Ca content in forsterite.For instance, when the Ca/(Ca + Mg) of forsterite decreases from 2/16 to 1/64, the 103lnα of44Ca/40Ca between forsterite and diopside increase from 0.43‰ to 0.92‰ at 1000 K. Combining previous studies with our results, the enrichment sequence of heavier Ca isotope inminerals is: forsterite ＞orthopyroxene ＞clinopyroxene ＞calcite ≈diopside ＞dolomite ＞aragonite. Furthermore,similar to our previous works,the 103lnαFo-mineralof44Ca/40Ca show negatively linear correlation with the average Ca–O bond length in forsterite (Fig. 6).

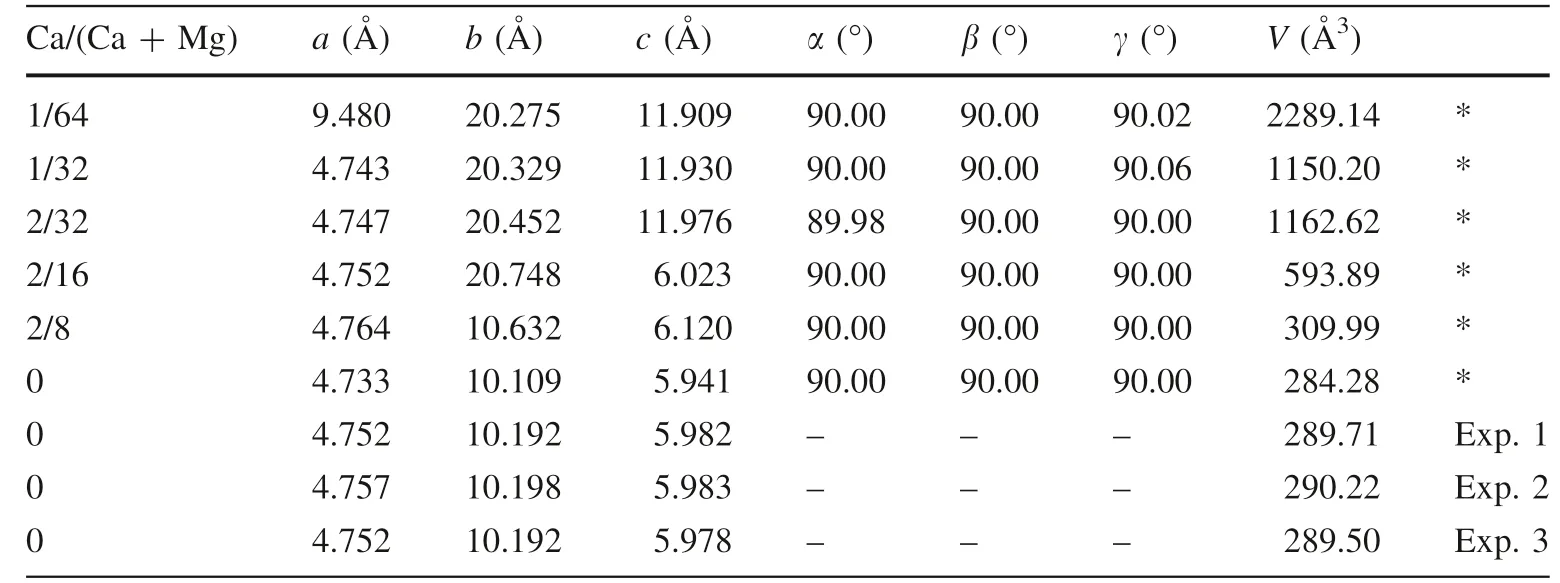
Table 1 The relaxed cell parameters and volumes of forsterite with different Ca/(Ca + Mg) at static conditions and experimental data

Fig. 2 Calculated frequencies of pure forsterite compared with the measured frequencies. Raman data: Chopelas (1990, 1991). IR data:Hofmeister (1987), Sogawa et al. (2006)

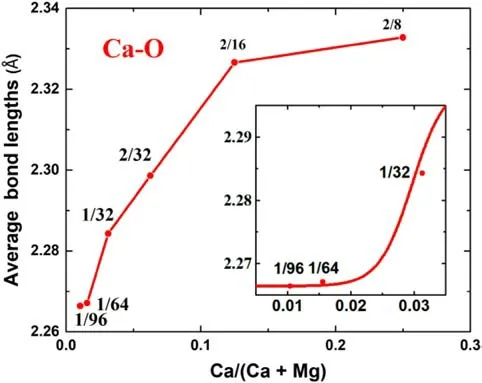
Fig. 3 The average Ca–O bond length versus the Ca/(Ca + Mg) of forsterite

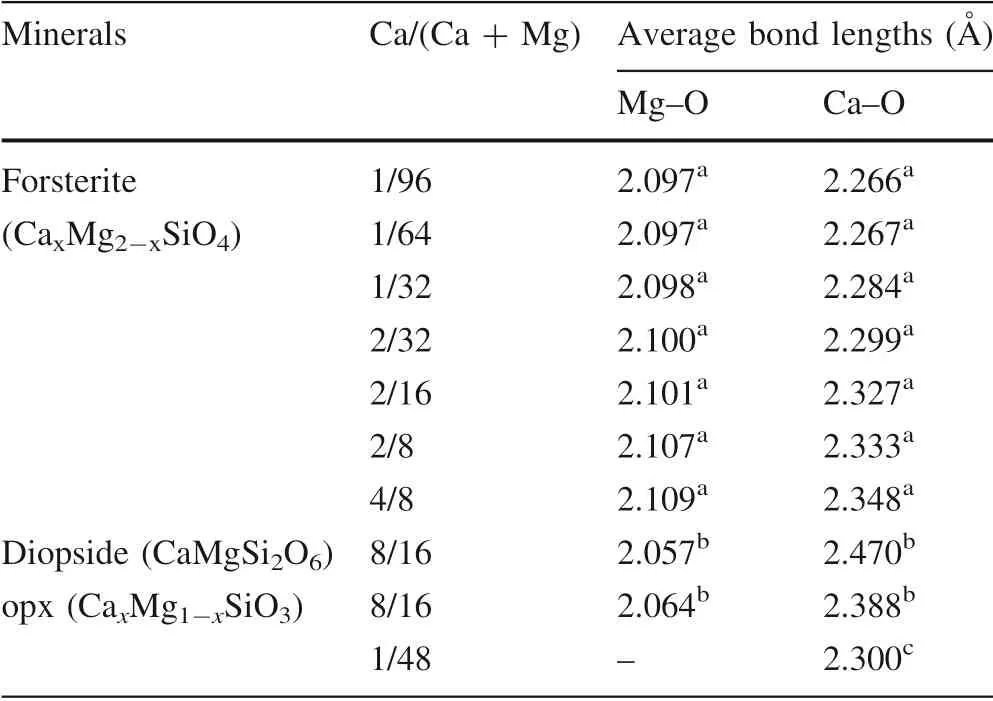
Table 2 Average Mg–O and Ca–O bond lengths at static conditions

Fig. 4 The calculated reduced partition function ratios (103lnβ) of Ca-doped forsterite with variable Ca contents. The 2/8 Bolzm, 2/16 Bolzm and 2/32 Bolzm refer to the estimated 103lnβ taking into account the Boltzmann distribution contributions from the other highenergy configurations

4 Discussion

4.1 Two kinds of concentration effect in minerals

Recently, the work of Feng et al. (2014) and Wang et al.(2017a,b)revealed that Ca–O bond lengths are affected by Ca/Mg ratios in opx and carbonates (e.g. calcite, dolomite and magnesite) and the effects result from the large difference between their Ca2+and Mg2+radius. Li et al.(2019) demonstrated that average K–O bond lengths are affected by the K content in alkali feldspars. Combining their results with ours,we found two kinds of concentration effect on bond lengths. One is represented by Ca concentration effect in orthopyroxene or forsterite. The effect of Ca concentration on the bond lengths in forsterite is similar to that in orthopyroxene. Both have an upper limit and a lower limit.Two limits in each case define a narrow range of Ca content, 1/64 ＜x ＜1/8 for forsterite and 1/48 ＜x ＜1/8 for orthopyroxene (Wang et al. 2017b),within which the Ca–O bond lengths vary significantly with the Ca content. Outside of the range, Ca–O bond lengths are almost independent of the Ca content. The other is represented by Ca concentration effect in carbonate or K concentration in alkali feldspars(Li et al.2019;Wang et al.2017a),where the bond lengths depend significantly on the Ca or K concentration in the wide range of concentration.Ca in natural orthopyroxene and forsterite is a minor or trace element. Instead, Ca in carbonate or K in alkali feldspar could be a major element since calcite and magnesite, as well as albite and microcline, can form a solid solution over a wide range of composition. This is a fundamental difference between systems with different kinds of concentration effect. However, no matter what kind of concentration effect, there should be a lower limit in concentration below which the bond length does not change with the concentration. This is because the local environment of the element does not vary with concentration atextremely low concentration. Intra-Ca-cation distance for forsterite at its lower limit x = 1/64(13.884 A˚)is similar to that for orthopyroxene at its lower limit x = 1/48(14.111 A˚). Other minerals at their lower limit of Ca content should have similar intra-Ca-cation distance. This provides a way to estimate the lower limit for other minerals.

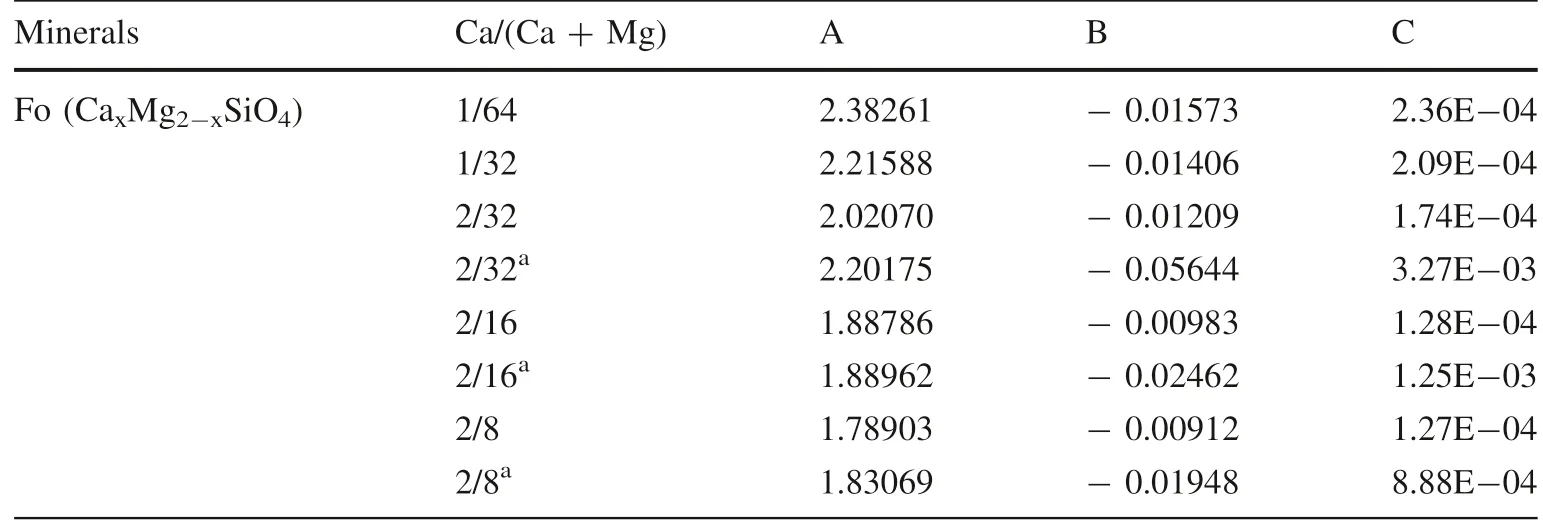
Table 3 Polynomial fitting factors of the reduced partition function ratios (103lnβ of 44Ca/40Ca) for forsterite with different Ca contents

Fig. 5 The equilibrium isotope fractionation factors of 44Ca/40Ca of(a)103lnαFo-diopside(b)103lnαmineral-diopside.Ratios in the figures refer to the Ca/(Ca + Mg) of the minerals

Table 4 Polynomial fitting factors of equilibrium isotope fractionation factors (103lnα) of 44Ca/40Ca between minerals(including forsterite, opx and cpx with different Ca contents,diopside, calcite, dolomite and aragonite) and diopside

Fig. 6 The negative correlation between 103lnαFo-mineral and the average Ca–O bond length in forsterite at 1000 K. Ratios in the figure refer to the Ca/(Ca + Mg) of the minerals

4.2 Concentration effect on isotope fractionation factors

Combining previous work (Feng et al. 2014; Wang et al.2017a, b) with ours, we found that 103lnαmineral-diopsideof44Ca/40Ca show similar negative linear correlation with Ca–O bond length in forsterite (Fig. 6), in consistent with the Ca isotope behavior in pyroxene and carbonate and the K isotope behavior in alkali feldspars (Li et al. 2019). The correlation resulting from the concentration effect is much better than the correlation between 103lnβ of minerals and their corresponding bond length (Qin et al. 2016). As discussed in previous studies (Bigeleisen and Mayer 1947;Urey 1947), 103lnα are controlled by relevant bond strengths. To be specific, longer Ca–O bond usually leads to smaller Ca–O bond strength and lower vibrational frequency, which will result in the enrichment of lighter Ca isotope compared to shorter Ca–O bond (Feng et al. 2014;Hill and Schauble 2008; Li et al. 2019; Qin et al. 2016;Schauble et al. 2004; Urey 1947; Wang et al. 2017a, b;Young et al. 2009). Since other factors such as CN and second nearest-neighbor atoms can also affect the bond strength, the equilibrium isotope fractionation factors are usually not well correlated with the bond length(Qin et al.2016). However, in this and previous cases (Feng et al.2014; Huang et al. 2019; Li et al. 2019; Wang et al.2017a, b), the concentration variation does not change the CN and second nearest-neighbor atoms.The bond strength can be well represented by the bond length,which produces a good linear correlation between the isotope fractionation factors and bond length (see Fig. 6). Although the 103lnβ of44Ca/40Ca of forsterite with x = 1/96 with a 336-atom cell was not calculated because of the limitation of the computation capabilities, we can predict that the 103lnβ and 103lnαFo-diopsideof44Ca/40Ca of forsterite with x = 1/96 are pretty close to those of forsterite with x = 1/64 (see inset of Fig. 7)because they have nearly equal Ca–O bond lengths (see inset of Fig. 3). Therefore, the calculated 103lnβ of forsterite with x = 1/64 should be the representative for calculating equilibrium Ca isotope fractionation factors between forsterite and other minerals since the Ca content (Ca/(Ca + Mg)) in natural forsterite is mostly not more than 1/64 (Libourel 1999; Mohanan et al. 1993;Simkin and Smith 1970;Stormer Jr 1972;Warner and Luth 1973).

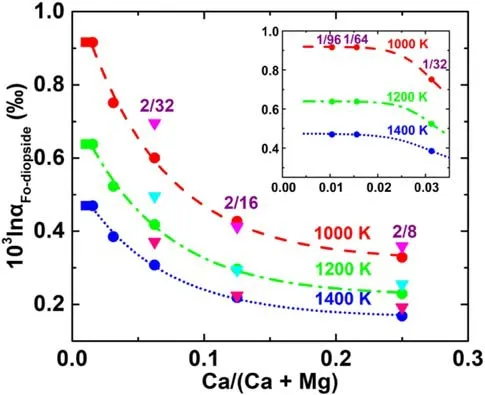
Fig. 7 The dependence of 103lnαFo-diopside of 44Ca/40Ca on Ca/(Ca + Mg) at different temperatures. The dash, dash-dot and shortdot lines represent nonlinear fitting curves of the ‘‘most stable’ data with R2 of 0.99. The magenta, cyan and pink inverted triangles represent the estimated 103lnα considering the contributions from the other high-energy configurations

Since Ca–O bond length of forsterite depends on Ca content only in a limited range of Ca content, the Ca concentration effect on Ca isotope is significant only between an upper limit and a lower limit, The Ca content range is 1/64 ＜x ＜1/8 for forsterite and 1/48 ＜x ＜1/8 for orthopyroxene (Wang et al. 2017b). We can expect a similarly narrow range of Ca content for the minerals where Ca is a minor or trace element. The Ca contents of some natural minerals vary within the narrow range.Thus,the Ca content in natural minerals is a non-negligible factor that controls the equilibrium Ca isotope fractionations between minerals.

The contributions from the other high-energy configurations to the 103lnβ and 103lnα were estimated by the energies and structures of the configurations based on the Boltzmann distribution and the linear relationship between 103lnαFo-diopsideof44Ca/40Ca and the average Ca–O bond length in forsterite. The contributions from the other highenergy configurations to 103lnα are drawn in Fig. 7. For instance,the 103lnα of44Ca/40Ca between forsterite with a Ca/(Ca + Mg) of 2/32 and diopside changes by 0.08‰ at 1200 K.

Fig. 8 Correlation between temperature and 103lnαFo-diopside potentially used as a Ca isotope thermometer. SEE is standard error estimation. The red curve on the left plot represents forsterite with x = 1/64 and the red and blue dash dot curve on the right plot represent the 1σ and 2σ SEE, respectively

4.3 Forsterite-diopside Ca isotope thermometer

103lnαFo1/64-diopsideof44Ca/40Ca is 0.23‰even at 2000 K,the relationship between 103lnαFo-diopsideand temperature could be used as a potential thermometer (Fig. 8). For instance, the estimated 103lnα of44Ca/40Ca between forsterite and diopside range from 0.64‰ to 0.92‰ when the temperature decreases from 1200 K to 1000 K. The Standard error of the estimation (SEE) of temperature was obtained using the current analytical precision (0.05‰,2se) (Huang and Jacobsen 2017; Kang et al. 2016; Lehn et al.2013;Zhao et al.2017)and the uncertainty of 103lnα of44Ca/40Ca between forsterite and diopside.For example,the estimated 1σ SEE at 1200 K is ～59 K using our forsterite-diopside thermometer, with a precision approximate to orthopyroxene-diopside Ca isotope thermometer(Wang et al. 2017b) and elemental thermometers (Putirka 2008, 2016).

5 Conclusions

The effect of Ca concentration in forsterite on its average Ca–O bond length and 103lnαFo-mineralof44Ca/40Ca was investigated in detail in this study. Our calculations show the average Ca–O bond length increases by 2.6% from 2.267 A˚ to 2.327 A˚ when Ca/(Ca + Mg) increases from 1/64 to 2/16 and almost remains a constant when x drops from 1/64 to 1/96. The reduced partition function ratios,103lnβ also vary with the Ca/(Ca + Mg) within the Ca concentration range of 1/64 to 1/8.Combining previous studies with ours, we found two kinds of concentration effect.One is represented by forsterite or orthopyroxene in which the concentration effect is significant only in a limited Ca content range bounded by an upper limit and a lower limit. The other is represented by carbonates or feldspars in which the concentration effect range is significant in a wide range of Ca or K content range.

The calculated 103lnα between Ca-bearing minerals reveal that olivine is more enriched in heavier Ca isotope than pyroxenes and carbonates.The enrichment sequence of heavier Ca isotope in minerals is: forsterite ＞orthopyroxene ＞clinopyroxene ＞calcite ≈diopside ＞dolomite ＞aragonite. Similar to the orthopyroxene-diopside thermometer,the dependence of 103lnαFo-diopsideon temperature can be a potential olivine-pyroxene thermometer with precision approximate to that of elemental thermometers.Finally,the concentration effect on isotope fractionations are likely to be widespread in naturally occurring minerals and the concentration effect should not be neglected in future isotope studies.

AcknowledgementsThis work is financially supported by the Natural Science Foundation of China (Nos. 41721002, 41473011), and Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund. The computations were conducted partly in the Supercomputing Center of the University of Science and Technology of China.

Compliance with ethical standards

Conflict of interestOn behalf of all authors, the corresponding author states that there is no conflict of interest.