Equilibrium thallium isotope fractionation and its constraint on Earth's late veneer

Tong Fang· Yun Liu

Abstract Equilibrium isotope fractionation of thallium(Tl) includes the traditional mass-dependent isotope fractionation effect and the nuclear volume effect (NVE). The NVE dominates the overall isotope fractionation, especially at high temperatures. Heavy Tl isotopes tend to be enriched in oxidized Tl3+-bearing species. Our NVE fractionation results of oxidizing Tl+ to Tl3+ can explain the positive enrichments observed in ferromanganese sediments. Experimental results indicate that there could be 0.2–0.3 ε-unit fractionation between sulfides and silicates at 1650 °C. It is consistent with our calculation results,which are in the range of 0.17–0.38 ε-unit. Importantly,Tl’s concentration in the bulk silicate Earth (BSE) can be used to constrain the amount of materials delivered to Earth during the late veneer accretion stage. Because the Tl concentration in BSE is very low and its Tl isotope composition is similar with that of chondrites,suggesting either no Tl isotope fractionation occurred during numerous evaporation events, or the Tl in current BSE was totally delivered by late veneer. If it is the latter, the Tl-contentbased estimation could challenge the magnitude of late veneer which had been constrained by the amount of highly siderophile elements in BSE.Our results show that the lateaccreted mass is at least five-times larger than the previously suggested magnitude,i.e.,0.5 wt%of current Earth’s mass. The slightly lighter 205Tl composition of BSE relative to chondrites is probable a sign of occurrence of Tlbearing sulfides, which probably were removed from the mantle in the last accretion stage of the Earth.

Keywords Equilibrium Tl isotope fractionation · Nuclear volume effect · Tl fractionations between silicates and sulfides · Late veneer · First-principles calculation✉

1 Introduction

The thallium (Tl) isotope system has been used as a highprecision tool to trace geologic processes since the techniques used to measure Tl isotope ratio became enhanced in 1999 (Rehkamper and Halliday 1999). Tl is a lithophile and chalcophile element (Shaw 1952; McGoldrick et al.1979; Wood et al. 2008), and as such it is present in both silicate and sulfide phases. The knowledge of elemental partition and isotope fractionation for Tl is vitally essential for Tl to be used as tracers in the study of the Earth’s differentiation processes.Tl is likely to enter the metal core if a sulfide phase exists, causing Tl to undergo elemental partition and isotope fractionations during core-mantle differentiation (Wood et al. 2008). Hence, the Tl isotope fractionation factors of the coexisting phases between silicates and sulfides are very important to deciphering the magmatic evolution in the accretion stage of Earth.

Tl behaves as an incompatible element during the process of magmatic crystallization and differentiation (Shaw 1952). Tl+ion can be replaced by the ions of alkali metal,such as K+and Rb+,in phyllosilicate and feldspar minerals(Shaw 1952; Heinrichs et al. 1980). Thallium is a highly volatile element; its equilibrium condensation temperature is 532 K in the form of troilite (Tl2S, Tl2Se, Tl2Te)(Lodders 2003). During the processes of evaporation and condensation in the accretion of Earth, the loss or migration of Tl could result in stable Tl isotope fractionation in addition to possible dynamic fractionation.We can use the first-principles calculation to estimate such equilibrium Tl isotope fractionations.

Thallium has two isotopes in nature, i.e.,203Tl (29.5%)and205Tl (70.5%). The isotope fractionation factor of Tl isotopes, ε205Tl, denotes the deviation of205Tl/203Tl in parts per 10,000 relative to the standard sample (NIST SRM 997 Tl metal). The variation of ε205Tl for terrestrial samples is more than 35 ε205Tl. The largest fractionation was observed between the low temperature altered oceanic crust (- 20 ε205Tl) and Fe–Mn sediments (+ 15 ε205Tl)(Rehkamper et al.2002;Nielsen et al.2006b,2013,2015).Various meteorites have been shown to exhibit a wide range, with variations even as high as 50 ε205Tl (Nielsen et al. 2006a; Andreasen et al. 2009; Palk et al. 2011;Nielsen et al. 2017). The ε205Tl of an outlier for carbonaceous chondrites is about 5.2, ranged from - 4 to 1.2,which is proportional to the ratio of Pb/Tl (Baker et al.2010). This relationship results from the decay of205Pb to205Tl and the differentiation of Pb/Tl in the early solar system (Baker et al. 2010). The composition of ε205Tl for ordinary chondrites ranges from - 20 to + 15, and this large fractionation is probably caused by the thermal metamorphism (Andreasen et al. 2009). Enstatite chondrites exhibits ε205Tl values ranging from - 2.9 to + 0.8(Palk et al. 2011). For iron meteorites, ε205Tl exhibits an extremely large variation spanning about 50 ε (- 19 to+ 30) (Nielsen et al. 2006a; Andreasen et al. 2009). The maximal variation of ε205Tl is believed to be produced by the decay of205Pb under different environments with different Pb/Tl ratio. Another explanation is the kinetic isotope effect of stable isotope fractionation on205Tl/203Tl during the process of evaporation and condensation(Nielsen et al. 2006a). The205Pb-205Tl system can be a promising tool for dating the early solar system events with a short half-life of 15.1 Ma (Pengra et al. 1978). It is believed that the extinct nuclide205Pb was formed by the nucleosynthesis s-process (Yokoi et al. 1985). The initial composition of205Pb of the solar system was determined by isochronal dating method using a group of carbonaceous chondrites (Baker et al. 2010).

The average ε205Tl in the bulk silicate Earth (BSE) is around - 2, similar to that in continental crust and Midocean ridge basalt (MORB) (Nielsen et al.2005,2006b,2007). The variation in ε205Tl among natural terrestrial samples is measurable, and the fractionations were proved to be considerable, ranging from - 20 to+ 15 ε205Tl(Rader et al.2018).Moreover,sulfide minerals contain the heaviest Tl isotope signals, and Fe-rich micas show the minor value of ε205Tl(Rader et al.2018).In highpressure and high-temperature experiments, the Tl isotope fractionation between the silicate and sulfide reached to 0.2–0.3 ε205Tl and the fractionation between the silicate and the metal reached 1.1 ε205Tl at about 1650 °C (Wood et al.2008).The reason for Tl isotope fractionations at such high temperatures has not been carefully investigated yet.

The relative mass difference of thallium’s two isotopes is tiny. Therefore, it is likely that the mass-dependence fractionation contribution is a secondary factor for the overall equilibrium Tl isotope fractionation (Bigeleisen 1996; Fujii et al.2013; Moynier et al.2013).Tl is a heavy metal element with an atomic number of 81. Thallium exists mostly as Tl(I) in nature, but under an extremely oxidized condition or in surface environments Tl can exist as Tl()(Nielsen et al.2017;Rader et al.2018).There is a difference of two s electrons between two oxidation states.Therefore, considerable contributions of Tl isotope fractionation could be brought by the nuclear volume effect(NVE) (Schauble 2007; Nielsen 2011; Fujii et al. 2013;Moynier et al. 2013; Hettmann et al. 2014; Yang and Liu 2015). The directions of both mass-dependent and NVEdriven stable isotope fractionations are the same. The oxidized species (Tl()) are enriched in heavier Tl isotopes (Schauble 2007; Yang and Liu 2015). It has been proved that the traditional mass-dependent takes up about 25% of the total equilibrium fractionation at room temperature (Fujii et al. 2013).

The NVE is also known as the nuclear field shift(NFS).It is produced by the deviation of the nuclear field with different nuclear size for isotopes, which leads to the different electronic energy and density at the nuclei (Bigeleisen 1996; Schauble 2007). The NVE becomes larger as atomic mass increases. Heavy isotopes prefer to go into species with smaller electronic densities at the nucleus(Schauble 2007). Although previous studies have devoted to calculating the NVE-driven fractionations of Tl-bearing small species (Schauble 2007; Fujii et al. 2013; Yang and Liu 2015), none of these studies have calculated the NVEdriven fractionations for Tl-bearing crystalline materials(e.g., minerals). In this study, we calculated Tl isotope equilibrium fractionation factors for Tl-bearing ions,molecules, radicals and minerals under different temperatures. Our aim is to provide a foundation of equilibrium isotope fractionation studies of Tl isotope geochemistry and help people to explain observed Tl isotope signals in nature.

2 Methods

Equilibrium isotope fractionation for heavy elements (Pb,U,W,Tl,Os,etc.)contains the effect of mass shifts（ln α0）and the nuclear field shift (i.e., the nuclear volume effect)ln（ ） (Bigeleisen 1996). The mass-dependent fractionation scales with δm/mm, and it declines with the decrease of the relative mass difference between different isotopes.When the atomic number is larger than 40,massdependent fractionation becomes very small even at ambient temperatures. Therefore, the NVE becomes the dominant factor of the total equilibrium isotope fractionation of heavy metal isotope systems(Pb,U,W,Tl,Os,etc.)(Bigeleisen 1996; Schauble 2007).

Based on the classical method suggested by Bigeleisen and Mayer (1947) and Urey (1947), the pure harmonic vibrational frequencies are required for the calculation of mass-dependent fractionation.Here,we follow the methods and procedures used in Schauble(2007)and Yang and Liu(2015) to calculate the mass-dependent part of Tl isotope fractionations. For gaseous molecules and ions containing Tl+and Tl3+, the Hartree–Fock (HF) method was applied in the Gaussian 09 software package (Frisch et al. 2009).The relativistic pseudopotential is used to consider the inner electronic potential energy, and we use the contraction double-zeta basis set cc-pVDZ-PP as the basis set for the outer electrons and the non-pseudopotential doublezeta basis set (cc-pVDZ) is chosen as the basis set for the light element (H, O, F, Cl, Br). Similarly, the results demonstrate that the contribution of mass-dependent fractionation is much smaller than that of NVE (Table 1).

Table 1 Mass dependent fractionations=10，000· of Tl-bearing molecules relative to Tl atom, calculated in this study

Table 1 Mass dependent fractionations=10，000· of Tl-bearing molecules relative to Tl atom, calculated in this study

substance 0 °C 25 °C 100 °C 300 °C 1000 °C 3000 °C Tl 0.00 0.00 0.00 0.00 0.00 0.00 Tl+ 0.00 0.00 0.00 0.00 0.00 0.00 Tl3+ 0.00 0.00 0.00 0.00 0.00 0.00 TlF 2.20 1.88 1.24 0.54 0.11 0.02 TlF3 9.37 8.03 5.34 2.37 0.49 0.08 TlCl 1.14 0.96 0.62 0.27 0.05 0.01 TlCl3 5.93 5.02 3.25 1.40 0.29 0.04 TlBr 1.01 0.85 0.55 0.23 0.05 0.01 TlBr3 5.25 4.43 2.85 1.22 0.25 0.04 Tl2O 4.57 3.89 2.54 1.11 0.23 0.03 Tl2S 2.30 1.94 1.25 0.53 0.11 0.02 Tl(H2O)3+ 0.84 0.71 0.45 0.19 0.04 0.01 Tl(H2O)63+ 6.78 5.75 3.75 1.62 0.33 0.05

The nuclear field effect depends on the electronic density at the nucleus and the charge, shape, and size of the nucleus (Bigeleisen 1996). In this study, we only take into account the finite volume of the nucleus with spherical shapes of an atomic nucleus because the NVE dominates the nuclear field effect (Schauble 2013; Yang and Liu 2015, 2016). There are two quantum-chemistry-based methods that can be used to calculate the NVE-driven isotope fractionation. The first method is based on the change of ground-state electronic energy between two isotopologues.The fractionation factor can be expressed as(Bigeleisen 1996):

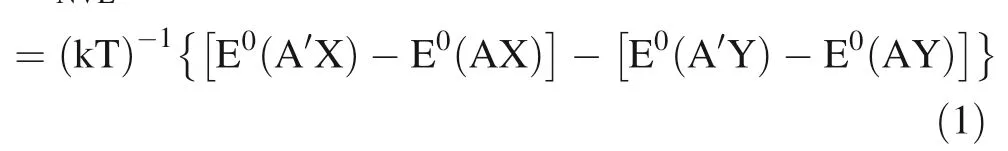
where A and A’ are light and heavy isotope of element A.E0is the minimum of ground state electronic potential energy for two isotopologues AX and AY.

Several previous studies have used the Dirac–Hartree–Fock method to calculate the electronic energy of Tlbearing species(Schauble 2007;Fujii et al.2013;Yang and Liu 2015).Basis sets are set as four-component relativistic Gaussian basis sets for the heavy element. For open-shell systems, the complete open shell configuration (COSCI)method is considered. Three methods are accomplished with Dirac04, GRASP2 K and UTChem program respectively. There are small differences in the results of these methods(Table 2).Unfortunately,this ground-state energy calculation method can only be applied to systems with no more than 20 atoms (Schauble 2013), because the calculation of electronic energy in large systems is too computationally expensive and it is hard to obtain the required accuracy.

Another method, which can be applied into solid and liquid systems, is to obtain the NVE-driven fractionation factor from the electronic density at the nucleus. The difference of electronic energy between light- and heavyisotope containing systems can be written as a relation of effective electronic density and the difference of meansquare nuclear charge radii (Almoukhalalati et al. 2016):

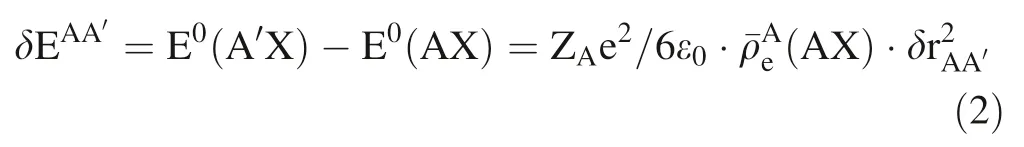
where ZAis atomic number of element A, e is an elementary charge (1.60217733 ×C), ε0is permittivity of free space (8.854187817 ×F/m), δr2AA′is the difference of mean-squared nuclear radii between205Tl and203Tl which can be obtained from (Angeli and Marinova 2013), and ¯ρAeis the effective electronic densities at the nucleus of A in the target substance. Hence, we can deduce another formula from Eqs. (1) and (2) written as lnKfs:

Table 2 The comparison of NVE-driven fractionations (in ε205Tl) of Tl-bearing species relative to Tl atom at 298 K

High-precision NVE calculations for solid systems need precise effective electronic densities based on the second method, but it is hard to achieve. The effective electronic density at the nucleus can typically be approximated by the so-called ‘‘contact electronic density’’, which may lead to ～10% errors (Almoukhalalati et al. 2016). The reason is that the contact density is the electronic density at the origin r = 0 position of atom nucleus (Mastalerz et al.2010), while the effective density represents electronic density at a radius inside the nuclear volume from 0 to R.We can obtain the average density of points on a small sphere around the center of a nucleus in ADF code, which can be a good approximation of the effective electronic energy and is a better treatment compared to that of the contact density.

There is only one previous study of NVE calculation for crystalline systems, and its focus was on Hg, Cd and Sn isotope systems (Schauble 2013). That study used the projector augmented wave (PAW)method implemented in ABINIT code and considered scalar relativistic treatment and Gaussian finite nuclear module to calculate the contact density at the nucleus for crystalline systems.

In this study, instead of calculating the contact density,we directly calculated the effective electronic density at the nucleus for both molecules and crystalline systems by using ADF software and BAND module built in it (Velde and Baerends 1991;Guerra et al.1998;Velde et al.2001).ADF provides the basis sets of Slater-type for all elements.It is well-known that Slater-type basis sets can be more accurate to calculate nuclear cusp and long-range behaviors than Gaussian-type basis sets.

When the properties of heavy elements are calculated,it is reasonable to use the zeroth-order regular approximated(ZORA)relativistic approach and a Gaussian finite nucleus module. For gaseous molecules and ions, we used QZ4P(quadruple zeta with four polarization functions) ZORA basis sets to obtain very accurate results.For solid systems,TZ2P (triple zeta with two polarization functions) was selected, which helps to save calculation time and gets accurate results at the same time. We used the GGA-PBE functional with DFT approach to calculating electronic density at the nucleus in this study. When managing the aqueous species in water, we used the COSMO (Conductor-like Screening Model) solvation model to account for the solvation effects. As a result, the fractionation factors driven-by NVE can be obtained from Eq. (3) using the results of electronic densities at the nucleus. The comparison of the results of fractionation factors calculated in this study and the results from previous studies for Tl-bearing ions, molecules and radicals are shown in Table 2. The reason for the differences of final results is that the type of basis sets we used in this study is Slater-type, while other studies used Gaussian-type orbitals.

3 Results

The ε notation is commonly used for Tl isotope composition for natural samples:

Accordingly, the calculated NVE-driven Tl isotope fractionation is written as

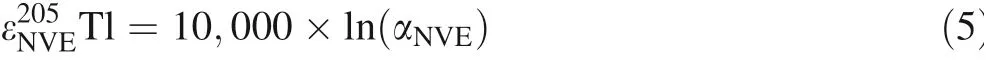
where αNVEis the isotope fractionation factor caused by the NVE. The mass-dependent Tl isotope fractionation is expressed as

where αMDis the isotope fractionation factor caused by mass-dependent isotope effect, which usually is governed by the Bigeleisen-Mayer equation or the Urey model(Bigeleisen and Mayer 1947; Urey 1947).

3.1 Mass-dependent fractionations in Tl-bearing systems

First, we have known that the traditional mass-dependent fractionation is much less than the NVE-driven fractionation for Tl isotope system (Fujii et al. 2013). The massdependent (MD) fractionation factor is proportional to δm/mm’ and 1/T2(ln αMD∝δm/mm’T2) and the NVEdriven fractionation factor is proportional to the difference of mean-square nuclear radii and 1/T (ln αNVE∝δr2/T).The above two relationships indicate that the small relative mass difference between203Tl and205Tl causes a minor mass-dependent fractionation, while the NVE-driven fractionation becomes the dominant factor for the overall fractionation, especially at high temperatures (Schauble 2007) (Tables 1, 3).

3.2 NVE-driven fractionations for Tl-bearing ions,molecules and radicals

The magnitude of the NVE is controlled by the oxidation states, the coordination number of Tl and the electronegativity of adjacent atoms to Tl. Tl mainly maintains two oxidation states (Tl(I) and Tl()). The results of NVEdriven fractionation for Tl-bearing ions, molecules and radicals suggest that heavier isotope205Tl will be enriched in oxidized states (i.e., Tl3+-bearing species) compared to reduced states(Tl+-bearing species)(Table 3).This rule of thumb has been suggested by previous studies (Schauble 2007; Fujii et al. 2013; Yang and Liu 2015). The largest equilibrium Tl isotope fractionation between Tl3+ions and Tl+ions is 21.44(in 10-4)at 25 °C(see Table 3 and there is no classical MD fractionation between Tl3+ions and Tl+ions).

It has been known that a decrease in s-shell electrons,as well as an increase in p, d, f electrons, could lead to less electronic density at the nucleus. Tl-species with less electronic density tend to be enriched in heavier isotopes and consequently exhibit a larger ε205Tl value.Conversely,a heavy element with larger electronic densities at the nucleus can have a deficit of ε205Tl (Bigeleisen 1996;Schauble 2007). The electron configuration of the Tl+ion is ((Xe)4f145d106s2), which has one p-shell electron less than that of Tl atom ((Xe)4f145d106s26p1). Therefore, Tl+ion has larger electronic densities and a negative value of ε205Tl relative to Tl atom.The Tl3+ion((Xe)4f145d10)has two s-shell electrons less than Tl+ion ((Xe)4f145d106s2),hence Tl3+ion has a smaller electronic density than both Tl+ion and Tl atom. Heavier Tl isotopes should be enriched in Tl3+species and to produce a large positive value of ε205Tl (if relative to Tl). When Tl+ion is connected to an anion, such as O2-, F-, Cl-, and Br-, the outer s-shell electrons of Tl+will be shared by that anion. It decreases the electronic density at the nucleus of Tl. Specifically,when bonded to Tl, the electronic density declines as this order: Tl-O＞Tl-F＞Tl-Cl＞Tl-Br. Such bonding produces a higher ε205Tl value than that of Tl (Fig. 1a). On the contrary, the sharing of d electrons in the outer layer will increase the electronic density at the nucleus and decrease the value of ε205Tl for Tl3+–bearing systems. Compared Tl3+ion with Tl(H2O)3+, Tl(H2O)33+and Tl(H2O)63+, we can find that the results of fractionation factors are similar to each other, while the composition of205Tl for Tl3+ion shows a bit heavier than the aqueous phases (Fig. 1b). As for Tl+–bearing species, most of the aqueous phases show larger values of ε205Tl compared to Tl+ion. These characteristics are shown in Table 3.

Tl generally exists as Tl(I) in nature, and Tl(III) only exists in the surface environment or under high oxidizing conditions. Tl exists as Tl+ion or TlCl in seawater. It has been reported that Tl+in the seawater can be oxidized to Tl3+on the surface of manganese-oxide(birnessite)during the process of absorption. This absorption could lead to an enrichment of Tl content and also205Tl (Bidoglio et al.1993; Peacock and Moon 2012). Tl could enter in the vacancy of hexagonal birnessite and be oxidized to Tl3+while Mn4+would be reduced to Mn2+. According to the structure of sorption Tl in hexagonal birnessite observed in the experiments (Peacock and Moon 2012), Tl is tetrahedral with O atoms in the vacancy position. Two kinds of spatial structure of hexagonal birnessite were constructed.They are Tl_HxBir_pH8_2 h (Fig. 2a) and Tl_HxBir_pH8_336 h(Fig. 2b)(Peacock and Moon 2012).They are C3 symmetric, and their bond length is the same as that of Tl2O3.Other types of manganese oxides,such as todorokite, triclinic birnessite, and ferrihydrite, do not show the deficit of ε205Tl and the transformation of the oxidation state for Tl. Therefore, the content of hexagonal birnessite in ferromanganese sediments determined the total redox state of Tl, the content of Tl element and isotope composition of205Tl. It is not confirmed yet whether the apparent enrichment of205Tl in ferromanganese sediments could be explained by the NVE-driven fractionation during exchanging process of Tl species between birnessite and seawater. We use two types of tetrahedral structure of Tl3+in hexagonal birnessite (i.e., Tl_HxBir_pH8_2 h and Tl_HxBir_pH8_336 h) as suggested in a previous study(Peacock and Moon 2012) to represent the Tl-bearing birnessite, and use Tl+or TlCl in solution as the aqueous Tl+phase in seawater. The final fractionation results of such exchange reaction can reach to 9.57 ε-unit at 25 °C(Table 4). This calculation has used the COSMO solvent model method to account for possible solvation effects.

Table 3 Nuclear volume fractionations(3 =10，000·βN20V5-203)of Tl-bearing molecules relative to Tl atom,calculated in this study

Table 3 Nuclear volume fractionations(3 =10，000·βN20V5-203)of Tl-bearing molecules relative to Tl atom,calculated in this study

?

3. 3 NVE-driven Tl isotope fractionations for crystalline compounds

As a lithophile element, Tl+ion can replace K+in micas and feldspar due to their similar ion radius (Rader et al.2018). Tl element also displays chalcophile characteristic and tends to form a covalent bond in sulfides (Wood et al.2008; Kiseeva and Wood 2013). Hence, the Tl+ion can replace Ag+or Pb2+in sulfides and sulfosalts(Rader et al.2018). It has been reported that sulfides contain the larger value of ε205Tl and in contrast,micas and feldspar show the smaller values from the observations of natural samples.In this study, we calculated NVE-driven fractionation factors of many Tl-bearing crystalline compounds and minerals,relative to Tl crystal(Fm3m)(Olsen et al.1994)(Table 4).The structures of crystalline compounds have been shown in Fig. 3. The results of the calculated Tl isotope fractionations are consistent with the results from measurements, which show maximum values of ε205Tl in sulfides and the deficits of205Tl in feldspar, muscovite, phlogopite and orthoclase, etc. The largest fractionation between the coexisting phases with the same oxidation state (Tl+) can reach to 0.95 ε-unit at 300 °C.

4 Discussion

4.1 Possible Tl isotope fractionations during analysis procedures

The measurement method of thallium isotopes has been largely improved since the late 1990s by using multiple collectors inductively coupled plasma-mass (MC-ICPMS)(Rehkamper and Halliday 1999), which provides a high precision of 0.01–0.02% for the ratio of205Tl/203Tl compared with previous studies measured by NTIMS (Nielsen et al.2017).They used the power law with a known ratio of208Pb/206Pb in solution to correct the mass bias of205Tl/203Tl.This approach can help to clear the equilibrium and kinetic fractionations that are mass-dependent during the experiment (Rehkamper and Halliday 1999; Nielsen et al. 2004). However, there must be NVEs during the chemical treatment processes and mass spectrometric analysis.

Fig. 1 a Tl isotope fractionations driven by the nuclear volume effect for Tl+-bearing ions and molecules relative to Tl atom; b Tl isotope fractionations driven by the nuclear volume effect for Tl3+-bearing ions and molecules relative to Tl atom

Thallium mostly exists as Tl+ion with a small amount of Tl3+ion(0.2–0.5%)coexisting in measured solutions at ambient temperature environment (Fujii et al. 2013), and they form halide complexes with anions like F-, Cl-and Br-(Rehkamper and Halliday 1999;Fujii et al.2013).It is essential to have all Tl+ions are oxidized to Tl3+,for Tl+cannot form ion complexes strong enough to entirely enter anion exchange resins (Nielsen et al. 2011; Nielsen et al.2017). Without full oxidation, Tl+would be missing,conducing to Tl isotope fractionation(Nielsen et al.2017).As shown in Table 3, the NVE-driven fractionation between aqueous Tl3+and aqueous Tl+can reach to about 23 ε-unit at room temperature.

So the youth remained quietly in the castle, eating and looking at all the beautiful things around him, and every now and then pretending to be searching busily in all the closets and corners

The difference of ε205Tl between aqueous TlCln3-nand aqueous TlCln1-n(n = 1,2,3,4)can be up to 7.8 at 25 °C.When the aqueous phase is ionized in the mass spectrometer,aqueous Tl3+or TlCln3-nwill change into Tl+ion.The NVE can cause about 20 ε-unit decline of ε205Tl at instrument operating temperature if the ionization process is incomplete.

Therefore, it should be noted that the NVE-driven fractionation in Tl isotope analysis would not be eliminated efficiently if the Tl+could not be completely transformed into Tl3+, or if Tl3+-complexes could not be completely inhaled via ionization.

4.2 The NVEs in natural processes

The NVE can take place in the process of exchange, segregation and migration processes of Tl. Such natural processes as the exchange between seawater and sediments,thermal alteration, phase transition, fluid metasomatism and large impacts have been observed to result in Tl isotope fractionations (Palk et al. 2011). The variation of ε205Tl for terrestrial samples is larger than 35 ε-unit(Nielsen et al.2017).For example,low temperature altered oceanic crust carries a deficit of205Tl (- 20 ε), and ferromanganese sediments carry an enrichment of205Tl(+ 15 ε) in the marine environment (Rehkamper et al. 2002;Nielsen et al. 2006b, 2013). The redox potential of Tl+to Tl3+is- 1.28 V.The oxidation state Tl()only exists at highly oxidizing conditions for terrestrial samples(Nielsen et al. 2017). The positive anomalies of ε205Tl(+ 4 ～+ 15) are thought to be caused by the transformation of thallium’s redox state during the exchange of Tl ion between hydrogenetic manganese oxide and seawater.This process is accompanied by NVE-driven fractionation(Peacock and Moon 2012; Nielsen et al. 2013). The adsorption simulation experiment found that Tl+could be absorbed into the vacancy site of oxygen tetrahedron structure in hexagonal birnessite, and Tl+could be oxidized to Tl3+at the same time (Peacock and Moon 2012).It has been discussed that the variation of ε205Tl between manganese oxide and seawater is dominated by NVE(Rehkamper et al. 2002; Koschinsky and Hein 2003;Schauble 2007;Nielsen et al.2017).In this study,we have used two structures of hexagonal birnessite with Tl3+added in the vacancy (Fig. 2), and calculated their fractionation factors driven by NVE relative to Tl+species in seawater (Tl+(aq) and TlCl(aq)) (Peacock and Moon 2012). In our simulation, we considered simulating the process of exchanging and oxidizing Tl+between seawater and manganese oxide as a long-time and equilibrium process.As shown in Table 4,205Tl tends to be enriched in hexagonal birnessite relative to Tl+species in seawater,and the NVE-driven fractionation can reach to 9.57 ε205Tl at 25 °C.This value provides an reasonable explanation for the positive anomalies found in ferromanganese sediments(Table 5).

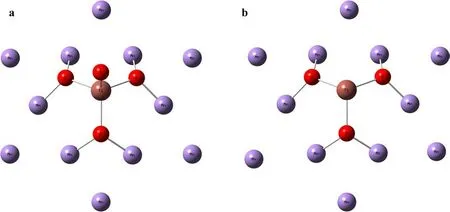
Fig. 2 a The structure of Tl_HxBir_pH8_2h; b The structure of Tl_HxBir_pH8_336h (Peacock and Moon 2012)

Table 4 NVE-driven fractionations(εN20V5 -203 =10，000·βN20V5-203)between two types of hexagonal birnessite and species in seawater

In addition,during the condensation process of the early solar system, Tl could exist in the form of diverse valence states at the high-T solar nebula.Total fractionation among Tl-bearing species was probably dominated by NVE when fractionation process reached equilibrium.According to the data in Fig. 4, the fractionation driven by NVE of Tl2O relative to Tl atom is 0.21 ε205Tl and the fractionation of Tl2S relative to Tl atom is 0.05 ε205Tl at 600 °C. The maximum value of the fractionation reaches to 7.93 ε205Tl between Tl+ion and Tl3+ion at 600 °C.As we can see that NVE-driven fractionation is not prominent among gas species at high-T. Also, if the process reached to phase equilibrium during the early stage of evaporation and condensation, the NVE-driven fractionation between two phases, such as Tl2S(g) to Tl2S(s) can reach - 0.49 ε205Tl at the condensation temperature of Tl (532 K). Therefore,only the NVE-driven fractionation cannot explain a 50-ε fractionation among meteorite samples,ranging from- 20 to+ 30 ε205Tl(Nielsen et al.2006a;Andreasen et al.2009;Palk et al. 2011; Nielsen et al. 2017). The uneven distribution of Tl isotopes in meteorite samples was resulted from the combination of stable isotope fractionation and the decay of the205Pb isotope. It is generally believed that the evaporation and condensation process in the early solar system is controlled by the process of kinetic isotope fractionation (Nielsen et al. 2017).

The abundance of Tl in CI chondrites is much higher than that in the mantle (0.14 ppm in CI vs. 0.0041 ppm in the mantle) (Palme 2014), which indicates that Tl is most likely to have evaporated into space or to have entered the core during the accretion of Earth. It has been known that Tl has an affinity with sulfur and Tl tended to enter the core along with sulfur during the process of core formation,according to the high Tl content of the sulfide (Coggon et al. 2009). This process would result in the Tl differentiation and isotope fractionation between mantle and core.Moreover, it has been measured that the partition coefficient of Tl in sulfide fluid/silicate melt equals to 4.1–18.8(Kiseeva and Wood 2013),indicating that sulfide is indeed the primary carrier of Tl in the mantle. Therefore,Tl is readily to be carried away by sulfide fluid and transported by magmatic fluid in the hydrothermal and partial melting processes (Nielsen et al. 2014). If Tl in mineral were partially removed as Tl2S by sulfide fluid, the equilibrium fractionation driven by NVE could reach- 4.83 to+ 1.86 ε205Tl at 300 °C, minerals including sulfides and silicates(Fig. 4). In the process of magmatic segregation, the fractionation of co-existing phases, silicate/sulfide is up to 1.96 ε205Tl (chalcopyrite/muscovite) at 1000 °C (Fig. 4).When measuring the natural minerals,205Tl was found to be enriched in sulfides. The silicate minerals, like micas and feldspar, have a deficit of205Tl (Rader et al. 2018). In experiments on the differentiation between sulfides and silicates, the fractionation of the co-existing phases can reach+ 0.2 to+ 0.3 ε205Tl at 1650 °C(Wood et al.2008).We have calculated the NVE fractionations between Tlbearing crystals, sulfides, sulfosalts, silicates, and Tl(Fm3m)(Fig. 4).The isotope fractionations driven by NVE of205Tl/203Tl range from 0.17 to 0.38 at 1650 °C between sulfides and silicates, which is consistent with the experimental data.

Fig. 3 The structures of Tlbearing crystalline compounds used for the calculation: Tl(Fm3m) (Olsen et al. 1994); Tl(Im3m) (Schneider and Heymer 1956); Tl2S(R3) (Mullen and Nowacki 1972); TlF(Fm3m)(Ketelaar 1935); TlCl(Fm3m)(Moeller 1933); Galena (Noda et al. 1987); Djerfisherite(Zaccarini et al. 2007);Orpiment (Mullen and Nowacki 1972); Sphalerite (Nitta et al.2008); Chalcopyrite (Knight et al. 2011); Muscovite(Richardson and Richardson 1982); Phlogopite (Hendricks and Jefferson 1939); Feldspar(Taylor 1934); Astrophyllite(Piilonen et al. 2003); Jarosite(Basciano and Peterson 2007)

4.3 The Tl isotope constraint on Earth's late veneer

Late veneer is a late accretion process which occurred after the core segregation. The contents of highly siderophile elements (HSEs) of the mantle were used to estimate how much material was delivered during the late veneer period(Day et al. 2007; Walker 2014).

By using the average Tl concentration of 500 ng/g for the continental crust, 200 ng/g for the oceanic crust and 0.7 ng/g for the mantle, the content of Tl in bulk silicate Earth (BSE) has been estimated to be about 3.03 ng/g(Shaw 1952; McDonough and Sun 1995; Salters and Stracke 2004; Nielsen et al. 2006c, 2014). If we assume that Tl would not enter the core during the process of core formation,which is based on the fact that the abundance of Tl is generally less than 0.02 ng/g in magmatic iron meteorites (Andreasen et al. 2012). We can also assume that the pristine mantle would be volatile-free after the accretion of proto-Earth, because of the highly volatile characteristic of Tl and the very low Tl concentration of current BSE relative to the chondrites and the similar Tl isotope composition between BSE and chondrites (Baker et al. 2010; Palk et al. 2018). Therefore, the very low content of Tl in the current BSE was almost entirely delivered by the late veneer.

Table 5 NVE-driven fractionations( =10，000·)of Tl-bearing minerals relative to Tl (Fm3m), calculated in this study

Table 5 NVE-driven fractionations( =10，000·)of Tl-bearing minerals relative to Tl (Fm3m), calculated in this study

The structures of minerals and crystals are taken from following references:Tl(Fm3m)(Olsen et al.1994);Tl (Im3m) (Schneider and Heymer 1956); Tl2S(R3) (Mullen and Nowacki 1972); Tl2O(R3m) (Sabrowsky 1971);TlF(Fm3m) (Ketelaar 1935);TlCl(Fm3m) (Moeller 1933);Galena (Noda et al. 1987);Djerfisherite(Zaccarini et al.2007);Orpiment(Mullen and Nowacki 1972);Sphalerite(Nitta et al.2008);Chalcopyrite(Knight et al. 2011); Muscovite (Richardson and Richardson 1982); Phlogopite (Hendricks and Jefferson 1939);Feldspar(Taylor 1934);Orthoclase(Viswanathan and Kielhorn 1983);Astrophyllite(Piilonen et al.2003); Jarosite (Basciano and Peterson 2007)

substance 0 °C 25 °C 100 °C 300 °C 1000 °C 2000 °C Tl (Fm3m) 0.00 0.00 0.00 0.00 0.00 0.00 Tl (Im3m) - 1.19 - 1.09 - 0.87 - 0.56 - 0.25 - 0.14 Tl2S - 1.88 - 1.72 - 1.38 - 0.90 - 0.40 - 0.23 Tl2O - 0.87 - 0.79 - 0.64 - 0.41 - 0.19 - 0.10 TlF (Fm3m) - 3.05 - 2.79 - 2.23 - 1.45 - 0.65 - 0.37 TlCl (Fm3m) - 2.96 - 2.71 - 2.16 - 1.41 - 0.63 - 0.36 Galena 1.04 0.96 0.76 0.50 0.22 0.13 Djerfisherite - 2.75 - 2.52 - 2.01 - 1.31 - 0.59 - 0.33 Orpiment 4.93 4.52 3.61 2.35 1.06 0.59 Sphalerite 2.59 2.37 1.89 1.23 0.56 0.31 Chalcopyrite 5.27 4.83 3.86 2.51 1.13 0.63 Muscovite - 3.88 - 3.56 - 2.84 - 1.85 - 0.83 - 0.47 Phlogopite - 3.39 - 3.10 - 2.48 - 1.61 - 0.73 - 0.41 Feldspar - 3.20 - 2.93 - 2.34 - 1.53 - 0.69 - 0.38 Orthoclase - 1.56 - 1.43 - 1.14 - 0.74 - 0.33 - 0.19 Astrophyllite - 3.07 - 2.82 - 2.25 - 1.46 - 0.66 - 0.37 Jarosite - 2.73 - 2.50 - 2.00 - 1.30 - 0.59 - 0.33

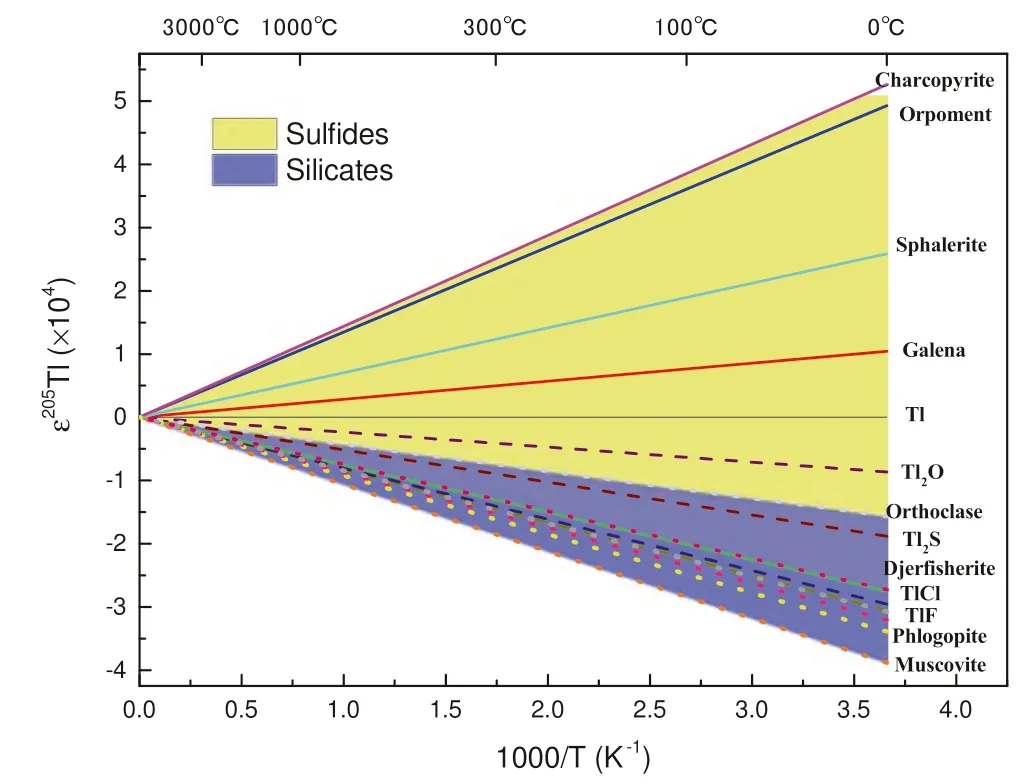
Fig. 4 Tl isotope fractionations driven by the nuclear volume effect for Tl-bearing crystalline compounds relative to Tl (Fm3m). The yellow area represents the results for sulfide minerals and the blue area represents the results for silicate minerals

In this case, considering the similar contents of Tl of enstatite chondrites (EC) and carbonaceous chondrites(CC)(Baker et al.2010;Palk et al.2011,2018)(Fig. 5),we use an average value (50 ng/g) to represent EC and CC.Meanwhile, the average concentration of Tl in ordinary chondrites(OC)is 6 ng/g(Andreasen et al.2009).We set x as the fraction of material from CC and EC delivered in the late veneer stage relative to the total mass of the Earth,and the fraction of OC is y. Previous HSEs estimate have suggested that the total value of late-stage substances accounts for 0.3–0.8 wt% of the total mass of the Earth(0.5 wt% on average). In that case, x + y = 0.5%. If we assume that the material of late-stage accretion had constituted the entire Tl of BSE (the concentration of Tl in BSE is defined as nBSE(ng/g)),then,50x + 6y = nBSEand nBSE= 3.03×67.4% = 2.04(ng/g),which is the observed value for BSE. If 0 ≤x ≤0.5%, because nBSE-= 44x + 3%, then we get 0.03 ≤nBSE≤0.25 ng/g,which is much smaller than the observed value of BSE,i.e.,2.04 ng/g (Fig. 6).The maximum value is only about onetenth of the observed BSE value. It means it needs more chondritic materials, especially CC and EC. When x is larger than 4.0%, nBSEcan be larger than 2.04 ng/g. The value can be close to the observed value 2.04 (Fig. 6).Therefore,the amount of 0.5 wt%late veneer is not enough to explain the Tl content in BSE.It needs at least 5 times of materials estimated by HSEs [i.e., 5 × (0.3 - 0.8 wt%) = (1.5 - 4.0 wt%)].

Fig. 5 The content of Tl and the Tl isotope compositions of the Earth and meteorite samples(Palk et al.2011;Baker et al.2010;Andreasen et al. 2009; Nielsen et al. 2006a)

Due to the high volatility of Tl, most of Tl was dissipated during the early Earth evaporation (McDonough 2014),and kinetic fractionation caused heavy Tl isotope to be left behind.The fractionation factor can be expressed as α, and α = (M1/M2)β, where β = 0.5 under vacuum. When the volatile species was Tl2S, then α = 1.0022, which would result in a 22-ε fractionation. However, such large fractionation has not been found between BSE and undifferentiated chondrites. On the contrary, Tl isotope composition of BSE is slightly lighter instead of becoming heavier.Considering the condensation temperature of Tl2S is only 523 K, it probably means that Tl could be completely evaporated during the early Earth,no matter it is in silicates or in sulfides.

Supposing that all of the Tl content in BSE came from the late veneer, it would be necessary for more chondrites to be added to the proto-Earth. We used the most massive abundance of CI chondrite as the upper limit of the Tl content (100 ng/g) (Baker et al. 2010). Then, the proportion of late veneer defined as klvcould be obtained from the following formula: 100 × klv= nBSEand nBSE= 2.04.Finally,klvequals to 2.04%which is about five times larger than 0.5% (Fig. 6). This result is consistent with the magnitude of late veneer suggested by the new SPH simulation (Marchi et al. 2018) and the oxygen isotopic evidence (Greenwood et al. 2018).

The Tl isotope composition in the BSE is slightly lighter than that in CC and EC (Fig. 5). As shown in Fig. 4,there is a about 2 ε-unit fractionation of205Tl/203Tl between the sulfides and the silicates at high temperature (1000 °C).Tl would be carried away as the sulfide in the mantle,leaving a lighter part into the silicate phase. This indeed suggests that there were sulfides occurred during the last stage of core segregation. The sulfides could be transferred and entered the core or at somewhere in the mantle that haven’t been found right now.Wood et al.(2008)believed that the metal phase would take away 50%of Tl from the BSE into the core. This process could lead to a deficit of205Tl/203Tl in silicate phase in modern BSE,which is about- 2 ε205Tl.If this is the case,there must be much more materials to be delivered to Earth than what previously estimated.

Fig. 6 The relation between the fraction of late-accreted mass of enstatite chondrites and carbonaceous chondrites(x)and the entire Tl concentration of BSE (nBSE)

5 Conclusions

In this study, an improved method was used for the first time to calculate the Tl isotope fractionation factors driven by the nuclear volume effect for Tl-bearing species,including ions, molecules, radicals, aqueous species and crystalline minerals. The improved method uses direct calculation of the effective electronic density instead of the contact electronic density. We found that oxidized Tl3+-bearing species are more enriched in heavier Tl isotopes that Tl+-bearing species. The maximum fractionation is 23.21 ε205Tl at 25 °C between Tl3+ion and Tl+ion. The fractionation between hexagonal birnessite with Tl in the vacancy and Tl+species in the seawater reaches 9.57 ε205Tl at ambient temperature.This fractionation value can adequately explain the enrichment of205Tl observed in the ferromanganese sediments.We find that Tl-bearing sulfides concentrate205Tl relative to silicates, and the variation ranging from 0.17 to 0.38 ε-unit at 1650 °C agrees with the results from the experiment of sulfide/silicate segregation.The change of redox state of Tl during the experiment can also lead to 20 ε-unit fractionation that is crucial in the study of Tl isotope fractionations. In conclusion, the nuclear volume effect of Tl isotopes plays an essential role in both natural and experimental processes, and our theoretical calculation provides a foundation for explaining the variations of ε205Tl in nature.

The Tl content and Tl isotope composition of BSE provides a constraint on the late veneer of Earth.We found that,based on the Tl content and its isotopic signal of BSE,the amount of materials delivered in the late veneer is more than five times than that estimated from HSEs. We also found that there is a sulfide-phase that occurred during the last stage of core segregation and may take away part of Tl to the core or deep mantle.

AcknowledgementsAll the calculations have been done on TianHe-2 supercomputer. Dr. Y.L. appreciates the funding supports from the strategic priority research program (B) of CAS (XDB18010100) and Chinese NSF projects (Nos. 41530210, 41490635).