气固两相流90°弯管抗冲蚀结构优化*
2019-09-06李岳鹏赫文博
黄 坤,邓 平,李岳鹏,廖 柠,赫文博
(1.西南石油大学 石油与天然气工程学院,四川 成都 610500; 2.舟山市港航和口岸管理局,浙江 舟山 316000; 3.重庆华润凯源燃气有限公司,重庆 400000; 4.浙江浙能温州液化天然气有限公司,浙江 温州 325000)
0 引言
由于过滤分离设备的能力有限,天然气在管道输送过程中会携带有少量固体颗粒[1],这些颗粒一部分来源于气田,另一部分则是由已有固体颗粒与管壁碰撞产生,微粒进入到管道内,与管输天然气一起形成气固两相流。考虑到颗粒的运动具有不规则性,颗粒必定会不断冲击管壁,造成管道的冲蚀磨损[2],尤其是弯管的磨损程度要比直管段严重得多[3-6],长时间的冲蚀磨损可能会导致管道的泄漏事故[7]。因此,如何降低弯管的冲蚀磨损程度,提高弯管的耐磨性能,保证天然气输送管道弯管的安全运行是一个十分重要的工程课题。
近年来,国内外学者针对如何提高管道壁面的耐磨性能进行了大量研究。Song等[8]研究了在直管内壁上添加肋条后管壁的磨损程度;Fan等[9]在直角弯管弯曲段外侧壁上添加了具有一定截面几何形状的肋条,并运用数值模拟技术计算了弯管壁面的冲蚀磨损速率;Pouraria等[10]针对海底管道,采用数值模拟的方法研究了T型管和标准弯头的冲蚀磨损程度;戚胜等[11]提出了一种弯头的替代结构,并对这种新型装置的流场特性和冲蚀磨损规律进行了数值模拟分析;王宇等[12]运用数值模拟技术研究了两种不同组合弯头内的气-固两相流动特征和管壁磨损特性,并根据数值模拟结果对组合弯头的结构进行了优化;Carlos 等[13]通过研究发现在弯头处添加涡流腔可有效缓解弯头的冲蚀磨损;季楚凌等[14]根据仿生学原理,对弯管内壁面进行了改进,并运用数值模拟技术研究了改进后弯管的冲蚀磨损情况。
以上研究大多是通过改变弯管的内部结构或者弯管的壁面从而优化弯管的耐磨性能,对于弯管管形优化的研究还比较缺乏,本文针对天然气输送管道气固两相流动的90°弯管,对其弯曲段进行三段式改进,利用COMSOL软件对三段式弯管弯曲段所对应的4个管形参数进行最优化处理,使用Fluent软件对优化后的三段式弯管进行冲蚀数值模拟并与一段式弯管的模拟结果进行对比分析验证了三段式的有效性,相关结论对今后弯管抗冲蚀结构的研究具有一定的参考价值。
1 三段式90°弯管设计
1.1 三段式90°弯管的提出
流体介质在流经弯管时由于速度的突变容易在弯曲段产生较强的二次流。二次流的存在会使弯管弯曲段的流线变得更加不规则,同时弯曲段流线的不规则状态还会传递到出口直管段。弯曲段流场变得更加复杂会使固体颗粒对管壁的碰撞变得更加频繁,进而造成更严重的冲蚀破坏[15]。由于二次流产生的位置主要分布在弯曲段以及出口段,因此改变弯管弯曲段的管形可以在一定程度上减小弯管中二次流的强度进而减小管壁的冲蚀磨损程度。参考文献[16]中的航空管路系统三段式弯管设计方法,本文提出了天然气输送管道的三段式弯管模型。
1.2 几何模型
以90°直角弯管为原型,在几何上保证进口直管段与出口直管段相互垂直的前提下,将原来的一段弯曲连接方式改进为三段弯曲连接方式。新的弯曲段由3个弯头组成,与进口直管段相连接的弯头称为第1弯头,其曲率半径为R1,弯曲角度为a;与第1弯头相连接的弯头称为第2弯头,其曲率半径为R2,弯曲角度为b;与出口直管段相连接的弯头称为第3弯头,其曲率半径为R3,弯曲角度为c。图1为三段式弯管的二维平面图。

图1 三段式弯管二维平面Fig.1 Two-dimensional plan of three-section elbow
2 三段式90°弯管优化
2.1 优化变量
根据前面建立的三段式90°弯管几何模型,若要确定管形那么需确定的参数包括:R1,R2,R3,a,b,c。假设第1弯头的曲率半径R1等于原一段式弯管的曲率半径,并且容易知道a,b,c存在如式(1)关系:
co=90°+bo-ao
(1)
因此只需要确定其中4个管形参数a,b,R2和R3即可。
2.2 目标函数
由于二次流主要发生在弯管弯曲段及出口段,所以本文将优化目标设置为:使弯管弯曲段的二次流平均值和弯管出口段的二次流平均值之和最小,即:
Minf(x)=Min(ξavg(w)+ξavg(c))
(2)
式中:ξavg(w)为弯曲段二次流平均值;ξavg(c)为出口段二次流平均值。
2.3 约束条件
首先,必须保证每个弯头的弯曲角度都大于0;同时,考虑到本文是对一段式90°弯管进行优化,为保证结构的合理性,各弯曲段的弯曲角度还应小于90°。
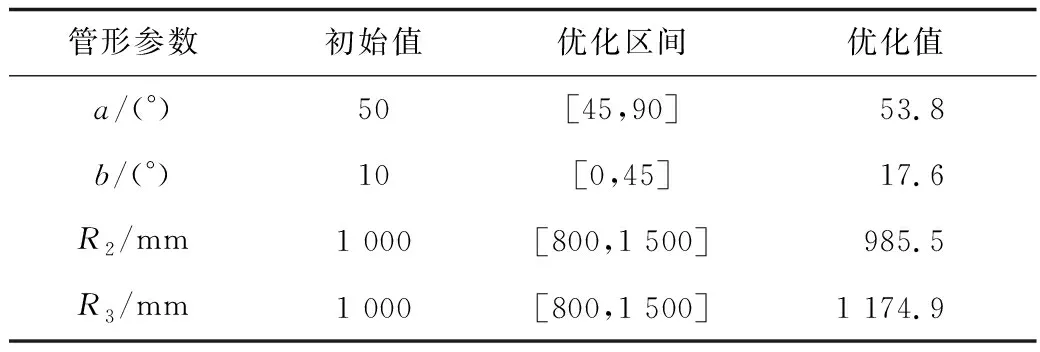
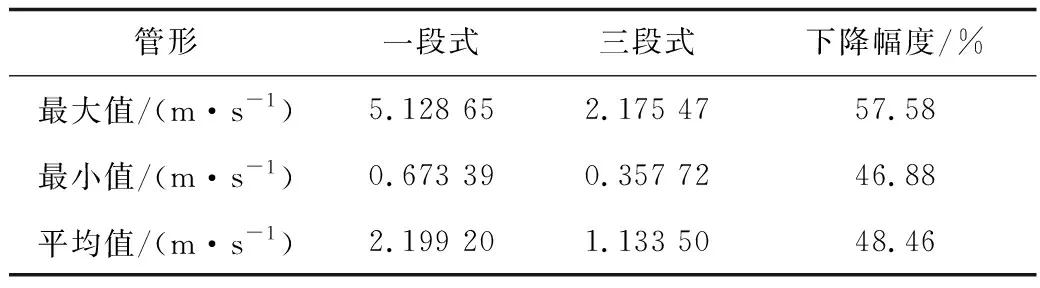
0° (3) 式中:a为第1弯头的弯曲角度;b为第2弯头的弯曲角度;c为第3弯头的弯曲角度。 根据GB/T 12459-2017《钢制对焊管件类型与参数》和某天然气长输管道的现场实际情况,本文将三段式弯管各弯曲段的曲率半径取值限制在区间[1.5D,6D]内。 1.5D≤R1,R2,R3≤6D (4) 式中:D为管道外径,mm;R1为第1弯头的曲率半径,mm;R2为第2弯头的曲率半径,mm;R3为第3弯头的曲率半径,mm。为了避免在进行管形参数优化过程中出现某些管形计算出来的二次流最大值过大或过小的情况,设置式(5)的约束条件。 (5) 式中:ξ1为一段式弯管的二次流最大值;ξ2为优化过程中三段式弯管的二次流最大值,其值在优化过程中是不断改变的。 COMSOL多物理场仿真软件提供了多种优化算法,主要包括:蒙特卡洛、Nelder-Mead,BOBYQA,COBYLA等。基于优化对象、目标函数及约束条件,在各优化算法中COBYLA的计算效果较好,而其他算法在优化过程中会偏向于计算局部最优,故本文采用COBYLA优化算法。 COBYLA算法也被称为线性近似约束优化算法,该方法首先通过假设f(xi),(i=1,2,…,m)是欧几里得空间Rn中1个非退化单极点处的函数值,为得到下1个变量矢量,对该极值点所对应的非线性目标函数和非线性约束函数进行插值,并将其看作线性问题进行近似计算[17]。 以直径400 mm弯径比2的90°弯管的优化为例,在COMSOL软件中直接建立如图2所示的三维模型(由于模型的对称性只需建立其中一半)。 图2 三段式弯管三维模型Fig.2 3D model of three-section elbow 定义弯管几何参数、流体参数和边界条件,并在软件中输入前面所叙述的约束条件、目标函数,采用可实现的k-ε湍流模型来模拟连续相的流动,最后利用COBYLA优化算法对三段式弯管的4个管形参数进行迭代优化,优化结果见表1,其中初始值是通过对不同网格数下的模型进行试算得到的接近于最优值的值。初始值的确定可以在一定程度上缩小迭代计算的区间,减小计算量。 表1 最优管形参数Table 1 Parameters of optimal pipe shape 优化后的管形尺寸为:管径D=400 mm,R1=800 mm,a=53.8°,R2=985.5 mm,b=17.6°,R3=1 174.9 mm,c=53.8°。 当流体介质流经弯曲段时会产生不同于主流速度方向上的二次流。二次流的形成是弯曲段管壁内外侧压力梯度和离心力共同作用的结果,属于主流流动引起的伴随流动。本文将二次流近似看成主流速度在各个截面上的速度分量,这样就可以通过比较各个截面上速度矢量的大小来判断该截面二次流的强弱。 根据文献[18]可知,弯管二次流最强的位置发生在弯曲段和出口直管段的接壤处。前文以弯曲段二次流平均值和出口段二次流平均值之和最小为优化目标,通过优化计算得到了最优管形,为了验证优化效果,对图3所示的A,B截面的二次流强弱进行对比。 图3 二次流强弱对比截面Fig.3 Compared cross sections of secondary flow intensity 表2 弯曲段出口截面二次流的最大值和平均值Table 2 Maximum and average values of the secondary flow of the exit cross section of the bending section 图4 A,B截面二次流速度矢量分布Fig.4 Distribution of secondary flow velocity vector at A and B cross sections 由表2可知,无论是二次流最大值、平均值还是最小值优化后的三段式弯管都远远小于一段式弯管,其中二次流最大值下降幅度最大为57.58%。从图4更能直观的看到二次流的最大值发生在近两颊壁面处,且三段式弯管截面处形成的二次流漩涡要小于一段式的。 为方便对比研究,本次冲蚀数值模拟共建立了4个弯管模型,如图5所示。其中一段式90°弯管模型共3个,管径D=400 mm,弯径比R/D分别为1.5,2,2.5;三段式弯管的几何尺寸根据3.1节的最优管形参数确定,4个弯管模型的进、出口直管段长度均取为15D。常温条件下,以天然气作为连续相,气体压力8 MPa,入口速度为16 m/s,从水平直管流入,从竖直向上直管流出,离散相的颗粒密度2 600 kg/m3,粒径10 μm,假设颗粒的初始速度与天然气相同,质量流量为0.001 kg/s。 图5 弯管几何模型Fig.5 Geometric model of elbow 以三段式弯管的网格划分为例,利用ICEM软件对三段式弯管模型进行网格的划分,网格均采用六面体结构化网格,并且对弯曲段的网格进行了加密处理,第一层边界层厚度设置为0.1 mm,增长率设置为1.2,网格划分情况如图6所示。 图6 三段式弯管网格划分Fig.6 Meshing of three-section elbow 整个弯管流域可被分为3个边界:进、出口以及管壁。对于连续相,湍流计算采用RNGk-ε湍流模型,进口设置为速度进口,出口设置为压力出口,湍流强度为5%,模拟中采用标准壁面函数法对近壁面区域进行处理。对于离散相,DPM模型中的进口和出口均设置为“Escape”,壁面设置为“Reflect”,且采用无滑移壁面。选用SIMPLE算法来计算压力-速度耦合,利用二阶中心差分格式和二阶迎风差分格式分别计算扩散项和对流项,残差均设置为10-5。本文中颗粒的碰撞模型选用碳钢材料的碰撞模型,冲蚀预测模型选用Oka冲蚀模型[19]。由于经过多次分离过滤后,天然气输送管道内气体所含固体量很少,所以在计算过程中忽略固体颗粒对连续相流场的影响,采用单相耦合的方法求解固体颗粒的冲蚀速率。 为验证本文所建立的冲蚀计算模型的有效性,对某气田集气站内的弯头进行仿真建模,结合该集气站的实际工况条件进行参数设置,将FLUENT冲蚀模拟的计算结果与现场检测报告进行了对比。所建立的90°弯头模型的管径D=76 mm,弯径比R/D=1.5,流动参数设置见表3。 表3 流动参数设置Table 3 Setting of flow parameters 数值模拟计算得出的弯头最大冲蚀率为6.541×10-8kg/(m2·s),根据2010年该集气站的检测报告,弯头的最大减薄量在1.2 mm左右,对应的最大冲蚀率为7.468×10-8kg/(m2·s)[1],误差在可接受范围内,因此,本文建立的冲蚀计算模型可以用来预测天然气管道弯管的冲蚀磨损情况。 图7所示为三段式弯管中心截面上的速度分布云图。由图7可知,入口直管段的速度分布比较均匀,当气流进入弯曲段后,速度分布发生了较大的改变:在第1弯头的内拱侧附近和第2弯头的外拱侧附近出现了速度的最大值,在第2弯头的内拱侧附近则出现了低速区,速度减小了很多,尤其是在第1弯头和第2弯头的交界处;第1弯头内拱侧的速度大于外拱侧的速度,而第2,第3弯头外拱侧的速度大于内拱侧的速度,同时可以看出,第2弯头内流场径向的速度梯度最大。随着气流进入出口直管段,截面上的速度梯度趋于缓和。 图7 三段式弯管速度云图Fig.7 Velocity nephogram of three-section elbow 图8为三段式弯管的冲蚀率云图。观察图8发现:三段式弯管的冲蚀磨损严重区域为第1弯头末端45°~53.8°靠近内拱两颊处以及第2弯头初始位置的内拱壁处。第3弯头的冲蚀磨损严重程度相比于前两段基本可忽略不计。表4给出了各个弯管模型的最大冲蚀率,其中三段式弯管的最大冲蚀率为2.41×10-10kg/(m2·s),该数值甚至比R/D=2.5的一段式弯管的最大冲蚀率3.08×10-10kg/(m2·s)还小0.67×10-10kg/(m2·s),因此,三段式弯管的局部耐磨性能得到改善。 图8 三段式弯管冲蚀率云图Fig.8 Erosion rate nephogram of three-section elbow 管形三段式弯管R/D=1.5R/D=2R/D=2.5最大冲蚀速率(×10-10kg·m-2·s-1)2.4111.14.613.08 图9展示了颗粒在三段式弯管和R/D=2.5的一段式弯管中的运动轨迹。观察图9(a)发现:当气体流经三段式弯管第1弯头时仅有少量固体颗粒与外拱壁碰撞并反弹至第1弯头末端附近两颊处;颗粒在第2,3弯头内运动十分顺畅几乎没有与壁面发生碰撞,这就造成了三段式弯管严重冲蚀的位置是在第1弯头末端附近的现象。对比图9(a)和(b)发现:在两者冲蚀最严重的区域,R/D=2.5的一段式弯管中的颗粒运动轨迹要更加混乱,可以看出三段式弯管流场的平稳性得到了较大的改善,固体颗粒能更加顺畅地流过弯管。 图10是三段式弯管和R/D=2.5的一段式弯管在Z=0 mm切面处的湍流强度云图,对比发现:三段式弯管内拱侧附近大部分区域的湍流强度在90%左右,而R/D=2.5的一段式弯管内拱侧附近的湍流强度达到了115%左右。局部湍流强度高会增强颗粒运动的无序性,加剧颗粒对壁面的碰撞。因此,三段式弯管的最大冲蚀率要小于R/D=2.5的一段式弯管的最大冲蚀率。 图9 颗粒轨迹对比Fig.9 Comparison of particles trajectory 图10 湍流强度对比Fig.10 Comparison chart of turbulence intensity 1)对D=400 mm,R/D=2的一段式90°弯管进行三段式改进,利用COMSOL对4个管形参数进行优化,最终得到4个管形参数的数值分别为:a=53.8°;b=17.6°;R2=985.5 mm;R3=1 174.9 mm。 2)优化后的三段式弯管流场更加平稳,弯曲段二次流的强度大幅降低,以一段式的截面A和三段式的截面B为例,二次流的最大值、最小值以及平均值分别从5.128 65,0.673 39,2.199 2 m/s降低到了2.175 47,0.357 72,1.133 5 m/s,下降幅度分别为57.58%,46.88%,48.46%。 3)Fluent冲蚀模拟结果表明,三段式弯管冲蚀严重的区域主要位于第1弯头末端45°~53.8°靠近内拱两颊处以及第2弯头初始位置的内拱壁处。三段式弯管的最大冲蚀率为2.41×10-10kg/(m2·s),比起D=400 mm,R/D=1.5,2,2.5的一段式90°弯管分别下降了约80%,50%,20%,其耐磨损性能大大提高。2.4 优化算法
3 优化结果及分析
3.1 最优管形参数的确定
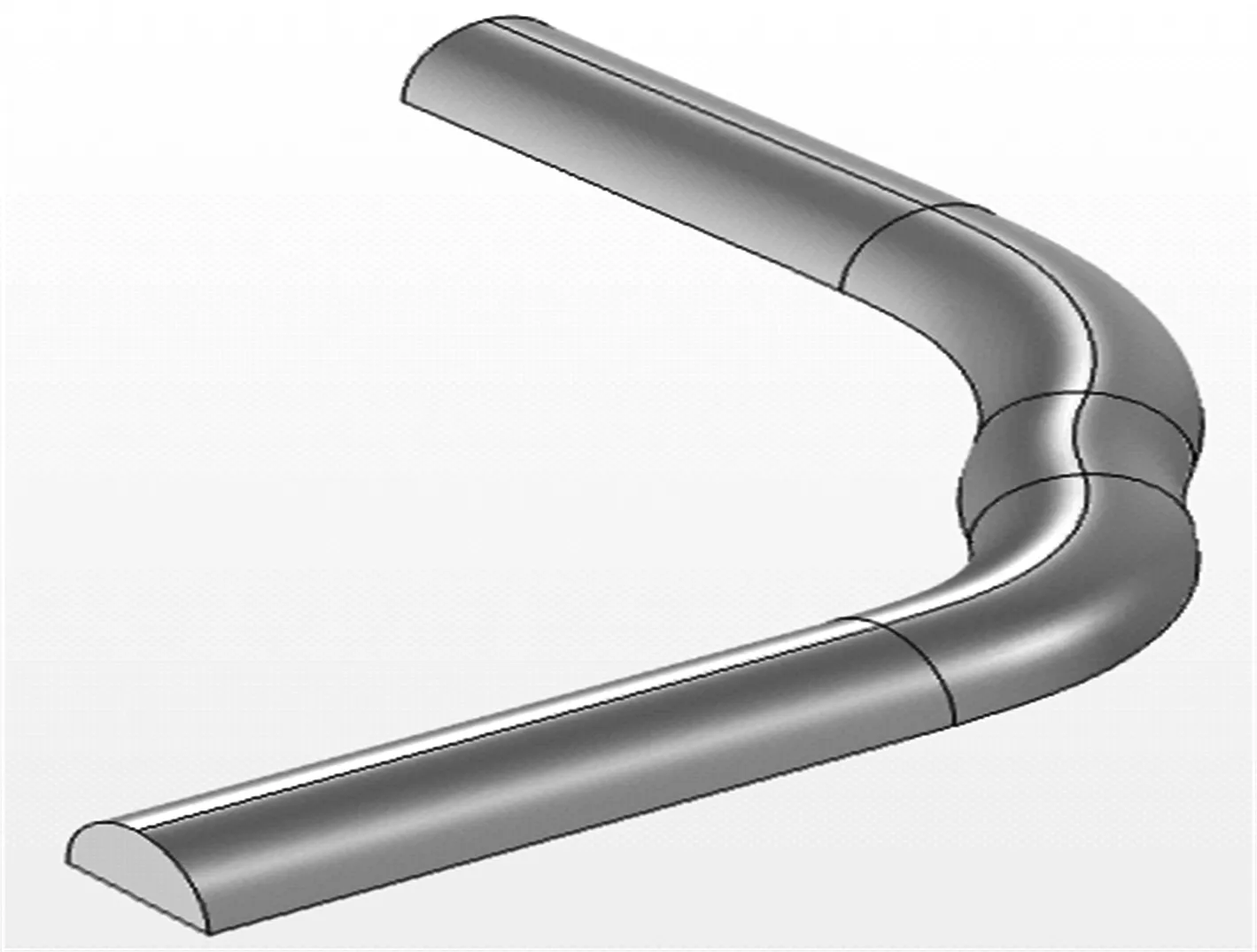
3.2 二次流大小的对比

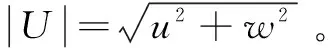
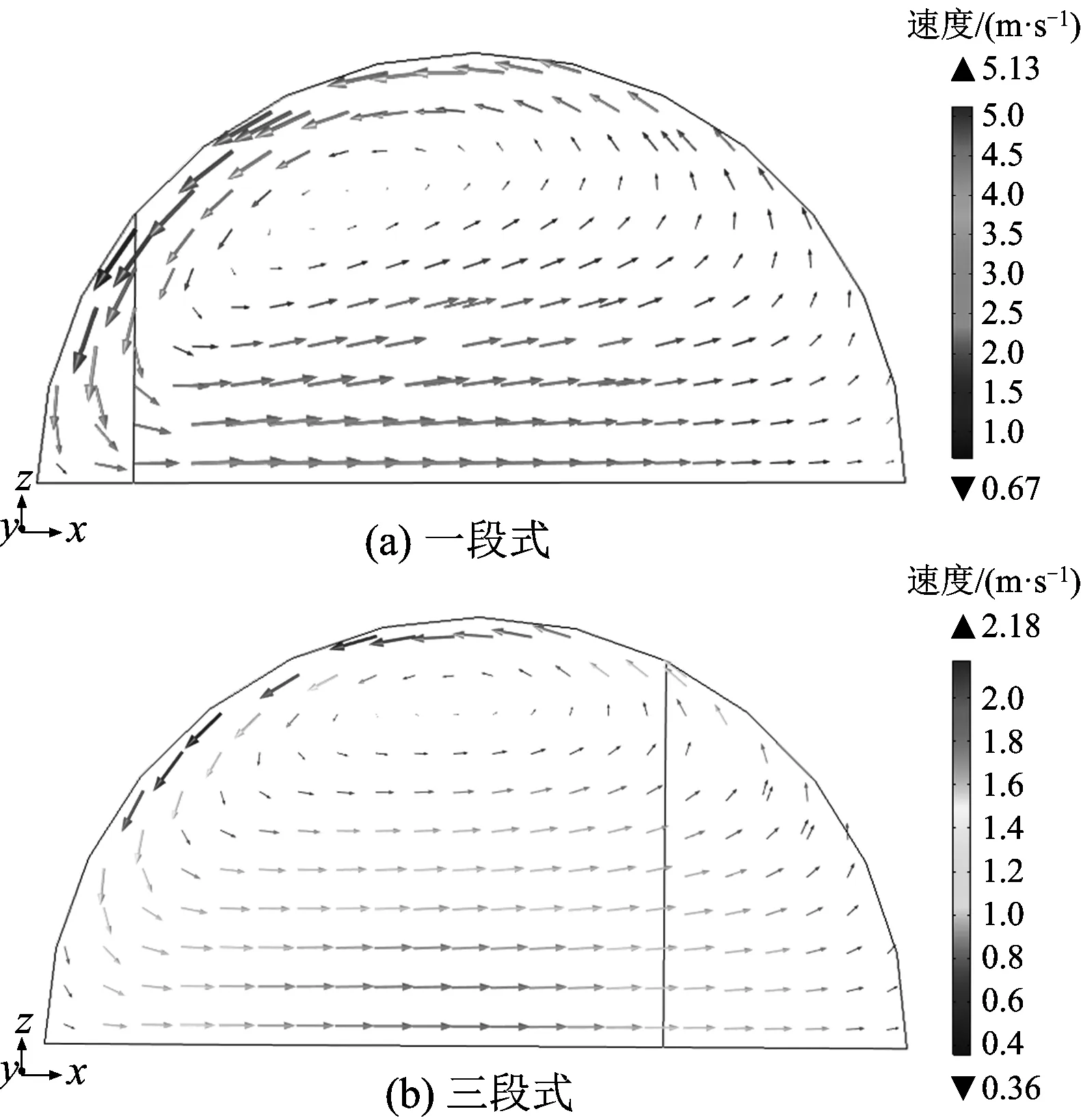
4 冲蚀数值模拟
4.1 管道参数
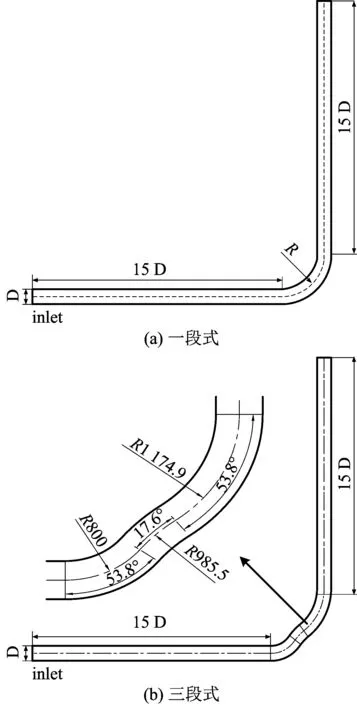
4.2 网格划分
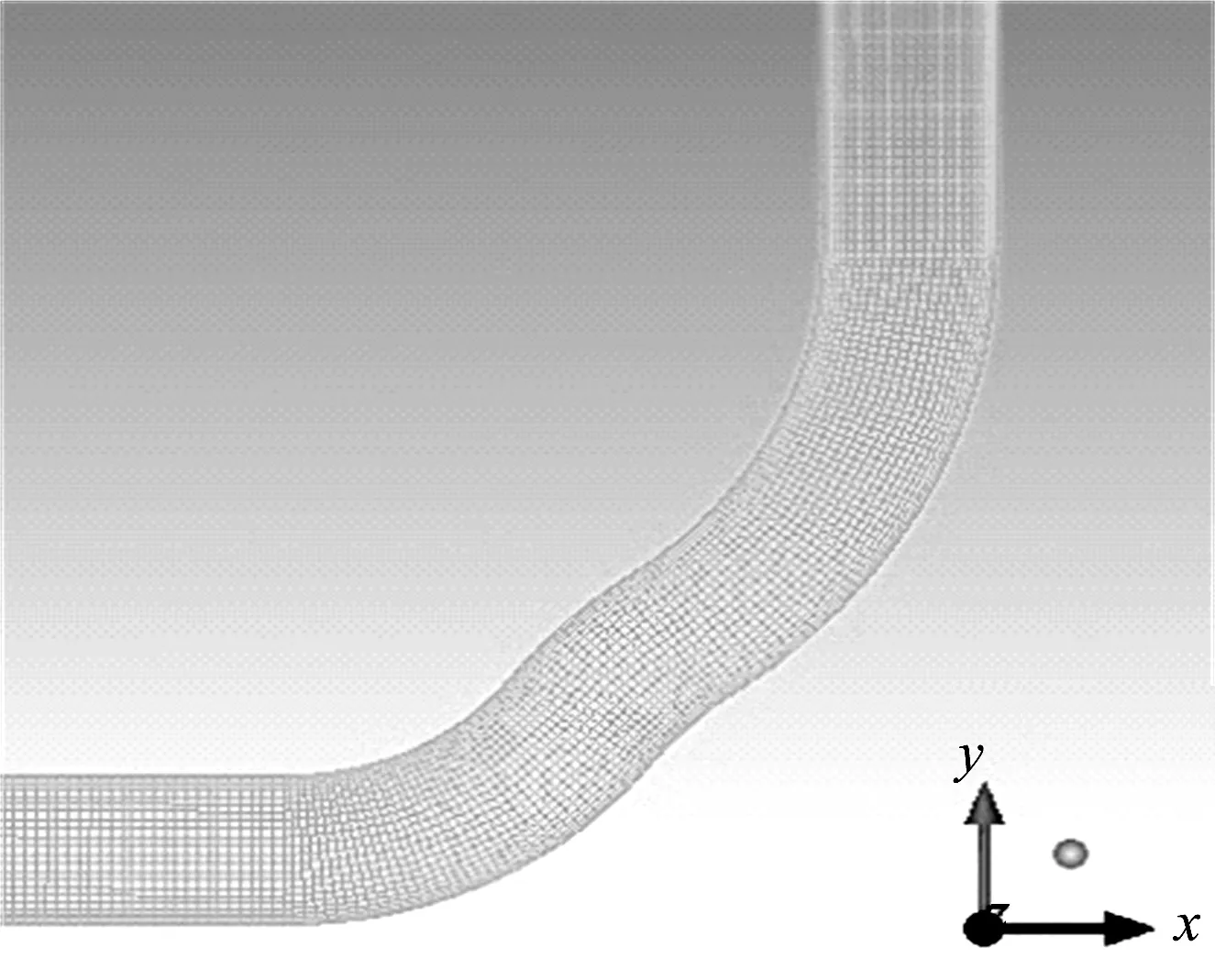
4.3 边界条件和数值算法
4.4 模型有效性验证

4.5 速度分布

4.6 冲蚀模拟结果分析




5 结论
