基于ANP-KL-TOPSIS法的铁路隧道围岩安全性评价

祁英弟，靳春玲，贡 力

(兰州交通大学土木工程学院，甘肃 兰州 730070)

0 引言

随着我国国民经济的发展，无论是铁路工程、公路工程还是水利工程等，隧道的开发建设越来越普遍。而在隧道开挖施工过程中，其岩体围岩的稳定及安全性一直是研究的重点和难点。影响围岩安全性的因素指标众多，各指标因素间相互关联、相互制约。因此，系统地识别出各影响因素并对围岩安全性进行评价预判，能有效控制隧道在施工开挖过程中的风险。

在隧道围岩安全及稳定性研究方面，苏永华等[1]利用非概率可靠性的凸集合模型对岩体结构围岩的稳定性进行了分析研究，该方法应用复杂不适用于常规围岩的安全性评价。康志强等[2]运用层次分析法结合可拓学理论建立物元评价模型，对地下隧道的岩体质量进行了评价，该方法没有考虑各指标因素间存在的关联影响关系，有一定的缺陷。郑颖人等[3]引入有限元强度折减法根据洞周位移及围岩塑性区大小对围岩安全性进行判别，其合理性有待进一步研究。常晓林等[4]利用联系熵模型对围岩稳定性进行评价，但并未给出准确的变形控制标准。王克忠等[5]采用数值仿真模拟方法对引水隧洞复合支护体系及围岩稳定性进行了研究，只提供了理论依据。我国在隧道围岩安全性研究方面，现有评价方法所考虑的影响因素固定片面，不能完整反映隧道围岩的安全状态，且计算量大，预设情况单一。评价指标体系及评价模型很不完善，有待进一步研究。

本文在既有研究的基础上更加全面的提出针对隧道围岩安全性的评价指标体系，应用ANP求解出影响隧道围岩安全性的各指标权重，解决了在各指标赋权时同一层次中不同影响因素之间存在的相互影响、相互依存关系。并将相对熵原理[6]与TOPSIS 法[7-9]相结合，用Kull-back-Leibler距离[10-11]计算所评价隧道各标段与理想值的贴近度。有效解决了单纯TOPSIS法对于正理想方案与负理想方案连线中垂线上的点无法区分优劣的缺点，使评价结果更加合理可靠。

1 建立隧道围岩安全评价指标体系

隧道的坍塌破坏，主要原因在于围岩稳定性差，安全性低。岩体质量问题复杂矛盾且影响围岩稳定安全性的因素众多，主要有地质因素、岩体自身结构状态及人为因素等等。根据《铁路隧道设计规范》、《铁路隧道超前地质预报技术规程》、《工程岩体分级标准》，识别出影响隧道围岩安全性的围岩岩性及结构特征、围岩物理力学性质、围岩地质特性及人为因素四类指标，建立如表1所示的隧道围岩评价指标体系及判定标准。

表1 隧道围岩安全性评价指标体系及判定标准

2 ANP-KL-TOPSIS安全评价模型

本文在传统TOPSIS法的基础上应用ANP法确定各指标权重，考虑了各指标因素间可能存在的关联和反馈关系，更加全面的考虑到了影响因素[12-13]。结合相对熵原理，将两个不同评价对象之间的差异用Kull-back-Leibler距离来衡量。综合运用ANP-KL-TOPSIS模型[14-15]对铁路隧道围岩进行安全性评价。ANP-KL-TOPSIS模型算法如下：

(1)建立标准化评价矩阵

假设有m个评价对象，表示为P={p1,p2,…,pm}，n个评价指标，表示为r={r1,r2,…,rn}。rij(i=1,2,…,m;j=1,2,…,n)表示第i个评价对象的第j项评价指标，建立初始评价矩阵R:

对R做标准化处理，得到标准化评价矩阵S:

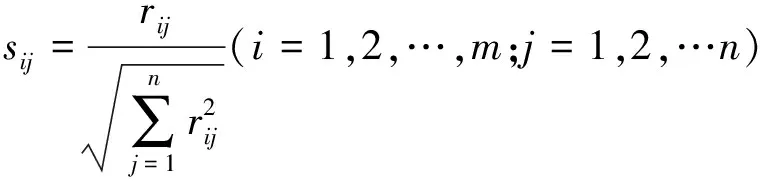
(1)

(2)ANP法确定指标权重

根据影响隧道围岩安全性各指标及其相互影响关系，构建ANP网络结构模型。

假设X1,X2,X3,…,Xm为ANP网络结构模型中的控制层元素，x1,x2,x3,…,xN为网络层元素组，ei1,ei2,ei3,…,ein(i=1,…,N)为xi中的元素。以Xs(s=1,2,…,m)为准则，xi(i=1,…,N)中的ejl(l=1,2,…,n)为次准则，将xi中的元素对ejl的重要度大小进行比较，构造出网络层间的判断矩阵，继而形成超矩阵子块Wij:

进而得到在以元素Xs为准则下的超矩阵W:

以Xs为准则，xi(i=1,…,N)为次准则，比较其他元素组对xi的优势度大小，得到归一化特征向量(p1j,p2j,…,pNj)T，将各个元素组特征向量组合得到元素组权重矩阵P:

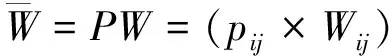
(2)

(3)建立加权标准化评价矩阵

tij=sij×Wj(i=1,2,…,m;j=1,2,…,n)

(3)

其中Wj表示第j项指标的综合权重。

(4)计算加权标准化矩阵T的正理想解和负理想解

(4)

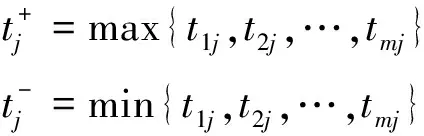
(5)

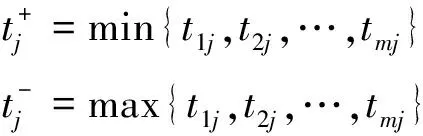
(6)

(5)计算与理想解的Kullback-Leibler距离

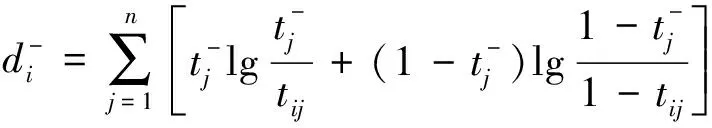
(7)

(6)计算各评价对象的相对贴近度

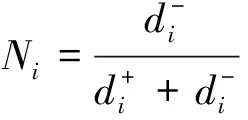
(8)

根据最终求得的各评价对象的相对贴近度Ni判定围岩的安全性，Ni越大，表明所评价对象离理想值越近，围岩越安全，反亦之。其中相对贴近度Ni大于0.8为安全Ⅰ，(0.6，0.8]为较安全Ⅱ，(0.4，0.6]为基本安全Ⅲ，(0.2，0.4]为不安全Ⅳ，小于等于0.2为极不安全Ⅴ。

3 应用实例

本文以新建张吉怀铁路兰新乡隧道进口段为例，说明ANP-KL-TOPSIS法在铁路隧道围岩安全性评价中的应用。

兰新乡隧道位于湖南省怀化市麻阳县兰新乡境内，沅麻红层盆地，为剥蚀丘陵地貌，地势起伏较大，地表植被茂盛。其隧址区山坡表层分布有第四系全新统、白垩系上统第二岩组，岩性主要为泥质砂岩，棕红色、褐红色，多有薄弱泥质夹层，为泥岩或泥质砂岩。隧道进口段全风化层风化较剧烈，多呈砂土状，厚约1～3 m；强风化层风化不均，厚约7～15 m，岩体节理裂隙发育，岩体破碎，多呈棱块状，敲击易碎，岩质较软。岩层产状主要为31°∠32°。隧道区地表水较发育，主要为河流水、溪沟水等。地下水类型主要为风化裂隙水及构造裂隙水(表2)。

根据兰新乡隧道工程地质勘查报告，经过整理分析得到表3所示的兰新乡隧道进口各隧道段围岩安全性评价指标数据。

表2 兰新乡隧道进口各隧道段特点

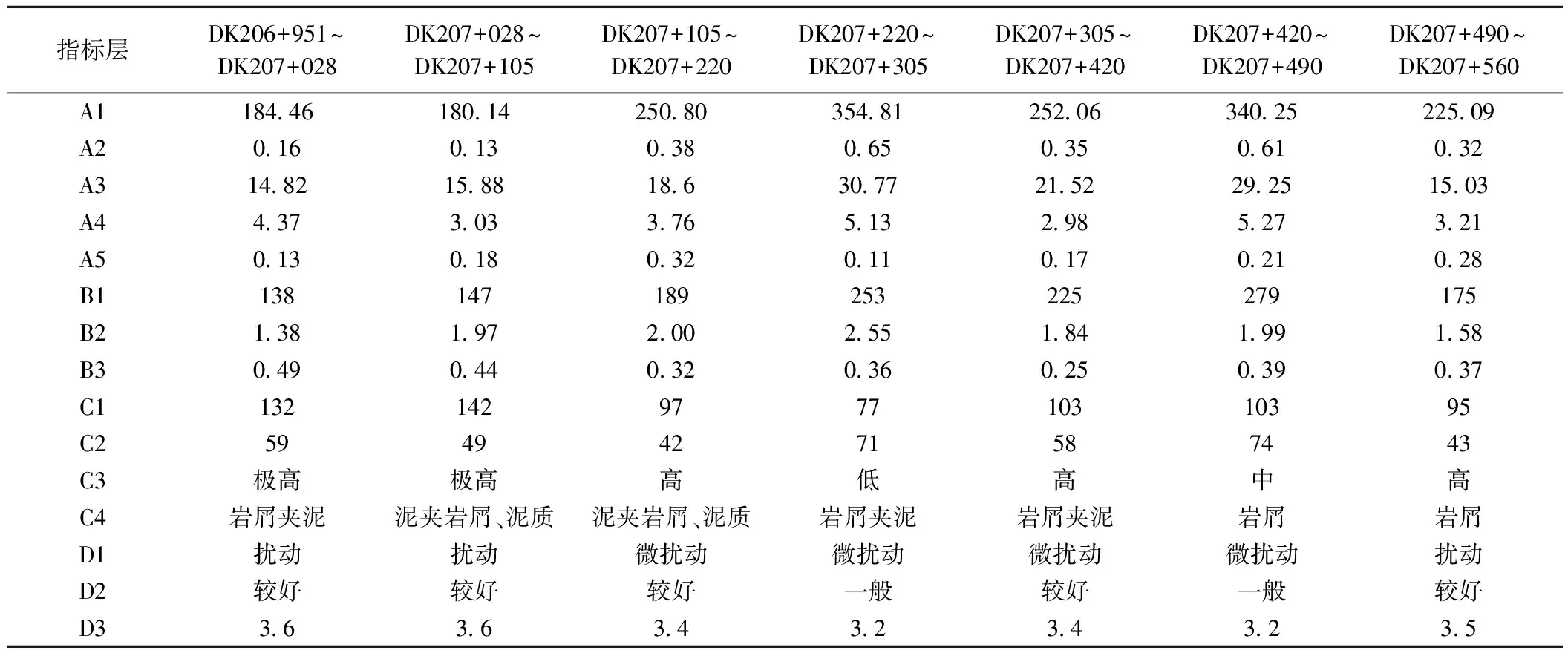
表3 兰新乡隧道进口各隧道段围岩安全性指标数据

将表1中识别出的15个因素指标进行关联影响分析，构造出各指标因素关联图如图1所示。

图1 指标因素关联图Fig.1 Correlation graph of indicator factors

对各因素指标进行相互重要度评判，构造未加权超矩阵，再对一级指标间的相互重要度进行评判，进而得到加权超矩阵如表4所示，在软件Super Decision中自动将加权超矩阵自相乘β次，待乘积收敛得到极限超矩阵如表5所示，最终得出各指标的综合权重。

由极限超矩阵可得各指标权重Wj分别为：

(0.119 4，0.104 3，0.099 6，0.078 3，0.063 6，0.056 7，0.051 6，0.053 9，0.015 5，0.072 3，0.086 5，0.046 8，0.068 4，0.061 1，0.022 1)。

通过KL-TOPSIS法计算最终得到各评价隧道段与理想解和负理想解的Kullback-Leibler距离及各评价隧道段的相对贴近度及所属围岩安全等级如表6所示。

表4 加权超矩阵

表5 极限超矩阵

表6 兰新乡隧道各隧道段围岩Kullback-Leibler距离与相对贴近度

表6中计算所得围岩安全等级与现场勘查评价结果基本相符。DK206+951～DK207+028及DK207+028～DK207+105隧道段的围岩安全等级为极不安全Ⅴ，该处围岩有高度的坍塌冒顶风险，施工中可采用小导管、径向注浆等措施防范风险，三台阶临时仰拱法施工。DK207+105～DK207+220、DK207+305～DK207+420及DK207+490～DK207+560隧道段围岩安全级别为不安全Ⅳ，有中度的坍塌掉块风险，施工中可采用小导管超前支护、三台阶法施工。DK207+220～DK207+305及DK207+420～DK207+490隧道段围岩级别为基本安全Ⅲ，可采用台阶法施工。

4 结论

(1)本文在既有研究的基础上，针对隧道围岩的安全性建立围岩安全评价指标体系。考虑到各指标因素间的关联影响性，运用ANP方法用Super Decision软件求出影响隧道围岩安全性的各因素指标权重。

(2)将相对熵原理与TOPSIS方法相结合以新建张吉怀铁路兰新乡隧道进口段的七处隧道段为评价研究对象，根据工程地质勘查报告，分析总结各段围岩安全性影响因素，用Kullback-Leibler距离最终求出各隧道段的相对贴近度，得出各段围岩所属安全等级。

(3)所得评价结果切合实际，对隧道施工有一定的指导意义。表明ANP-KL-TOPSIS模型能够克服各指标因素间的影响及对于正理想方案与负理想方案连线中垂线上的点无法区分优劣的缺点，得出可靠评价结果。该评价模型简单可操作，可运用于隧道围岩安全性评价中。