从《几何原本》看科学的传承
2019-09-05刘瑞祥
刘瑞祥
编者按:“读史使人明智,读诗使人聪慧,演算使人精密,哲理使人深刻,伦理学使人有修养,逻辑修辞使人善辩.总之,知识能塑造人的性格.”为了开拓同学们的视野,了解一些经典数学书籍,从本期开始,我们为大家奉上一些精彩的读后感,带你领略数学的魅力.
本期为大家介绍的是欧几里得的《几何原本》,经典图书中的经典,一起来看看吧.
若以理解大自然为志趣,并能世代相承、精益求精,则大自然的基本结构的至精至简、至善至美是可望可及的.
——项武义
我读《几何原本》的一个大的感受就是,科学是一项前仆后继的事业.这一感受是如此之深,甚至超过了我对其逻辑体系的感受.
事实上,只要稍微涉猎一点有关<几何原本》的科技史读物,比如读一读该书现代版本的前言、后记,我们就能体会到这一点.比如,据说早在欧几里得之前,泰勒斯就证明了“直径二等分圆”这一命题,并且泰勒斯还是几何证明的先驱,再有就是毕达哥拉斯学派对勾股定理(毕达哥拉斯定理)和“不可公度量”的发现,欧多克斯则研究了比例论并对“比例”重新定义.比例论就是因为“万物皆数(自然数)”的破产而产生的,正是因为“不可公度量”的发现,才使得希腊人原以为严谨的证明变得有漏洞了,因此产生了在新的比例定义和比例论基础上的证明.而正多面体显然和柏拉图有关.如此等等.
不仅如此,《几何原本》还对后世学者产生了深远影响.一个众所周知的例子是因研究平行公设而诞生的“非欧几何”.但这并不是因研究几何基础而产生的唯一成果.比如学者帕施等人,已经试图完善几何学的基础了.今天的数学家可以任意定义逻辑上無矛盾的体系,从而产生了各种各样的数学分支,希尔伯特第三问题则是针对极限法解决体积问题的,而在西方这种方法始于《几何原本》,高斯曾经思考过这一问题,最终是希尔伯特的学生德拜给出了结论.
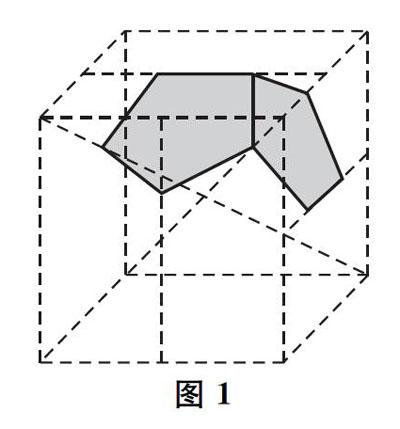
再以尺规作图为例,《几何原本》第四卷的命题十六“作正十五边形”显然已经涉及二元一次不定方程,即求满足方程5x +3y =l的整数,而尺规作图的判定性原则虽然已经由高斯等人解决,但还有其他方面的发展,比如进一步限定作图工具——单规乃至锈规、单尺乃至短尺等等,在正多面体方面,因为欧几里得原来的作法比较复杂,后世不断进行改进,中国清代学者梅文鼎用正方体简洁利索地作出正十二面体和正二十面体,如图1,可以称得上杰作.
除了以上所说以外,阿波罗尼奥斯研究圆锥曲线、阿基米德研究圆周率,以及后世学者对“黄金分割”、勾股定理的研究,都和《几何原本》有着密切的关系.而机器证明则可以说是从《几何原本》停下的地方出发的.《几何原本》还深深影响了牛顿、爱因斯坦,他们构建理论体系的方式,是和《几何原本》类似的.
(注:《几何原本》是世界上最著名、最完整且流传最广的数学著作,也是欧几里得最有价值的传世著作.欧几里得在<几何原本》中,系统地总结了泰勒斯、毕达哥拉斯及智者派等前代学者在实践和思考中获得的几何知识.欧几里得建立了定义和公理并研究各种几何图形的性质,从而确立了一套从公理、定义出发,论证命题得到定理的几何学论证方法,形成了一个严密的逻辑体系——几何学.而《几何原本》也就成了欧氏几何的奠基之作,它的出现,对人们的思维方式产生了深刻影响.)
