填充空间的多面体

常文武

编者按：同学们，看到盖房子用的长方体砖块，能够密不可分地结合在一起，砌出一堵堵墙来，你们有没有想过，如果把长方体砖块换成其他形状，还能不能盖出房子来呢？这其实就是多面体填充空间的话题，想了解更多内容吗？一起来走进下文，

用多面体填充空间是一个古老的话题.建筑用长方体砖块（如图1）是可以填充空间的最常见多面体.显然比长方体更特殊的正方体也是可以填充空间的.

风靡世界的乐高玩具（如图2）其实就是一些长方体的组合拼搭.而另一种著名益智玩具——索玛方块的基本元素则是正方体的单元，

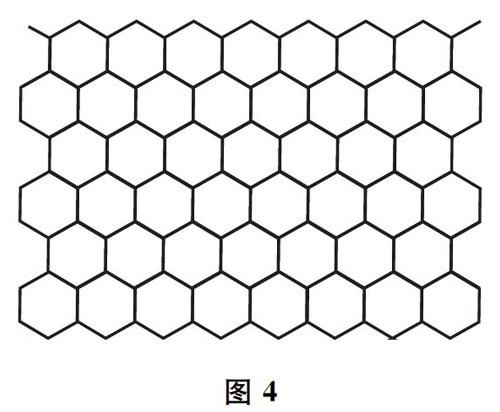
让我们观察广场上的地磚，如图4，常见的是一种正六边形的式样，就像蜂巢的截面.如果我们挖开一块，可以发现它就是一个正六棱柱，如果将这些正六棱柱的地砖一层层堆叠上去，就可发现正六棱柱能够填充空间.

以此类推，所有可以镶嵌平面的多边形一旦有一定厚度就可以填充三维的空间了，

以上都是很平凡的填充空间方案，不足为奇，

值得骄傲和自豪的是，中国人曾发现一种叫鳖膈的四面体是可以填充空间的.在《九章算术》一书中，古人用切割长方体的方法发现了它，这比西方人发现同一结构的时间（1925年）要早几百年.

鳖臑究竟长什么样？下面请读者跟我来制作几个把玩一番，

取一张A4纸，如图5，三等分后，裁掉其中三分之一，得到长宽比约为3：√2的长条纸，照着以下图6的步骤就可以完成一个鳖臑.

现在，请用三个鳖臑组合拼接成一个斜三棱柱（图7）.一旦成功了，鳖臑能填充空间的道理就不言自明了，

四面体是面数最少的多面体，下面利用“星化”正方体的方法产生一种能填充空间的新多面体——菱形十二面体，

将多面体的每个面尖锐化为一个棱锥而得到的多面体的过程就是“星化”.那么怎么将正方体星化呢？

想象一下单位正方体的中心（最长对角线的中点）关于正方体的6个面有6个镜像对称的像点，这些像点与原正方体的每个面构成的四棱锥就是该面上的星化锥.这6个正四棱锥加上原来的正方体共同组成的多面体就是一个菱形十二面体，如图8.为何是一个十二面体而不是二十四面体呢？注意到来自不同星化锥的相邻侧面恰巧平行于原正方体的某对角面.这样，原正方体的12条棱就融化成菱形对角线，24个面也就成为了12个面，

我们可以从正方体填充空间的特性自然推导出菱形十二面体填充空间的特性.

设想用无数小正方体组成如图9那样带空隙的三维空间.

图9只是无限空间的一个局部.这个空间里每个方块与周围12个方块以共棱方式邻接，但从不共面，也就是说这样形成的无穷大立体结构像海绵一样充满了洞洞眼.

现在让每个立方体在它的6个面上向周围的6个洞洞生出6个四棱锥，这样每个洞洞被它的上下左右前后伸出的四棱锥正好填满.这也就证明整个空间可以被菱形十二面体填满了.

如果允许填充空间的基本元素是两个，值得关注的一个例子是正八面体和正四面体的组合.

用一个正八面体和两个正四面体可以拼成一个平行六面体，而平行六面体可填充性是长方体可填充性的自然推论.

要证明图10中的多面体的确是一个平行六面体，关键要证明正四面体和正八面体邻接面融为一个面了.

分别算算两种多面体的二面角，可以发现它们正好互补：如图11，正四面体二面角的平面角等于菱形的一个锐角，而一个正八面体的二面角的平面角等于该菱形的一个钝角.

北京2008年奥运会游泳馆是二元组合填充空间的一个经典范例，这个有“水立方”美称的建筑用了两种多面体气囊来填充完成（如图12）.两种多面体以1：3的数量来配比，居一份的是十二面体，居三份的是十四面体，都不是正多面体，根据计算，它们对于空间填充的效率是很高的：把单位体积空间分割为固定数量的空间用的表面积最少.

在认识空间填充规律的进程中，自然界还有一种生物甚至超过了人类，这就是蜜蜂，蜜蜂创造的蜂巢的结构是半开放的菱形十二面体，据测算这样的结构耗费的蜂蜡最省.

本文介绍了多面体填充空间的几个例子.从面数较少的算起，有鳖膈四面体、正方体、4-8联合体、菱形十二面体、12-14联合体.当然还有更多的可填充空间的多面体，这就有待读者去发现研究了.