RTP非金属管道沿程水力摩阻计算研究
2019-09-05李晓伟霍富永朱国承矫捷何利民
李晓伟 霍富永 朱国承 矫捷 何利民
1中国石油大学(华东)
2西安长庆科技工程有限责任公司
全钢质管道强度高、可焊性好、易于连接,在油气运输过程中应用普遍.国内钢质管道集输油工艺计算软件和方法已经成熟,但实际应用过程中由于原油中溶解的酸性物质,会带来管道严重腐蚀[1].石油开采后期,水驱、聚合物驱导致原油含水率高、pH值低,由此带来的管道腐蚀严重.塔里木油田北部地区更换的钢制管道,部分管段不到一年就已腐蚀穿孔[2].非金属管道使用寿命长,耐腐蚀,保温效果好,结垢少,成本低(使用寿命30年以上),目前已在很多油田设计使用[3~5].
RTP管是一种高压塑料复合管材,由三层结构组成(图1),具有强度高、施工和连接方便、质量轻且无需防腐等优点,可用于中等管径和中、高压力油气输送管道工程.RTP管道于1995年6月第一次在英国投入使用,试运行后,Shell公司于1996年底在阿曼油田输油管线上正式使用内径150mm、长7 km的RTP管道.之后巴西石油公司、法国天燃气公司以及一些RTP制造商等多家单位发起了JIP联合工程项目,于2006年制定公布了RTP产品的国际标准,将RTP管全面推广应用于陆上油气开发、燃气输送及海上油气开发等领域[6].

图1 RTP管常见结构Fig.1 Common structure of RTP
1 RTP管道摩阻计算现状
非金属管道与钢质管道有质的区别.非金属管道的粗糙度远远小于金属管道(表1),一般为金属管道的10%~80%.

表1 常见管材内表面绝对粗糙度Tab.1 Absolute roughness of internal surface for common tubes mm
粗糙度低会带来管道运营过程中摩阻系数低,减少输送过程中泵提供的动力.同时,RTP管道与流动介质的接触特性也会影响摩阻的计算.粗糙度、接触特性带来的摩阻变化,需要进行特定理论分析或者由实验进行分析论证.
我国已于2010年确定了《非金属管道设计、施工及验收规范》[7-10].规范分为四部分:高压玻璃纤维管管线、钢骨架聚乙烯塑料复合管、塑料合金防腐蚀复合管、钢骨架增强塑料复合管.规范中建议供水管道压降参考式(1)计算
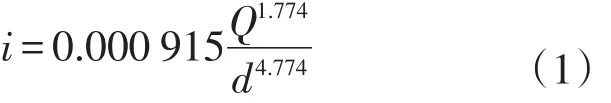
式中:i为水力沿程水力损失;Q为管道内流体流量,m3/s;d为管道内径,m.
然而,此公式未能体现出RTP管道由于粗糙度降低带来的沿途压降减小,同时其准确性并未进一步论证.
在工程上,计算水力压降多采用达西(Darcy)公式[11],认为粗糙度影响摩阻系数λ

式中:h为水力压降,m;λ为水力摩阻系数;L为管道水力计算长度,m;D为管道内径,m;v为管道内流体流速,m/s;g为当地重力加速度,m/s2.
在管道设计输量下,采用金属管道时,通常设计管内原油流动处于水力光滑区.当同一流量下,替换为同一管径的非金属管道时,管道粗糙度降低,但是水力光滑区的分界并不会随粗糙度减小而发生变化,摩阻计算公式仍应采用水力光滑区计算公式.
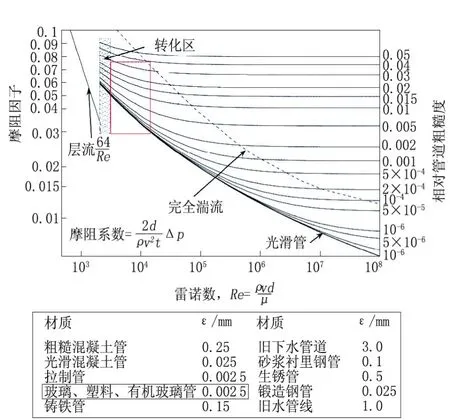
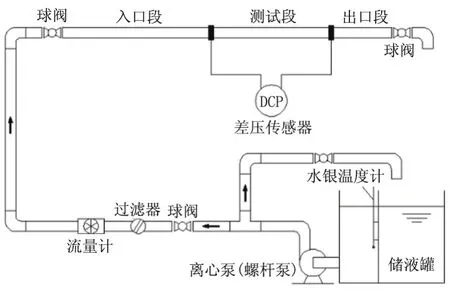
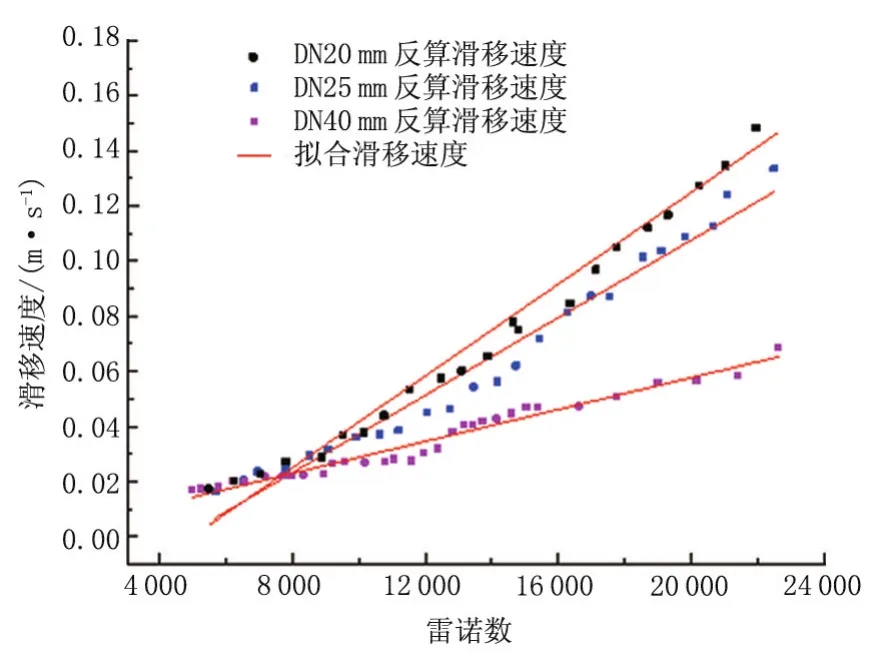
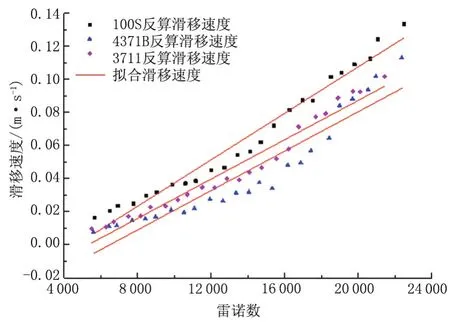
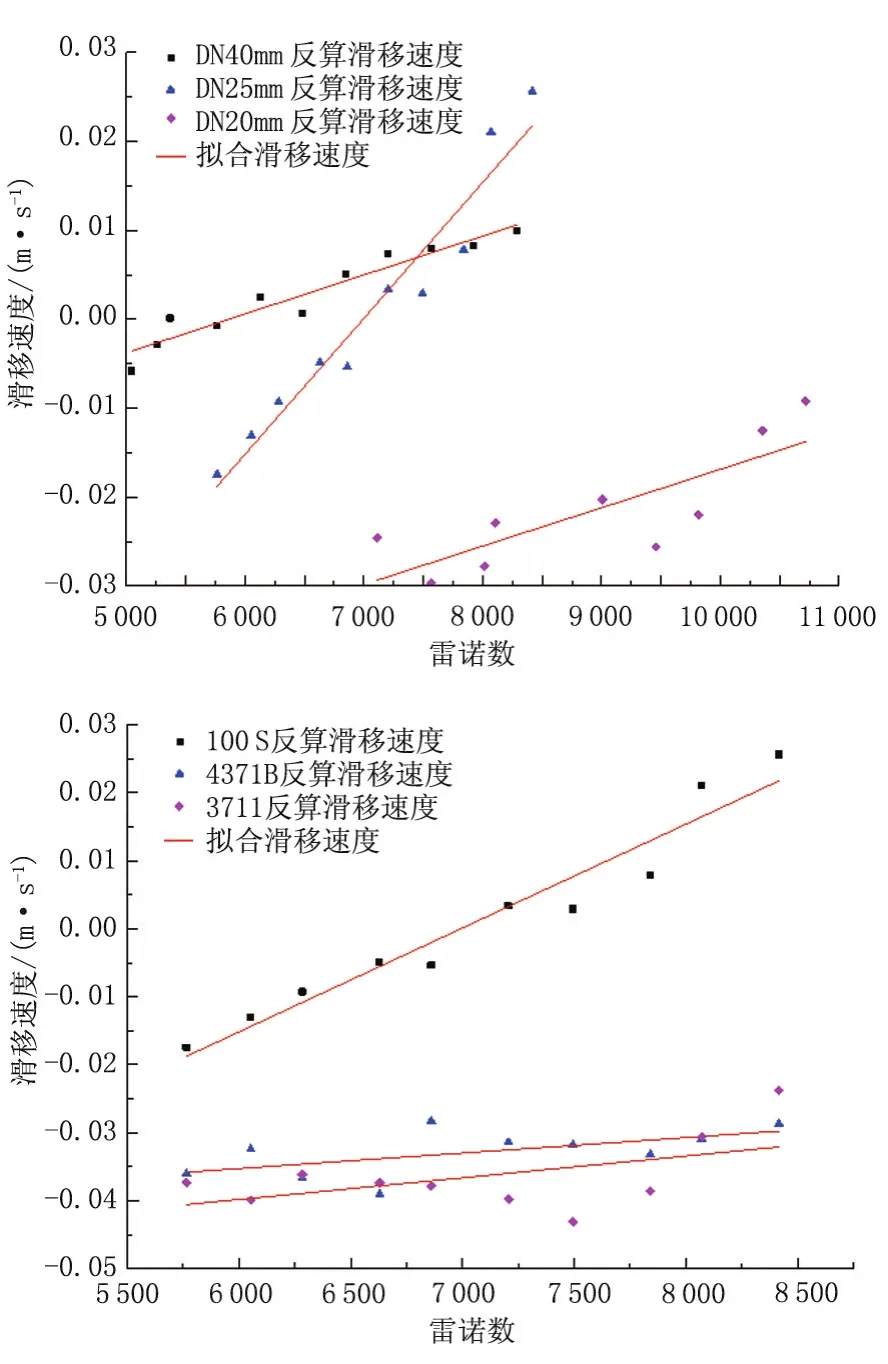
目前针对非金属管道的摩阻研究只有定性描述,从粗糙度低的角度结合莫迪(Moody)图(图2)说明非金属管道摩阻系数低.工业计算中,对非金属管道进行水力计算过程缺乏统一、准确的经验公式.如果流动处于水力光滑区,借鉴目前已有的水力光滑区摩阻计算的两个经典公式:波拉修斯(Blasius)公式(应用于4000 式中:Re为描述惯性力与黏性力之比的无量纲参数,在管流中反应流体流动与黏性力带来液体与管道之间的剪切力;λ为水力摩阻系数. 图2 莫迪(Moody)图Fig.2 Moody diagram 如果采用波拉修斯公式或普朗特-卡门公式求解水力光滑区的摩阻因子,可以看出摩阻因子不受粗糙度的影响.2010年规范中的公式实质上是达西公式和波拉修斯公式的结合,也无法描述非合金管道粗糙度带来的摩阻系数减小.从莫迪图(图2)可以看出,处于水力光滑区的摩阻系数接近,但是依旧存在差异. 因此,从理论上提出适用于RTP管道的更为准确的半理论公式,更准确地计算沿程压降,为工程提供更为准确的非金属管道沿途压降计算准则,成为RTP管道内流体流动特性的研究重点. 为进一步确定RTP管道摩阻特性,尝试从理论方面建模,以波拉修斯公式为基础,分析无量纲摩阻修正量,采用实验结果,提供不同油品在RTP管道中流动过程摩阻修正参数,完善RTP管道摩阻计算模型[12-13]. 波拉修斯公式考虑到建模过程中包含低粗糙度带来的影响,而未考虑介质与管道壁面接触特性导致速度滑移带来的摩阻变化,因此在后续建模过程中考虑滑移因素带来的影响.流体流动过程中的速度滑移如图3所示. 图3 层流时流体与边界滑移示意图Fig.3 Sketch diagram of slippage between liquid and boundary in laminar flow 因此,建模过程中增加对滑移速度的描述,对流动过程中的摩阻进行建模.摩阻建模过程,以波拉修斯公式为基础,增加相对滑移速度u0的影响. 在管道壁面性质一定条件下,滑移速度与管道内流体速度和速度梯度有关,引入滑移速度计算公式u0=u0( R e).滑移速度中的雷诺数( R e)采用流体截面平均速度进行计算 式中:uˉ为管道内流体平均速度,m/s;D为管道水力直径,m;ν为流体黏度,m2/s. 由于考虑滑移带来的影响,使用流体平均截面速度与流体边界滑移速度的差值替代无滑移时的速度进行求解.首先求得流体与流体边界相对速度uc 式中:uc为管道内流体与流体边界的相对速度,m/s;uˉ为管道内流体平均速度,m/s;u0为流体边界与管道壁面之间的相对滑移速度,m/s. 计算过程的雷诺数也以相对速度为基础 式中Rec为使用管道内流体与流体边界的相对速度uc计算得到的雷诺数. 摩阻系数的形式参考波拉修斯公式基本形式 式中λc为以相对滑移速度雷诺数计算得到的水力摩阻系数. 2)水分管理。机插后浅水护苗,活棵后露田2~3天,以后浅水勤灌,当总苗数达到预定苗数80%时开始晒田,达到田中不陷脚,叶色褪淡,叶片挺起为止。晒田复水后,保持干湿交替,在孕穗及抽穗扬花期保持浅水层,收割前5~7天断水。 进而以滑移速度为基础,采用达西公式计算水力压降hc 式中:hc为水力压降,m;L为管道水力计算长度,m. 通过上述体系,可以完成存在滑移时水力摩阻的计算.但是对于滑移速度u0,并未找到合适的关系描述,使此模型封闭.为进一步了解流体在RTP管道流动过程中,由于表面性质可能会产生一定的速度滑移现象而对摩阻存在影响,尝试通过实验数据确定合理的计算滑移速度的关系式. 为进一步确定不同油品在不同非金属管道内流动的摩阻性质,在室内搭建图4所示实验管路,对流动过程沿程摩阻计算公式进行优化.测试管道长9 m,管道外套有绝热层,尽可能保证流体流动过程中温度变化在可接受范围内. 图4 实验管路示意图Fig.4 Sketch diagram of experimental flow line 实验过程采用水、黄岛原油为实验介质,使用德国Anton Paar旋转黏度计对介质黏度进行测量,使用SY-05型石油密度计对介质密度进行测量. 测试管道选取3种非金属管道,管道材质型号分别为4731B、3711、100S.这3种材质有不同特点,其中4731B为进口PERTO材料,具有较好的耐热性;3711为国产PE第一代材料;100S是国产PE1.5代,PE中加入了改性剂,耐温性较好.实验前,使用水和黄岛原油对流体在实验管道内表面的附着性进行测试,得到金属管道内表面具有亲水疏油性,3种非金属管道内表面均具有亲油疏水性. 在实验过程中,调整储液罐内的加热丝,水为工作介质时,保证储液罐内温度恒定于20℃±0.1℃;黄岛原油为介质时,保证储液罐内温度恒定于17℃±0.1℃.通过设备测量黏度-温度曲线、密度-温度曲线,分析合理性后,确定流动设计工况的工作点的密度和黏度.实验当地重力加速度为9.807 m/s2. 首先以水为介质进行实验.实验过程保证储液罐温度稳定在设计温度,流动稳定后测得压降.为分析非金属管道管径对摩阻的影响,以100S材质为基础,管径分别为DN20mm、DN25mm、DN40mm进行实验.通过达西公式和波拉修斯公式反算速度滑移量,得到滑移速度与雷诺数拟合关系,如图5所示. 图5 不同管径下滑移速度与雷诺数关系(水为工作介质)Fig.5 Relation between slip velocity and Re number for different pipeline Relation between diameter(flow medium:water) 管径为DN40 mm时 管径为DN25 mm时 管径为DN20 mm时 由于实验过程中采用的管径数据有限,难以确定u0与Re之间的系数在不同管径中的计算方法. u0与Re之间呈线性关系的原因,一定程度上是由于在管道稳定流动水力摩阻计算过程中,雷诺数表现为惯性力与黏性力无量纲比、与流动速度呈线性相关;而滑移速度一定程度上与管道边缘速度梯度线性相关.在管道一维层流流动中,可以认为,.结合管道内径给定,可以得到u0与uˉ线性相关,进而得到u0与Re线性相关.然而实际过程中,由于流动并非一定处于层流区,u0与Re线性关系需要进一步论证. 为探究不同材质的RTP管道对管道内流动摩阻的影响,采用管径为DN25 mm的4371B、100S、3711共3种材质的管道进行实验.由于不同材质的RTP管道表面性质差异,管道内流动过程中不同的滑移效果会带来不同的摩阻因子.类似之前处理,倒推得到滑移速度,如图6所示. 图6 不同材质下滑移速度与雷诺数关系(水为工作介质)Fig.6 Relation between slip velocity and Re number for different material(flow medium:water) 通过对比可以发现,同一管径、不同雷诺数条件下,由于管道内表面性质存在差异,会存在不同的计算滑移速度.通过数据可以看出,不同RTP管道材质可能会导致不同的滑移速度.因此,在使用RTP管道之前,需要对此管道表面性质进行研究,确定合理的计算公式. 为了进一步研究原油在RTP管道中的摩阻计算方法,采用黄岛原油,以类似的实验方法和计算模型,分析黄岛原油为实验介质时的滑移模型摩阻计算参数. 同样,以材质为100S不同管径的RTP管道,材质不同的内径为DN25 mm的RTP管道,分析黄岛原油为介质的流动中管径、材质对滑移速度与雷诺数关系的影响(图7). 通过图7可以看出,滑移速度与雷诺数之间的线性关系比较明显,不同材质内表面会导致计算滑移速度与雷诺数之间存在不确定影响.在水力光滑区,可以通过一定量实验数据,完善滑移速度计算经验关系式,进而使用计算滑移速度模型求解摩阻系数. 图7 管径、材质对滑移速度与雷诺数关系的影响(黄岛原油为工作介质)Fig.7 Effects of diameter and material of pipe on relation betweenslipvelocityandRenumber(flowmedium:Huangdao crudeoil) 可以发现,在原油为介质的实验中,存在反算滑移速度为负数的情形,以水为介质的实验中反算滑移速度均为正数.这种现象的发生可能是与RTP管道的疏水亲油性有关.由于RTP管道疏水性,水与管道之间滑移剪切力大于水与管道之间黏性力.RTP管道的亲油性会导致管内流体流速较低时,雷诺数较小,管道与原油之间的黏性力大于滑移剪切力,导致反算滑移速度为负数.当流速较高时,黏性力小于滑移剪切力,反算滑移速度为负数.同时,由于建模过程中没有考虑流体与管道之间黏性力的影响,因此在实验过程中应当以黏性力远小于滑移剪切力的部分提供滑移速度计算经验关系式,以增加拟合经验关系式的准确性. 目前并未形成公认的适用于RTP管道的水力摩阻计算方法.本文尝试从流体与管道内壁发生速度滑移为基础建模求解,以实验确定经验关系式,在一定程度上为RTP管道水力摩阻计算提供参考. (1)在水力光滑区,管径一定的情况下,计算过程采用的滑移速度与雷诺数呈线性相关,并且线性系数因流体性质、管道内壁性质而产生差异.本文提出的滑移速度摩阻计算模型需大量实验数据,以完善不同油品在不同类型RTP管道中的计算参数.由于实验过程采用的管道数量有限,未能给出管径对滑移模型计算线性相关系数的影响,后期需要增加实验数据以便对模型经验关系式进行完善. (2)RTP管道材质多种多样,管道内表面疏水亲油性质会导致在一定范围内增加输油过程的摩擦力,无法达到使用RTP管道减阻的目的.当流体与管道内壁黏性力大于滑移剪切力时,反算滑移速度为负数.在设计过程中,需要对采用的RTP管道表面性质有直观认知,选用合适的材质,最大程度地节能降耗,减小流体在管道内的流动阻力. (3)在RTP管道以水为介质的实验过程中滑移速度均为正,因此在RTP管道设计过程中可以考虑对内表面进行特殊处理,增强其疏水疏油性,保证流体流动过程中管道与流体间滑动剪切力远大于流体与内壁的黏性力,从工艺设计上降低管输过程中的水力摩阻.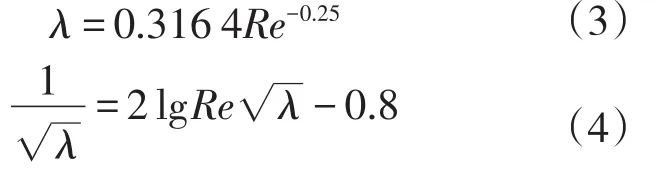
2 RPT管道摩阻计算模型的建立




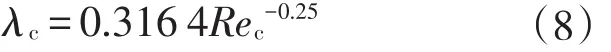
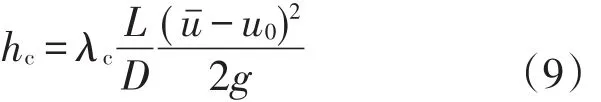
3 RPT管道摩阻实验
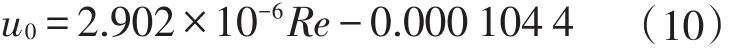
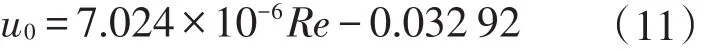
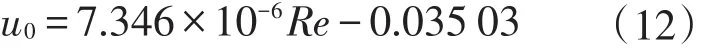
4 结论
