一种基于连通原理的射频发射覆盖范围近似表示

吴思远

(中国电子科技集团公司 第二十研究所， 陕西 西安 710068)

有多种原因会造成数据电台组网通信系统中两台电台通信中断，常见情况多为通信系统故障原因[1]，如发射电台功放故障[2]，接收电台接收通道故障，或者在时分复用通信系统中，收、发电台时间不同步[3]，或者是有两台电台同时向另一台电台发送消息造成多径干扰[4]，等等。但是，在实际通信系统中，在不考虑衍射、反射、透射的前提下，若从发射电台到接收电台的直线上存在障碍物，空间中传输信息的电磁波会被障碍物完全吸收，接收电台无法接收到通信信号，导致通信中断。空间遮挡导致通信中断方面的研究，对于飞机航路规划[5]及通信站点位置选址[6]等具有重要的实用价值。

目前，空间遮挡也会导致通信中断相关方面的研究却往往被忽视。本文研究在数据电台组网通信系统中，由于障碍物遮挡引起的通信中断问题。在不考虑反射、透射和衍射情况下，利用连通性方法，给出导致通信中断的条件，并在获知发射电台定位信息、电台最大传输距离及接收电台海拔高度的前提下，在平面地图上绘制发射电台射频发射覆盖区域。

1 数学模型

为了计算的便利，假设地球是一个标准的球体，其半径为R=6 371.393 km，并建立地球空间直角坐标系如图1所示。其中，O点为地球球心，X轴由地球球心指向本初子午线与赤道的交点，Y轴由地球球心指向东经90度线与赤道交点，Z轴由地球球心指向北极点。

图1 地球空间直角坐标系

假设M为东经、北纬四分之一半球上任意一点，M′是M在OXY平面上的投影点，M点的经度为LM，纬度为BM，海拔高度为HM，则在地球空间直角坐标系下，M点的坐标与其经度、纬度和海拔高度的关系为

(1)

2 理论分析

在不考虑反射、透射和衍射情况下，电台发射信号沿直线传播，如果有障碍物存在，则可能导致通信中断。为了研究发射电台的射频发射覆盖范围，即使较小的覆盖区域，也很难遍历所有的点去确定它们和电台发射点之间的连通性。因此，采用选取离散点的方法去进行遍历，本文选择以发射点的方位角步进的方式进行遍历。在同一个方向上，以覆盖目标点和发射点与地球球心夹角步进方式进行遍历。假设最大发射距离为Dmax，目标点的海拔高度固定为H，方位角和中心角的步进均为0.1°，则第一个目标点选择为发射点正北方向，且与地心距离为R+H、与发射点距离Dmax的空间一点。假设第一个目标点和发射点分别与地心连线的夹角为θ，则第二个目标点选择为发射点正北方向，与地心距离为R+H，且该点和发射点分别与地心连线之间的夹角为(θ-0.1)，依此类推，直到目标点和发射点与地球球心的夹角小于0.1°为止。然后，类似地在北偏东的方向上，按同样0.1°步进的方式进行遍历，直至所有方向上都遍历完成。由于目标点海拔高度恒定，因此，在一个方向上，当一个目标点与发射点连通时，可以不再遍历该方向上距离发射点更近的目标点，因为更近的目标点一定与发射点连通，只有当目标点与发射点不连通时，才去遍历下一个离发射点更近的目标点。根据以上策略，在每个方向上都能得到一个距离发射点最远的可连通的目标点，将相邻方向上可连通的最远目标点相连接，所构成的区域便是所要表示的射频发射覆盖范围。

2.1 连通性原理

在确定了发射点和目标点的位置后，需要判定发射点与目标点的连通性。假设发射点为S，目标点为D，P是S与D连线上的一个判定点，如图2所示。

图2 连通性判定示意图

假设O、P两点连线或其延长线相交实际地球表面于P′点，因P′存在，可能会引起S和P不连通，导致通信中断。若P′点的海拔高度为HP′，则S与D的连通性在P点不被破坏的条件为

(2)

判定点也是需要遍历的。假设遍历步进为0.1°，则第一个判定点和D点分别与球心连线夹角就为0.1°，第二个为0.2°，以此类推。若在所有的判定点上，判定点都没有破坏发射点与目标点的连通性，则认为发射点与目标点连通。已知S与D的经纬度及海拔高度信息，可以通过数学方法求得任意判定点的经纬度信息，因此，需要根据判定点的经纬度信息获得与其对应地表点的海拔高度信息HP′。

2.2 地表海拔高度的获取

为了获得任一经纬度下的地表海拔高度信息，本文选择使用SRTM3高度数据[7]。SRTM3包括多个数据文件，每个文件用经纬度信息进行命名[8]，例如，一个SRTM3文件的文件名为N33E106.hgt，它表示以北纬33°东经106°为基点的高度数据文件，其覆盖范围在平面地图上是一个矩形，矩形的横向和纵向分别为经度、纬度的1°差范围，基点是该矩形的左下角点，即N33E106.hgt包含的高度数据是以N33E106、N33E107、N34E107、N34E106为矩形的4个角的范围内的高度数据。SRTM3高度数据采用3″角度进行采样[9]，即每个高度文件在横向和纵向均有1 201个采样点，每个采样点用两字节表示高度信息，前两个字节为矩形区域左上角点的高度信息，然后按横向进行遍历，再到下一个纬度下沿横向进行遍历，以此类推。

若已知采样点的海拔高度信息，则任一经纬度下的海拔高度信息，可以选择离该点最近的采样点的高度信息进行代替[10]。为了获得更好的近似性，本文采用空间平面插值的方法来获得，即空间内任意一点在平面地图上一定是落在以4个采样点为4个角的矩形之中，找到与待求点最近的3个采样点组成一个空间平面，认为该待求点就在这3个采样点组成的平面之上。其空间平面方程可表示为

a1x+b1y+c1z+d1=0,

(3)

式中，a1、b1、c1、d1分别表示空间平面方程的参数。

将离待求点最近的3个采样点的经纬度、海拔高度信息分别代入式(1)，可得3个采样点的3维坐标信息。再将这3个3维坐标代入式(3)中，可解得3个采样点组成的空间平面方程。待求点即满足该方程，将待求点经纬度信息代入式(1)，可得到其3维坐标与海拔高度对应关系，然后，将对应关系代入式(3)中，即可解得待求点的海拔高度信息。

2.3 目标点的经纬度

发射点的位置是在地图上选定，其经度、纬度已知。另外，发射点通常是一个通信站点，因此，其海拔高度等于其发射天线距地表高度加上该经纬度下的地表海拔高度，也是已知的。假设发射点的经度、纬度及海拔高度分别是LS，BS，HS。

然后，需要得到在任何一个方向上第一个目标点的经纬度。假设该方向的方位角为A(为方便起见，假设0°≤A≤90°，其他3个象限的处理类似)，在最大通信距离为Dmax，目标点的海拔高度为HD时，发射点、地心、目标点可组成一个三角形，如图2所示。其中，O表示地球球心，S表示发射点，D表示该方向上第一个目标点，P表示线段SD上的第一个判定点，设∠SOD=θ，则根据余弦定理可得

(4)

(5)

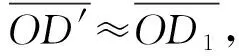
ΔB=arcsin(sinθcosA)。

(6)

假设D′在S正东方向线上的投影为D2，S在z轴上的投影为S′，则可知

(7)

(8)

(9)

所以，该方向上第一个目标点的经纬度LD、BD分别可以表示为

LD=LS+ΔL,

(10)

BD=BS+ΔB。

(11)

在确定的一个方向上其他目标点的经纬度计算方法与第一个目标点类似，只是和发射点与地心的夹角依赖于第一个目标点及相应步进。

2.4 目标点与发射点连通性判断

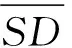
θ1=θ-0.1。

(12)

假设S、O、D三个点组成一个空间平面，由于该平面过坐标原点，因此，其平面方程为

a2x+b2y+c2z=0，

(13)

式中a2、b2、c2分别表示空间平面方程参数。若已知S及D的经纬度、海拔高度，根据式(1)，可求得S及D点的3维坐标。将两个点的3维坐标值代入式(13)，即得该平面方程。假设直线OP交地球于P1，OS交地球于S1，根据余弦定理可得

(14)

(15)

(16)

将式(13)、(15)与(16)联立求解，该三元二次方程组可以解得两组解，再结合当前方位角进行判断，可得P1的唯一三维坐标(x1,y1,z1)，再根据式(1)可解得P1的经纬度信息。

而在△SOD中，设∠OSD=β，类似地。根据余弦定理有

(17)

设∠OPS=β1，在△OPS中，则

β1=180°-β-θ1，

(18)

再根据正弦定理，有

(19)

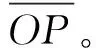
若当前判定点破坏了连通性，则认为发射点与当前目标点不连通，按照目标点中心角步进，找到当前方位角下的下一个目标点，重新对发射点与当前目标点的连通性进行判定。

若当前判定点没有破坏连通性，则按照判定点中心角步进，计算下一个判定点信息并进行连通性判定，若所有的判定点都没有破坏连通性，则认为当前目标点为当前方位角下的最远连通目标点，并记录下其经纬度信息。

根据方位角步进，找到所有方向上的最远连通目标点，在平面地图上根据经纬度信息将所有方向上的最远连通点标记出来，将相邻方向上的最远连通点相连接，所围成的区域就是射频发射覆盖区域。

3 算法实现步骤

上述基于连通性原理的射频发射覆盖范围的表示及算法，可用PC上的visual studio 2013软件实现。算法实现具体步骤如下。

步骤1 加载地图。为了使显示尽可能的详细，本文加载了17级谷歌地图，包括卫星图和地形图，可自由切换，每一级地图都包括若干个瓦片图，将这些瓦片图拼接起来，便形成了该级缩放下的完整地图，可以在地图上任选一点作为发射源并获得发射源的经纬度信息。

步骤2 加载SRTM3海拔高度数据，并使用平面插值的方法获取任一经纬度下的地表海拔高度数据。

步骤3 输入发射源位置信息，包括发射源名称、经、纬度、海拔高度或地表高度，并在地图上放置塔台图标标识当前发射源位置。

步骤4 等待添加显示区域，输入最大通信距离，目标点海拔高度，显示颜色，显示透明度，方位角步进及中心角步进。方位角步进及中心角步进是可以调节可控，步进颗粒度与算法计算量反相关，进而与程序响应时间反相关，可以根据实际需要平衡精确度与响应时间之间的关系。

步骤5 按照确定的遍历规则和相应的算法，在每个方向线上找到最远连通点，并记录下其经纬度信息。

最后，根据所获得的最远连通点的经纬度信息，在地图上将所有最远连通点标记出来，并将相邻方向线上的最远连通点相连接，将围成的区域使用所选颜色及透明度填充标记，则该区域即是以上输入条件下的射频发射覆盖区域。

4 实验结果

采用数值模拟方法和实验方法验证该算法可行性和精度。用一台PC上的visual studio 2013软件进行数值模拟，设置数据电台最大传输距离为350km，选取发射电台位置并保持不变。输入发射点的经纬度、距地表高度、最大发射距离、目标海拔高度以及方位角和中心角的步进度数，利用上述算法实现步骤计算并绘制该条件下的射频发射覆盖范围。其覆盖范围结果如图3中的深灰色区域所示，其中，中心的塔台图标标识为发射电台位置。

图3 数值仿真和实验结果

在实验上，通过多次飞机试飞对数值仿真结果进行验证。在飞机试飞实验中，保持发射电台位置不变，所选用的数据电台最大传输距离为350km，试飞飞机海拔高度为6 500m，且保持恒定进行飞行。另外，在每次的试飞过程中，试飞飞机沿固定航向飞行，飞行过程中保持与发射电台的通信，直至通信中断，记录下最后一次通信时试飞飞机的经纬度信息，即为该方向的临界点。将多次试飞的临界点在图3中标注出来，每个临界点用一个飞机图标标识。

由图3可以看出，所有飞机图标的位置都正好处在射频发射覆盖范围的边沿处，即仿真结果的阴影边界上。因此，其实验结果验证本文描述的射频发射覆盖范围的表示方法具有非常好的近似性。

5 结语

研究了数据电台组网通信系统由障碍物遮挡导致的通信中断问题。在不考虑反射、透射和衍射情况下，利用连通性原理，给出通信中断的条件。基于谷歌地图，给出了发射电台定位信息、电台最大传输距离确定、目标海拔高度条件下，在平面地图上获得发射电台射频发射覆盖区域的仿真数值方法。飞行试验结果表明，在一定精度内该方法和测试结果符合得很好。因此，本文的方法在飞机航路规划及通信站点建立位置选择等方面具有较强大的应用前景。

但是，本文使用了SRTM3高度数据表示任一纬度下的地表海拔高度信息，而SRTM3高度数据只覆盖了北纬60度至南纬60度之间的区域，因此，在该方法的应用范围上，还有待进一步扩展。