一种简化的极化码串行消除列表译码算法

李小文，李文彬

(重庆邮电大学 重庆市移动通信技术重点实验室，重庆 400065)

0 引 言

极化码(polar codes)是目前唯一被证明能够达到信道容量的新型信道编码，凭借较低的复杂度，3GPP在RAN1#87次会议上将其确定为5G增强移动宽带场景下的信道编码。极化码的结构可由P(N,K)表示，其中，N为码字的长度；K为编码中的信息比特数。由于极化码具有二元线性分组码的基本编码要素，因此，编码可通过生成矩阵乘法表示为x=uG⊗n，其中,u为原始比特序列；G⊗n为矩阵G的n次克罗内克积，x={x0,…,xN-1}为编码后的比特序列，即极化码。在编码过程中，选择K个可靠信道发送信息比特，常用数字1表示；而剩下的比特信道发送冻结比特，常用数字0表示[1]。

最常见的极化码译码方法为串行消除(successive cancellation, SC)译码,但仅适用于码长较长的情况。随后，最大似然(maximum-likelihood, ML)译码算法被提出，由于复杂性较高，以至于仅适用于极短码长的极化码。为了减小SC译码和ML译码纠错性能之间的差距，Tal和Vardy提出使用串行消除列表(successive cancellation list, SCL)译码算法进行极化码译码，主要通过存储更多条可能的译码路径来确保译码纠错性能；其次，陈凯等提出使用循环冗余校验(cyclical redundancy check, CRC)码与极化码级联，通过牺牲一定的码率，在SCL译码结束后使用CRC校验从而提升译码性能。结果显示,在某些情况下其译码性能甚至与低密度奇偶校验码相当，且随着存储路径数目的增加其译码性能甚至接近于ML译码；随后，Seyyed等提出使用码树来表示极化码的译码过程，将其看作是从码树上根据相应的路径度量值进行路径选择的过程。从码树上每层保留的路径数目来看，SCL译码算法是宽度优先译码算法，但其译码过程中存在着大量的冗余计算[2]。为减少SCL译码所需的时间步数，本文在Fast-SSC译码算法基础上提出对SCL译码树中特殊节点的简化，用于识别和消除冗余计算。

特别地，在传统SCL译码算法中对于特殊节点：Rate-1(信息比特)节点、Rate-0(冻结比特)节点和Rep(混合比特)节点其译码所需的时间步数分别为3Ns-2，2Ns-2和2Ns-1，其中，Ns=2s指码长，s指译码树中当前阶段的标号，而简化后的SCL译码算法所需的时间步数分别为min(L-1,Ns)，lbNs和lbNs+1，其中，L指搜索宽度，也称存储路径数目。通过仿真和实验结果分析，在保证纠错性能的前提下，简化后的SCL译码算法显著降低了传统SCL译码算法整个译码所需的时间步数。

1 SC译码和SCL译码

1.1 SC译码

在极化码中，基于串行消除译码算法可以表示为二叉树的遍历。图1a为P(8,4)的极化码结构图，其中，冻结比特用灰色表示，信息比特用黑色表示。转化为相应的译码树如图1b，其中，白色节点对应于冻结比特，黑色节点对应于信息比特，灰色节点表示组合2个比特的级联操作。SC译码算法从根节点开始，采用深度遍历的方式对二叉树进行遍历，从而译码。

图1 极化码的结构图和译码树Fig.1 Polar codes structure diagram and decoding tree

各个节点的消息传递如图1b，软消息α包含从父节点传递给子节点的对数似然比值(log-likelihood ratio, LLR)，而从子节点传给父节点的为硬判决消息值β，且第i位左边软消息αl和右边软消息αr的值通过如下公式计算

(1)

(2)

而第i位的硬判决消息值β通过(3)式计算，其中，⊕表示按位异或，i<2s-1用于区分左右子节点。

(3)

随后，文献[2]提出了快速简化串行消除译码(fast simplified successive cancellation, Fast-SSC)，将其译码树分为4种特殊节点进行分别处理，避免遍历整个译码树，从而简化了SC译码，如图2。图2中，白色圆圈是Rate-0节点，其叶子仅包含冻结比特；而黑色圆圈为Rate-1节点，其所有叶子均为信息比特；白色三角形表示Rep节点，只有最右边的叶子节点是信息比特；正方形表示SPC节点，即除了最左边的叶子节点都为信息比特。其中，所有的叶子节点为Rate-0或Rate-1节点，且SPC节点和Rep节点在s=1阶段相同。

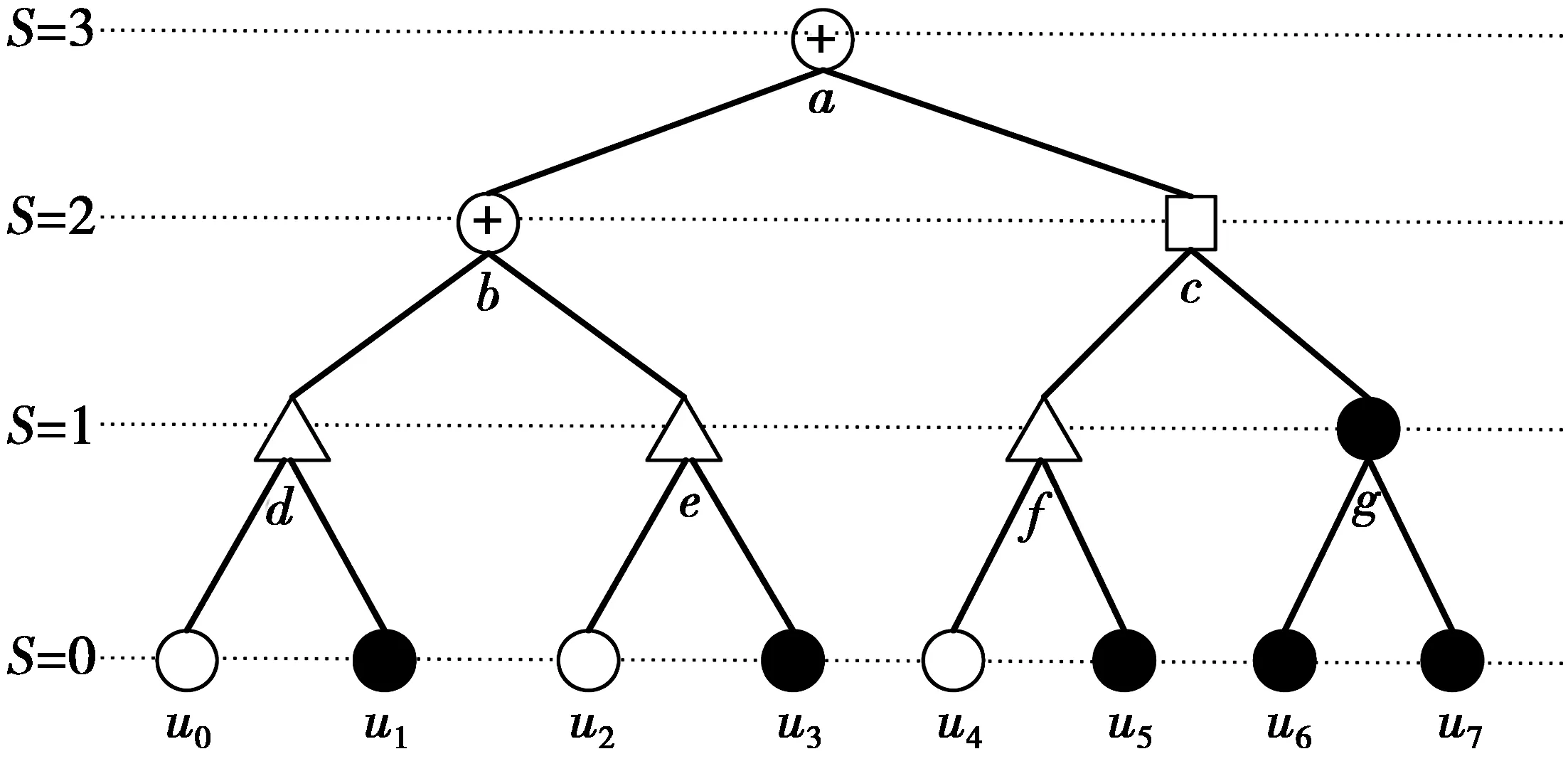
图2 Fast-SSC译码树Fig.2 Fast-SSC decoding tree

1.2 SCL译码

为了提高中等码长的纠错性能，文献[3]提出了串行消除列表译码算法。在每层估计一个比特时，其可能值0和1都必须被考虑，所以在每次估计产生的2L个候选者中，都会有一半被舍弃，剩下的L个候选者被存储，因此，SCL译码等价于对L个SC译码的并行搜索，其中，L为搜索宽度。因此，定义了选择路径的标准，即路径度量值(path metrics, PM)。将它与每条路径相关联，并在每次估计时被更新，且PM值计算公式为

(4)

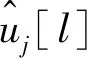
(5)

2 简化的SCL译码

基于对译码树节点分类的思想，在确保纠错性能相同的情况下，分别对SCL译码树的Rate-1节点、Rate-0节点和Rep节点做简化处理，并对其路径度量值PM重新计算，使得PM仅依赖于各自节点的译码树顶部的LLR，从而避免对整个二叉树遍历。当译码过程中遇到特殊节点时，用简化的节点去代替原来译码树的节点，从而减少了SCL译码所需的时间步数。

2.1 Rate-1节点

对于Rate-1节点简化的思想来自文献[5]中的List-SD译码，为了证明SCL译码列表大小和所需比特估计的最大数目相关，对SCL译码树的Rate-1特殊节点提出一种新的假设。

在不影响任何纠错性能的前提下，能够以min(L-1,Ns)个时间步数译码长度为Ns=2s的Rate-1节点，并且在路径l上Rate-1节点的路径度量值为

(6)

以下通过2部分证明假设，首先证明路径度量值的计算，再证明所需时间步数的假设。

2.1.1 采用归纳法证明路径度量值的计算

对于Ns=2的译码树，左右子节点的LLR如下，为避免混淆，暂时将路径l的标记先从(6)式中省略。

(7)

(8)

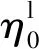
ln(1+e-η0α0)+ln(1+e-η1α1)

(9)

即(9)式等于(6)式。因此，(6)式的PM计算对于Ns=2的译码树成立。

现假设(6)式PM的计算对于长度为2s-1的译码树成立，则通过(2)—(4)式可得2个长度为2s-1的Rate-1节点的左、右PM为

(10)

(11)

对于译码树中的s阶段的任何节点来说，可将第i个比特和第i+2s-1个比特配对，并将其视为Ns=2的极化码。因此，将(10)式和(11)式中的比特配对，并当做长度为2的2s-1型的Rate-1节点的极化码，通过(9)式表示2s-1型的总和为

(12)

(12)式等于(6)式，即(6)式其PM值的计算对于Ns=2s-1的译码树成立，则对于Ns=2s也成立。因此，证得(6)式对于Rate-1节点路径度量值的计算。

2.1.2 现通过反证法证明所需时间步数的假设

为证明提出的假设，不妨设PMi和对数似然比值αl有如下排序，即

PMi1≤PMi1+1,0≤l≤L-1

(13)

(14)

即在第i步时，第l+1处的PM大于等于第l处的PM；在路径l上，第i+1处的LLR大于等于第i处的LLR。

因此，假设在第L-1处通过不同的判决值将路径l分割成2条路径，相应的PM为

(15)

(16)

(17)

(18)

因此，(17)式可通过(18)式得

(19)

单独分析第ω步的PM可得

PML-1vv

(20)

由于0≤ω≤L-2，因此，ω有L-1个值可以选择，那么对于分割路径l，(20)式的路径p表示其比特序列的所有比特与对应的LLR的硬判决一致，则至少有L个比特序列其PM比PML-1q值更小，所以L≤p。然而p

换句话说，当L-1

因此，通过上述2部分证明了Rate-1节点路径度量值的计算和时间步数的假设。

2.2 Rate-0与Rep节点

对Rate-0节点和Rep节点的简化译码所需的时间步数分别为lbNs和lbNs+1，并且对于长度为Ns=2s的Rate-0节点和Rep节点的路径度量可以分别计算为

(21)

(22)

(21)—(22)式中：αi为Rep节点的父节点传来的LLR；η2s-1为Rep节点树中信息比特的判决值的变形。其证明方法同Rate-1节点类似，不再累述。

3 性能仿真结果及分析

3.1 纠错性能

由于码率较大时存在的信息比特节点更多，编码长度Ns更大，所以，为验证简化后的SCL译码算法的纠错性能往往取min(L-1,Ns)≫2，使得搜索宽度L和码长的取值也较大。因此，根据3GPP38.212协议取码长数目为1 024，信息比特数目为860，分别采用SC译码、Fast-List译码以及SCL译码和简化的SCL译码。为尽可能的保证可靠性，对于SCL译码与简化的SCL译码其搜索宽度值L取128，且都与长度为32的CRC级联。因此，获得的误码率(bit error rate, BER)和误帧率(frame error rate, FER)的曲线如图3和图4所示。

图3 BER性能比较Fig.3 BER performance comparison

图4 FER性能比较Fig.4 FER performance comparison

显然，当信噪比从4 dB开始Fast-List译码的误码率与误帧率相对其他译码算法都较高，从而导致Fast-List译码的纠错性能损失，且随着信噪比的增加这种趋势越明显。而简化后的SCL译码仍与SC译码和传统的SCL译码保持较好的纠错性能。因此，表明简化后的SCL译码算法与传统的SCL译码算法在纠错性能方面相当。

3.2 简化处理与时间步数

下面通过举例分析SCL译码算法的简化处理。图5表示P(2,2)的SCL译码过程，由于SCL译码过程可以看做L条并行的SC译码，所以将其SC译码树也给出，便于分析和比较。

但按照SCL译码算法的简化处理，对于节点v在进行简化的SCL译码时判定为Rate-1节点且s=1，则根据公式(6)得

(23)

图5 P(2,2)的SCL译码过程Fig.5 SCL decoding process of P(2,2)

对于SCL译码算法的时间复杂度可以通过译码码字所需的时间步数来表示。假设所有可并行化的指令都在一个时钟周期内执行，则译码一个码字所需的时间步数可以计算为

TSCL=2Ns+K-2

(24)

(24)式中：K为信息比特的数目；K=Ns时译码Rate-1节点所需的时间步数为3Ns-2；K=0时译码Rate-0节点所需的时间步数为2Ns-2；由于Rep节点中包含1个信息比特，所以，K=1，因此，译码Rep节点所需的时间步数为2Ns-1。图2中，对于P(8,5)且L=2的二叉树，分别采用传统的SCL译码和简化的SCL译码对其整个译码所需的时间步数计算如下。

1)传统SCL译码所需的时间步数为

Ns=8,K=5，2Ns+K-2=19

(25)

因此，整个译码共需要19个时间步数完成。

2)简化的SCL译码所需的时间步数如下。

①对于正常节点a，b和c的关系为a→b，a→c，b→d，b→e，c→f，c→g都需要1个时间步数；

②对于节点d，e和f，都为Rep节点且Ns=2，其所需的时间步骤都为lbNs+1=2；

③对于Rate-1节点g，s=1，Ns=2s=2则所需时间步数为min(L-1,Ns)=1。

因此，简化的SCL译码总共需要13个时间步数，相对传统的SCL译码算法其所需的时间步数减少了6个。表1展示了不同译码方式每个节点所需的时间步数。

在实际译码中，时间步数还得根据自身的编码结构来确定，表2展示了对于Eb/N0=2 dB，N=2 048的极化码在不同的速率、不同列表大小下进行传统SCL译码和简化的SCL译码所需的时间步数。

表1 不同译码算法下的不同节点译码所需的时间步数

表2 各个译码算法在不同情况下的译码所需的时间步数

由表2可知，传统的SCL译码所需的时间步数仅与码率有关，而简化后的SCL译码所需的时间步数与列表大小L正相关，并且码率Rate较大时信息比特节点更多，编码长度更大，译码所需的时间步数也更多。综上，简化后的SCL译码所需的时间步数相对于传统的SCL译码较少。

4 结束语

在极化码的译码方面，本文对传统SCL译码算法的译码树进行了简化剪枝研究，通过确定3个特殊节点：Rate-1节点、Rate-0节点和Rep节点，证明对它们路径度量值的简化计算不会改变传统SCL译码的纠错性能，并且使得其译码所需的时间步数从传统的3Ns-2分别降为min(L-1,Ns)，lbNs和lbNs+1。最后，通过仿真和实验结果表明：在保证纠错性能的前提下，简化后的SCL译码算法显著降低了传统SCL译码算法整体译码所需的时间步数。