一种改进重采样的粒子滤波盲分离算法
2019-09-05林晓梦
林晓梦,高 勇
(四川大学 电子信息学院,成都 610065)
0 引 言
近年来,随着通信与电子技术的发展,盲信号处理技术[1]在军事抗干扰、移动通信、无线电测向定位、生物医疗、目标检测与跟踪等领域有着广泛的应用前景。通信混合信号的盲分离[2]是20世纪90年代发展起来的一种面向非高斯信号处理的新兴数据处理方法。它的基本思想是在缺乏信道和信号统计特性等先验知识的情况下,仅通过观测到的信号恢复出源信号。
粒子滤波和逐幸存路径处理[3]是目前盲分离的2大主流算法,诸多学者都对其进行了深入的研究。20世纪50年代,Hammersley等[4]提出的序贯重要性采样思想是粒子滤波算法的由来。随后,Doucet和Godsill从理论上证明了粒子滤波算法出现粒子退化的必然性。1993年,Gordon等[5]提出在递推过程中重新抽样,可有效避免粒子退化,奠定了粒子滤波算法的基础。2006年,Liu和Li等[6]建立了混合信号的状态转移模型,正式将粒子滤波算法应用到同频混合信号的单通道盲分离中。2016年,刘沛和邵怀宗[7]提出粒子筛选改进算法,降低了算法计算量,但该算法需将估计出的信道参数作为已知变量来展开符号估计。为提高盲分离的抗干扰能力,2014年,王娇等[8]提出小波分解结合独立分量分析的单通道盲分离抗干扰方法,降低了噪声对系统性能的影响并有效减少了计算量。2015年,朱行涛等[9]提出基于跳频信号短时平稳的二阶特征窗盲分离抗干扰方法,但该方法包括分离和提取两部分,计算较复杂。针对粒子退化问题,学者们提出了随机重采样、残差重采样、系统重采样和分层重采样等几种经典重采样算法。2011年,代芳等[10]对上述几种重采样的粒子滤波算法进行了仿真分析。2012年,李科和徐克虎[11]提出了聚类核函数平滑采样的粒子滤波,基本解决了粒子退化问题且可在一定程度上保持粒子的多样性,但是聚类的个数及门限需要根据实际信噪比情况进行设置和调整。2015年,苗少帅和周峰[12]提出通过迭代无迹Kalman滤波融入最新观测信息,生成粒子滤波的重要性密度分布,从而提高采样质量,但实时性不高。
分析几种经典重采样算法可知,随机重采样算法最简单直接,且基本解决了粒子退化问题,其基本思想是每一步都从[0,1]按均匀分布产生一个随机值与累加权比对,由此,找出权重较大的粒子复制到新粒子集中。但是该方法每次找出的仅是局部权重较大而不一定是全局权重最大的粒子。针对这一问题,本文提出一种新的改进的重采样算法。假设粒子滤波算法中粒子个数为N个,迭代一定次数后粒子退化,进行重采样。首先找出权重最大的粒子,将该粒子复制到新的粒子集中(复制次数由该粒子权重占总权重的比例决定),接着按照残差重采样思想将该粒子的权重更新为“剩余权重”,以上步骤重复次数根据粒子退化程度确定,然后将N个粒子权重归一化,再用传统的随机重采样算法复制少量粒子,补齐N个,完成重采样。文章第3节的仿真实验论证了在运用粒子滤波算法进行盲分离时,所提改进重采样算法在近似计算复杂度下误码性能优于随机重采样算法约1 dB。
1 粒子滤波算法的基本原理
1.1 粒子滤波原理
粒子滤波(particle filter, PF)方法又称序列蒙特卡罗(sequential Monte Carlo, SMC)方法,它提供了一种在非高斯、非线性模型下计算未知变量的后验概率分布的有效途径。基本思想是对未知变量的后验概率分布进行蒙特卡罗采样,调整每个采样点的权重,逼近最终的概率分布函数[4]。每个采样点称为一个粒子,当粒子数足够多时能逼近任意复杂的概率分布函数,粒子滤波的估计就达到了最优贝叶斯估计的效果,但是粒子数的增多也带来了对应着计算量的大幅增加,因此,在实际计算中粒子数的选取需根据具体情况综合考虑。
将待要估计的未知变量(又称状态)记为xk,初始分布为p(x0),观测数据为yk,状态转移概率为p(xk|xk-1),k≥1,边缘概率为p(yk|xk),k≥1,用x0:k={x0,…,xk}表示从时刻0到时刻k的状态,y1:k={y1,…,yk}表示从时刻1到时刻k的观测数据。那么,粒子滤波算法的目标就是实时递归地估计未知变量xk的后验概率分布p(x0:k|y1:k)、相关统计特性以及未知变量函数fk(x0:k)的期望I(fk)。
1.2 粒子滤波算法
根据要待估计的未知变量xk(又称状态)和观测数据yk建立状态转移方程和观测方程为
(1)
(1)式中,vk和nk分别为状态转移噪声和观测噪声。状态转移概率p(xk|xk-1)和边缘概率p(yk|xk)可分别通过状态转移方程和观测方程得到。
若已知状态的初始概率密度函数为p(x0|y0)=p(x0),则目标的后验概率密度p(xk|y1:k)可通过2步递推得到
(2)
(3)
(2)式为预测公式;(3)式为更新公式。

(4)
(4)式中,q()是重要性函数,特别地,当重要性函数为先验分布时,有
(5)
(6)
那么,k时刻的后验概率密度可表示为
(7)
(7)式中,δ()为狄拉克函数。

2 粒子退化重采样
重采样算法是降低粒子多样性匮乏的一种有效方法,其基本思想是对由粒子和相应权重表示的概率密度函数进行重新采样,增加权重较大的粒子数,同时减小权重较小的粒子数。
为衡量粒子匮乏程度,定义“有效粒子数”Neff为
(8)
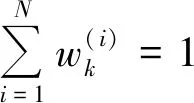
(9)

2.1 随机重采样
随机重采样是目前最常用的重采样算法之一,因其最简单直接,且基本解决了粒子退化问题。随机重采样的步骤如下[8]。
首先定义累加权λi为
(10)

2.2 改进的重采样
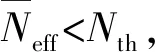
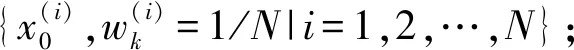
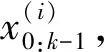


(11)
(12)

2.3 基于改进重采样的粒子滤波盲分离
粒子滤波盲分离的基本思想是将待估计的2路同频混合信号的符号序列和时延、频率、幅度、相位等调制参数作为状态变量进行建模,用粒子滤波算法估计出这些变量的后验概率分布,则符号序列后验概率分布的期望就是最终的分离结果。
考虑对同符号速率且同调制方式的2路信号构成的混合信号进行分离,首先将待估计信号的符号序列和调制参数作为状态变量建立状态转移模型,状态方程为
(13)
(13)式中,

(14)
(14)式为L×L移位矩阵,L=L1+L2为信道串扰有效阶数,L1,L2分别为2路信号的串扰长度,Φk=[fk-L1+1,…,fk+L2]为符号对向量,φk=(a1,k,a2,k)为k时刻符号对,dk=[0,…,0,fk+L2]为包含最新到达符号对φk+L2的更新向量,Θk={h1,k,h2,k,τ1,k,τ2,k,Δω1,k,Δω2,k,θ1,θ2}为信号参数集,uk为参数扰动,Θk=f(Θk-1,uk)为当前时刻参数。

(15)
(15)式中,Φ和Θ相互独立,可推导出粒子权重更新公式为
(16)
(17)
(18)
(17)式为参数Θ的最小均方误差估计值,(18)式为符号序列Φk-D的最大后验概率估计值。
综合上述,基于改进重采样的粒子滤波盲分离算法步骤可归纳如下。



步骤4符号估计:根据 (18) 式进行符号估计,若符号序列未估计完,令k=k+1,回到步骤1继续迭代,直至估计出全部符号序列。
3 实验仿真与分析
考虑2路相同符号速率下的二进制相移键控(binary phase shift keying,BPSK)调制信号的混合信号,实验对基于改进重采样和随机重采样的粒子滤波盲分离分别进行了仿真,并对其结果进行了对比分析。仿真参数设置如下(以下所有参数下标1,2分别表示2路信号):采用根升余弦成形滤波器,滚降系数0.35,噪声为高斯噪声,信号幅度h1,k=h2,k=1,频偏Δw1=Δw2=0,相偏θ1=π/4,θ2=π/16,固定时延τ1,k=0.55T(T为符号周期),τ2,k=0.1T,2倍采样。分离时取L1=L2=2,故L=L1+L2=4,(L是等效滤波器的总响应持续时间),粒子滤波平滑长度D=2,粒子数N=200,有效粒子数阈值Nth=0.75N(取ε=0.75),符号数M=3 000。
混合信号信噪比为8 dB时,分别采用改进重采样和随机重采样粒子滤波算法进行盲分离仿真,各调制参数(幅度、相位、时延)的收敛曲线依次由图1—图3所示。

图1 不同重采样算法下的幅度估计曲线Fig.1 Amplitude estimation curves of different resampling algorithms
图1分别给出了采用随机重采样和本文提出的改进重采样算法进行粒子滤波盲分离时2路信号的幅度估计曲线,可以看出,2种算法均成功将2路信号分离,且均在经过大约200个符号后收敛,对比图1a和图1b可见,改进重采样算法下的幅度估计曲线略微更接近于仿真预设幅度h1,k=h2,k=1 。

图2 不同重采样算法下的相位估计曲线Fig.2 Phase estimation curves of different resampling algorithms

图3 不同重采样算法下的时延估计曲线Fig.3 Delay estimation curves of different resampling algorithms
图2分别给出了采用随机重采样和本文所提的改进重采样算法进行粒子滤波盲分离时2路信号的相位估计曲线,可以看出,2种算法均成功将2路信号分离,对比图2a和图2b不难看出,随机重采样算法下估计曲线经过大约400个符号后收敛,改进重采样算法下估计曲线在大约150个符号后收敛,且改进重采样算法下的相位估计曲线明显更接近于仿真预设相位θ1=π/4,θ2=π/16。
图3分别给出了采用随机重采样和本文提出的改进重采样算法进行粒子滤波盲分离时2路信号的时延估计曲线,可以看出,2种算法均成功将2路信号分离,且均在经过大约100个符号后收敛,对比图3a和图3b可以看出,2种重采样算法下的时延估计曲线相差无几。
根据图1—图3,对比2种不同重采样算法粒子滤波盲分离中对同一参数的收敛曲线,2路信号的幅度、相位、时延均表现出一定的差异,说明2路信号已被成功分离,且各参数都在经过一定符号后收敛到稳定值。由此得出,随机重采样粒子滤波算法和本文提出的改进重采样粒子滤波算法都能有效实现混合信号的单通道盲分离,且改进重采样的粒子滤波算法相较随机重采样粒子滤波算法而言,参数估计的收敛速度略快,准确性也更优。对参数估计的收敛速度和准确性均略优于随机重采样粒子滤波算法。
沿用上述仿真参数,将平均误符号率作为盲分离性能的评价指标,混合信号的信噪比设置为变量,对不同信噪比条件下的混合信号分别采用改进重采样和随机重采样粒子滤波算法进行盲分离,经过大量仿真实验得到平均误符号率性能对比曲线如图4所示。

图4 不同重采样算法的粒子滤波盲分离性能对比图Fig.4 Particle filter blind separation performance comparison chart of different resampling algorithms
由图4可知,采用改进后的重采样粒子滤波算法进行盲分离时,在计算量相差无几的情况下较传统的随机重采样粒子滤波盲分离误码性能略优约1 dB,由此可得出,本文提出的改进重采样的粒子滤波盲分离算法是有效的。
为了验证本文所提算法的普遍性,将粒子数选取为N=300,其余参数沿用不变的条件下,重新进行仿真实验,得到改进重采样和随机重采样粒子滤波盲分离的平均误符号率性能对比图如图5。

图5 不同重采样算法的粒子滤波盲分离性能对比图(N=300)Fig.5 Particle filter blind separation performance comparison chart of different resampling algorithms(N=300)
图5是增加粒子数时得到的盲分离性能对比图,比较图4和图5可知,当粒子数增大时,2种算法的误码性能都有略微提升,但这是以计算量的增加为代价的,工程应用中需根据实际情况折中考虑粒子数的选取。并且由图5可知当粒子数改变时,本文所提算法相比随机重采样算法仍有约1 dB的性能提升。实验仿真结果表明,在盲分离应用中,本文提出的改进重采样粒子滤波算法较随机重采样粒子滤波算法性能提升了约1 dB,且该算法具有一定普遍性。
4 结 论
在单通道混合信号盲分离中,针对粒子滤波算法的粒子退化问题,本文简要介绍了粒子滤波算法的原理,提出一种改进重采样的粒子滤波算法。实验仿真结果表明,本文提出的改进重采样粒子滤波算法用于同调制混合信号盲分离时的误码性能相较随机重采样算法提高了约1 dB,且所提算法对信号参数估计的收敛速度更快、准确性更高。但对于粒子滤波算法的另一难题“复杂度”,本文提出的改进重采样粒子滤波算法计算量与随机重采样粒子滤波算法相当,也就是说计算复杂度没有大幅明显降低,这也是今后仍需进一步深入研究的问题。
